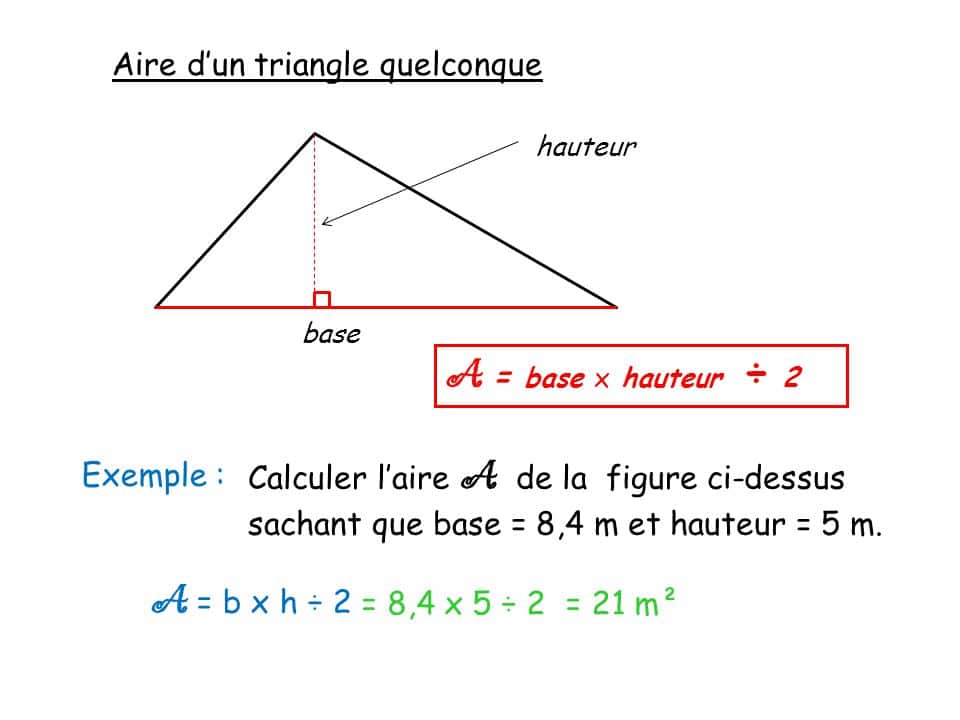
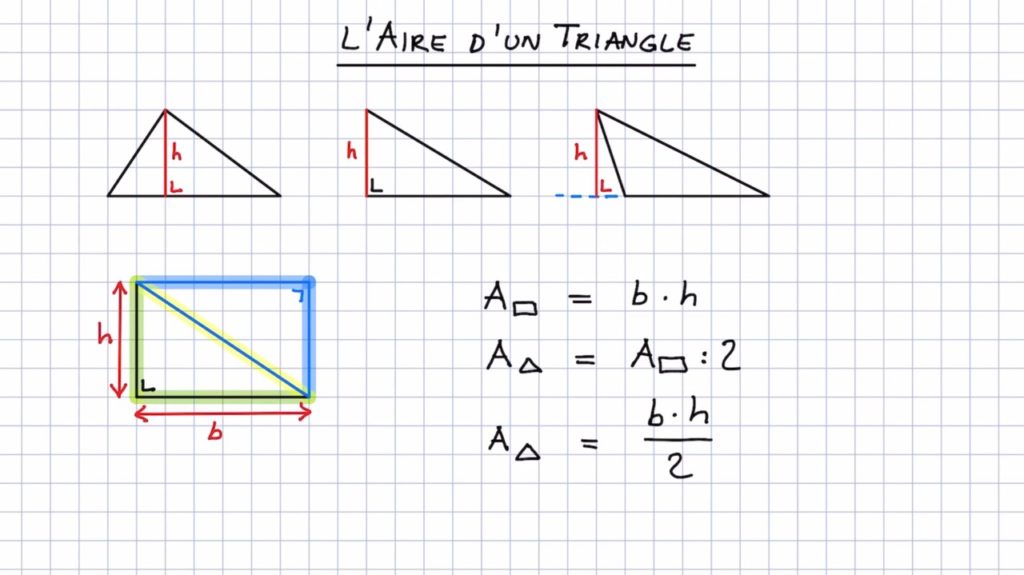
Calculer l'aire (de la surface) d'un triangle quelconque Un triangle est une figure plane qui possède 3 côtés. Soit un triangle de base B et de hauteur h. Son aire est égale à la moitié du produit la longueur de sa base par la hauteur issue du sommet opposé à cette base, soit : Valeur de base: Valeur de la hauteur : Principe de calcul de l'aire d'un triangle quelconque En traçant une hauteur d'un triangle quelconque (droite passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet) , on décompose ce triangle en deux triangles rectangles.
Comment Calculer L Air D Un Triangle Isocele Communauté MCMS™.
Méthode 1 Calculer l'aire d'un triangle en utilisant la base et la hauteur Télécharger l'article 1 Trouvez la base et la hauteur d'un triangle. Par définition, la base d'un triangle est le côté sur lequel il repose. La hauteur est la ligne qui part du sommet opposé à la base et qui se termine sur la base, mais à ange droit. L'aire d'un triangle quelconque = (Base du triangle x hauteur du triangle)/2. Un triangle quelconque est un triangle qui n'est pas rectangle. Formule de calcul de l'aire d'un triangle Calculer l'aire, c'est mesurer sa surface. : Hauteur (h) (en unité : cm, m…) : Aire du triangle (en unité ²) : Exemple de calcul d'une aire d'un triangle : ABC est un triangle de base b = 3 cm et de hauteur h = 5 cm Aire A du triangle ABC = (b x h )/2 = (3 x 5)/2 = 15/2 = 7,5 cm² Cas du triangle rectangle : calcul de l'aire d'un triangle rectangle AB = hauteur = h BC = base = b L'aire d'un triangle peut être calculée en le décomposant en deux triangles rectangles. Si le triangle est rectangle, il est immédiat que son aire est où a est la longueur d'un côté différent de l'hypoténuse et h la longueur de la hauteur issue de ce côté.
Périmètre et aire de polygones MathZkool
Comprendre et retenir comment calculer l'aire d'un triangle quelconque. L'aire d'un triangle quelconque peut être calculée à l'aide de la formule : A = b a s e × h a u t e u r 2 Base et hauteur d'un triangle Le triangle A est représenté ci-dessous (toutes les longueurs sont en cm) : Calcul de l'aire d'un triangle quelconque L'aire du triangle = 10 × 5 2 = 25 c m 2 Aire d'un triangle isocèle Calcul de l'aire du triangle par la base et la hauteur. Le triangle calculé par sa base et sa hauteur. Longueur de la base B : Hauteur H : Unité : Nombre de chiffres après la virgule : Surface du triangle : 0,50 m 2. 3. notion Faire les exercices Si c désigne la longueur d'un côté d'un triangle et h la hauteur relative à ce côté, l'aire de ce triangle est égale à (c × h) ÷ 2. Aire du triangle quelconque ABC : (AH) est la hauteur relative à [BC]. BC = 5 cm ; AH = 4 cm. L'aire du triangle ABC, en cm 2, est égale à : BC × AH2 = 5 × 4 2 = 10

Comment calculer l'aire d un triangle quelconque YouTube
Où l'on démontre que si b est la longueur d'un côté d'un triangle et h celle de la hauteur relative à ce côté, alors l'aire du triangle est A = 1/2 b x h. Créé par Sal Khan. Questions. Conseils et remerciements. Comment calculer l'aire d'un triangle quelconqueMerci de s'abonner à notre chaîne YouTube https://bit.ly/32K4jpMDans ce tuto le Papillon matheux on va découv.
Aire du triangle par hauteur et base. Triangle area = (height * base) / 2. L'aire du triangle est également possible de calculer de différentes manières avec les angles et les longueurs du triangle. Aire du triangle par trois côtés. Triangle area = 1/4 * √ ( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c) ) Aire du triangle par. aire = 0,5 × a × b × sin (γ) Deux angles et le côté entre ces angles (A-C-A) En l'occurrence, ils existent différentes formules pour calculer l'aire d'un triangle. Par exemple, vous pouvez utiliser la trigonométrie ou la loi des sinus 🇺🇸 : Aire = a² × sin (β) × sin (γ) / (2 × sin (β + γ))

Lernen Ecke aus calculer l aire d un triangle rectangle Strich Ernst einfach
Comment calculer l'aire d'un triangle ? Quelconque ? La formule étudiée ici est valable pour tous les triangles, quelconques, isocèles, équilatéraux, rectang. 1) l'aire du triangle = 4 × 6 × sin (70) ÷ 2 l'aire du triangle = 11.28 2) DF = √ (DE² + EF² − 2×DE×EF×cos (70)) DF = √ (4² + 6² − 2×4×6×cos (70)) DF = √ (16 + 36 − 16.416966879632) DF = 5.97 cm d'où la hauteur issue de E = 11.28 × 2 ÷ 5.97 = 3.78 3) et les angles : β = 39° γ = 71°




