Ce formulaire de développement en séries recense des développements en séries de fonctions pour les fonctions de référence (pour la plupart, des séries entières, et quelques séries de Laurent).Elles sont données avec indication du domaine de convergence (le rayon de convergence pour les séries entières) dans le champ complexe ou réel. La notation (,) représente la boule ouverte. Retrouvez aussi tous nos exercices de développements en série entière. Découvrez toutes nos fiches aide-mémoire : Le vocabulaire des graphes; Les formules des surfaces usuelles; Formulaire : Toutes les formules à connaitre sur les vecteurs; Les fonctions usuelles; Les limites usuelles; Les différents types de suites en mathématiques

Dévellopement en séries entières (programme mViewer GX Creator Ndless Nspire)
Cours sur le rayon de convergence d'une série entière. On appelle série entière toute série de fonctions de la forme ∑nanzn ∑ n a n z n où (an) ( a n) est une suite de nombres complexes et où z ∈C z ∈ C. Lemme d'Abel : Si la suite (anzn 0) ( a n z 0 n) est bornée, alors pour tout z∈ C z ∈ C avec |z| <|z0| | z | < | z 0 |, la. Développements en séries entières usuels Ilyatroisdéveloppementsensériesentièrestrèsimportants(ceuxencadrés),etàpartirdesquelsonpeut. En mathématiques et particulièrement en analyse, une série entière est une série de fonctions de la forme . où les coefficients a n forment une suite réelle ou complexe. Une explication de ce terme est qu' « au XVII e siècle, on appelle fonctions entières des fonctions définies sur tout le plan complexe.On parle de séries entières lorsqu'elles s'expriment sous forme de séries en. Développement en série entière. Soit I I un intervalle ouvert contenant a a, f: I → R f: I → R. On dit que f f est développable en série entière en a a s'il existe r > 0 r > 0 tel que ]a−r,a+r[] a − r, a + r [ soit contenu dans I I , et une suite de réels (an) ( a n) telle que.
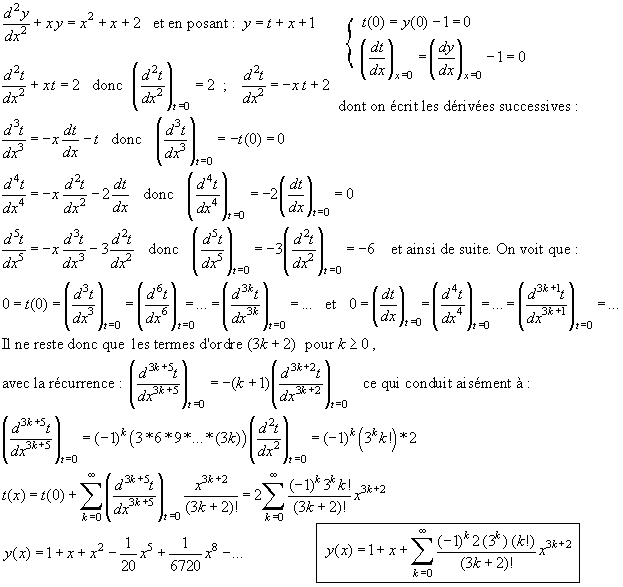
serie entiere et equation diff Forum mathématiques bts analyse 67465 67465
utiliser les développements en série entière usuels, et les opérations de somme, de produit, de dérivation (voir cet exercice); pour une fraction rationnelle, on la décompose d'abord en éléments simples et on développe chaque terme (voir cet exercice); pour une fonction définie par une intégrale ou une série, on développe souvent la fonction à l'intérieur de l'intégrale ou de. Transcription de la vidéo. déterminés les quatre premiers termes non nul du développement série entière centre et 11 02 la fonction fdx égale arc tangente de 2 x donc on doit déterminer le développement en séries entières centre et 11 027 fonction arc tangente de 2x et on doit déterminer en fait uniquement les quatre premiers termes. Développement en série. Cette page d'homonymie répertorie les articles traitant de différentes notions mathématiques avec une dénomination commune. Un développement en série est l'expression d'une fonction sous forme d'une série de fonctions élémentaires. Sur un domaine donné, la fonction est égale à la série de fonctions simples. Dans cette vidéo, nous allons voir le développement d'une fonction en série entière, une condition nécessaire et suffisante pour qu'une fonction soit dévelop.

Exercices Corriges Series Entieres Série (mathématiques) Série entière
Développements usuels en série et développements limités. Logarithme. Développement de puissances. Fonctions circulaires réciproques: arcsin et arccos. Fonction circulaire réciproque: arctan. Série exponentielle. Fonctions circulaires: sin et cos. Fonctions hyperboliques: sh et ch. Formules de Taylor. en série entière autour de zéro. Exercice 13 On se propose d'obtenir le développement en série entière de la fonction tangente. Pour x 2] ˇ=2;ˇ=2[, on pose f(x) = tgx. (1) En remarquant que f′ = 1 + f2, montrer qu'il existe une suite (Pn) de polynômes à coe cients dans N telle que f(n) = Pn f pour tout n 2 N.
Chap. 09 : cours complet. 1. Rayon de convergence et somme d'une série entière. Définition 1.1 : série entière réelle ou complexe. Théorème 1.1 : lemme d'Abel. Théorème 1.2 : intervalle des valeurs positives où une série entière a son terme général borné. En déduire la valeur de, , ainsi que l'expression de en fonction de . Allez à : Correction exercice 10 Exercice 11. On définit la suite ( ) par et par la relation de récurrence ∑() Et on pose . 3 1. Montrer que | | , en déduire que le rayon de convergence de la série entière de terme général.

Développement d'une fonction en série entière LesMath
En déduire que $1/f$ est développable en série entière. Indication . Corrigé Utilisation de développements en séries entières. Exercice 38 - Régularité [Signaler une erreur] [Ajouter à ma feuille d'exos]. Dans cette vidéo on va surtout s'intéresser aux conditions qui permettent de savoir si une fonction peut s'écrire localement comme la somme d'une série entiè.




