Exercices. 1. Nombre entier ; 2. Nombre décimal ; 3. Écrire un nombre décimal ; 4. Écrire un nombre décimal ; 5. Écriture décimale d'une fraction ; 6. Nombre décimal et fraction ; 7. Comparer des nombres décimaux ; 8. Nombres et fractions ; 9. Abscisse d'un point ; 10. Abscisse d'un point ; Vidéos. 2. Calcul . Cours; Exercices. 1. Exercice n°1 Question 1 FAUX . En effet, si les points B,A et C sont alignés « dans cet ordre » (c'est-à-dire si A appartient au segment [BC], alors on aura AB AC = - AB · AC VRAI par définition VRAI A est le milieu de [BC] ssi ( AB , AC ) =p [ p ] donc ssi AB AC = AB · AC · cos ( p ) = - 2 AB = AB =- 1 Question 2

Le produit scalaire Exercices non corrigés AlloSchool
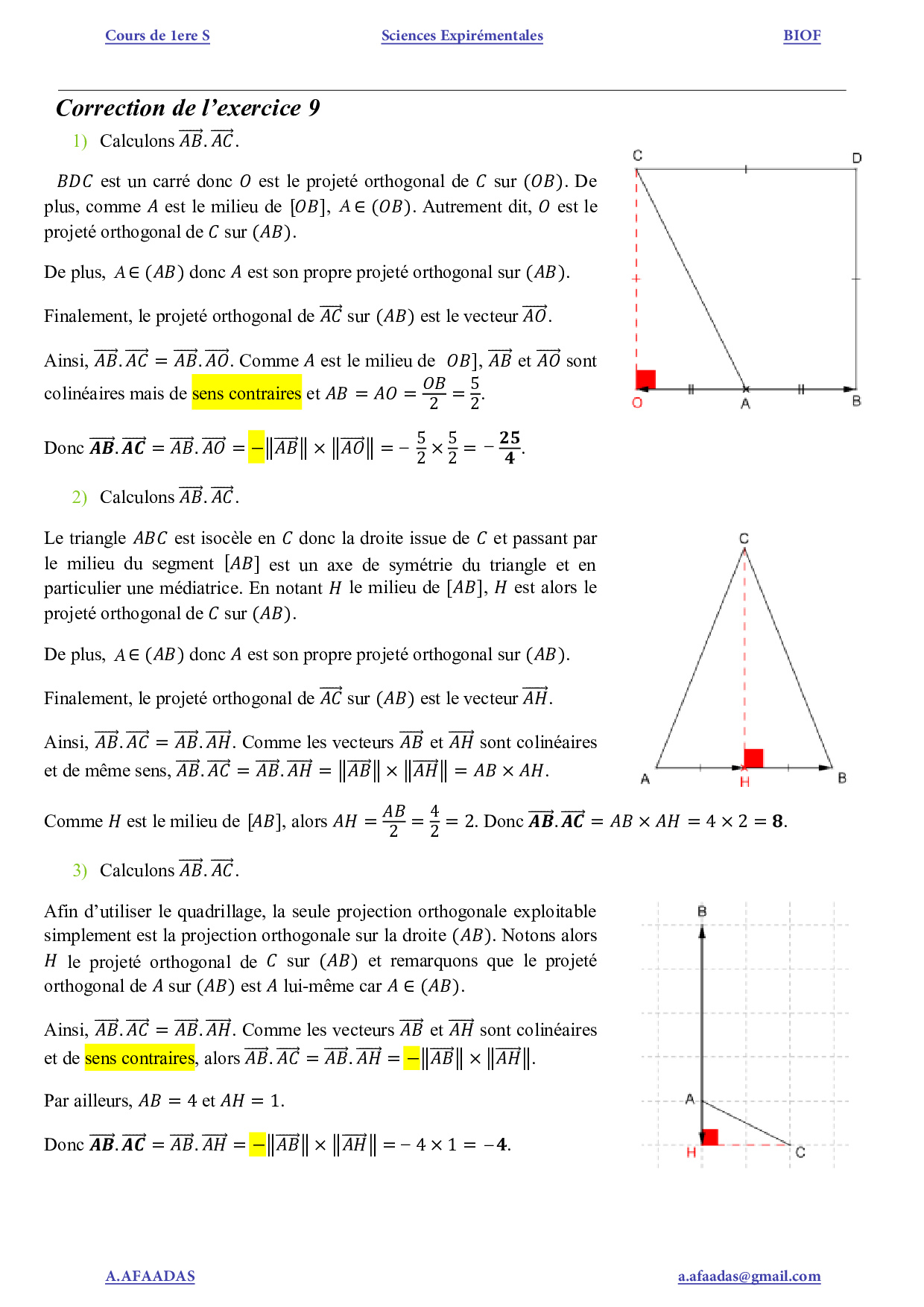
Exercices corrigés de mathématiques pour la 1S concernant le produit scalaire et ses applications. Utiles pour des révisions pendant les vacances. Exercice 2 corrigé disponible. ABCD est un rectangle, I est un point de [CD] défini comme l'indique la figure ci-dessous. 1. Démontrer que : (⃗ ID+⃗ DA)⋅(⃗ IC. 2. En déduire que : ⃗ IA⋅⃗ IB=6 et. +⃗ CB)=⃗ ID⋅⃗ IC +DA2 cos^ 1 AIB=. √5. Exercice 3 corrigé disponible. Exercices corrigés sur le produit scalaire en 1S. Au programme utilisation du produit scalaire pour calculer des angles, vecteur normal à une droite et équation de cercle. Chapitre 07 - Produit scalaire; Cours vidéo; Cours à imprimer; Exercices vidéo; Exercices CORRIGES; Contrôles CORRIGES; Chapitre 08 - Suites arithmétiques et géométriques; Chapitre 11 - Géométrie repérée; Chapitre 10 - Variables aléatoires; Chapitre 09 - Fonction exponentielle; Contact / Remerciements

Le produit scalaire Cours et exercices corrigés AlloSchool
−1). Donner les coordonn ́ees de −→ AB et −→ AC et les longueurs AB et AC. Exercice 2 Rappeler les formules de trigonom ́etrie, cosinus, sinus et tangente dans un triangle rectangle. Que vaut la hauteur dans un triangle ́equilat ́eral de cˆot ́e 1 ? que vaut son aire ? Exercice 3 a) Rappeler la relation de Chasles. b) Dans un rep`ere, on donne −→ 1re spé / Produit scalaire : 56 exercices corrigés pour vos révisions + 26 exercices de mathématiques pour les professeurs. 1) Calculer les produits scalaires suivants : ! ! OI OJ !! OI OK !! OI OB ! ! OB OA paul milan !! 2) Prouver que dans le repère (O; { ;| ) les coordonnées de B sont calculer : 3 et 2 p 3 3 , puis 2 ! ! OA AI ! ! IA IJ ! ! BK BA Exercice 3 : Sur les expressions du produit scalaire Des exercices sur le produit scalaire pour s'entraîner Pour t'entraîner et vérifier si tu as compris comment appliquer ces formules du produit scalaire, télécharger la feuille d'exercices sur le produit scalaire de deux vecteurs ici. Pour vérifier tes résultats et t'améliorer, voici le corrigé des exercices sur le produit scalaire.

Le produit scalaire dans le plan Exercices corrigés (FR) AlloSchool
Si l'un des vecteurs est nul le produit scalaire est nul et la propriété est vraie puisque, par convention, le vecteur nul est orthogonal à tout vecteur du plan. Si les deux vecteurs sont non nuls, leurs normes sont non nulles donc : Exercice 1 : calculer le produit scalaire → u.→ v u →. v → avec → u ⎛ ⎜⎝ 4 −1 3 ⎞ ⎟⎠ u → ( 4 − 1 3) et → v ⎛ ⎜⎝ −2 1 5 ⎞ ⎟⎠ v → ( − 2 1 5) Exercice 2 : calculer le produit scalaire → u.→ v u →. v → avec → u ⎛ ⎜⎝ −a b a −b ⎞ ⎟⎠ u → ( − a b a − b) et → v ⎛ ⎜⎝ a b a +b ⎞ ⎟⎠ v → ( a b a + b)
Sommaire. Calcul du produit scalaire. Démo du théorème de la médiane. Application au calcul d'un angle. Produit scalaire en créant un repère. Pour accéder au cours sur le produit scalaire, clique sur ce lien ! Pour accéder aux exercices post-bac sur le produit scalaire, clique ici ! Le produit scalaire au lycée : Cours et exercices corrigés Cours Révisions du bac Le produit scalaire au lycée : Cours et exercices corrigés Tout savoir sur le produit scalaire, niveau lycée : Définition, propriété et exercices corrigés Partager : par Valentin Strach 8 août 2022 3 minutes de lecture 3 commentaires
Le produit scalaire dans le plan Exercices corrigés (FR) AlloSchool
Exercices Définition du produit scalaire Soient E E un \R R -espace vectoriel. On appelle produit scalaire, noté \langle . | . \rangle .∣. et définie sur E \times x E \to \R E ×xE → R toute forme bilinéaire symétrique définie positive. Voici ce que cela signifie : bilinéaire : Le produit scalaire, Cours, Examens, Exercices corrigés pour primaire, collège et lycée. Notre contenu est conforme au Programme Officiel du Ministère de l'Éducation Nationale




