Taper vos données pour calculer la hauteur d'un triangle équilatéral connaissant son côté. Imprimez gratuitement des calendriers, agendas et emplois du temps (année scolaire 2023-2024) ! Editions Petite Elisabeth. Comme un triangle équilatéral est isocèle en chacun de ses sommets, chaque médiane est aussi une hauteur, bissectrice, et portée par la médiatrice du côté opposé. Ce segment partage le triangle en deux triangles rectangles symétriques dont l' hypoténuse mesure le double d'un autre côté.

Bonjour, Que vaut la hauteur dans un triangle équilaterale de côté a ? Nosdevoirs.fr
Calculer la hauteur d'un triangle équilatéral. 1) Le triangle AHB est rectangle en H, nous pouvons appliquer le théorème de Pythagore. 2) Pour c = 35 cm nous obtenons h ≈ 0,866 × 35 ≈ 30,31. Utilisez la formule de calcul de l'aire d'un triangle. La formule la plus courante est la suivante : [1] , formule dans laquelle : A {\displaystyle A} est l'aire du triangle ; b {\displaystyle b} est la longueur de la base du triangle ; h {\displaystyle h} est la hauteur associée à la base précédente. 2. Comment sont calculées les hauteurs dans le triangle équilatéral ? Pour calculer la hauteur de a dans le triangle équilatéral, la formule suivante peut être utilisée à la place de la formule plus compliquée pour les triangles généraux : Aire du triangle équilatéral. En gardant la même notation qu'au-dessus, l'aire vaut. A = \dfrac {a^2} {4} \sqrt {3} A = 4a2 3. Car la hauteur issue de la base est. h = \dfrac {a} {2} \sqrt {3} h = 2a 3. On peut aussi retrouver cette formule grâce à la formule de Héron. Découvrez notre article sur la formule de Héron.
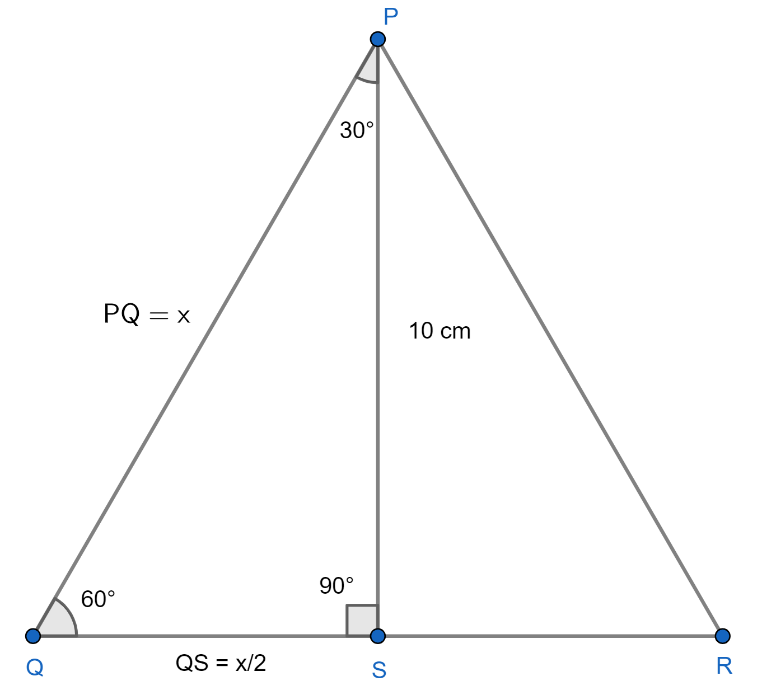
The height of an equilateral triangle is 10 cm. Its area is.\n \n \n \n \n (a) \\dfrac{100}{3
La hauteur $h$ du triangle équilatéral de côté $a=10$cm s'écrit : $h=a\dfrac{\sqrt{3}}{2}$. Donc : $h=\dfrac{10\sqrt{3}}{2}$. Ce qui donne : $$\boxed{\; h=5\sqrt{3} \;}$$ Et par conséquent, à la calculatrice, on obtient : $$\boxed{\; h\simeq8,660~\text{cm}\;}$$ hauteur d'un triangle équilatéral • Démontrer la formule h=√3/2a • Exercice classique • Seconde math jaicompris Maths 372K subscribers Subscribe Subscribed 646 48K views 4 years ago Puissance &. Calculer la hauteur d'un triangle équilatéral • théorème de Pythagore • Quatrième • Un classique ! http://www.jaicompris.com/lycee/math/. nathan transmath quatrième chapitre 16. On travaille ici dans un triangle équilatéral dont on connaît l'aire et il faut retrouver la mesure d'un côté. Exercice de mathématique de niveau seconde/première sur la résolutions d'é.
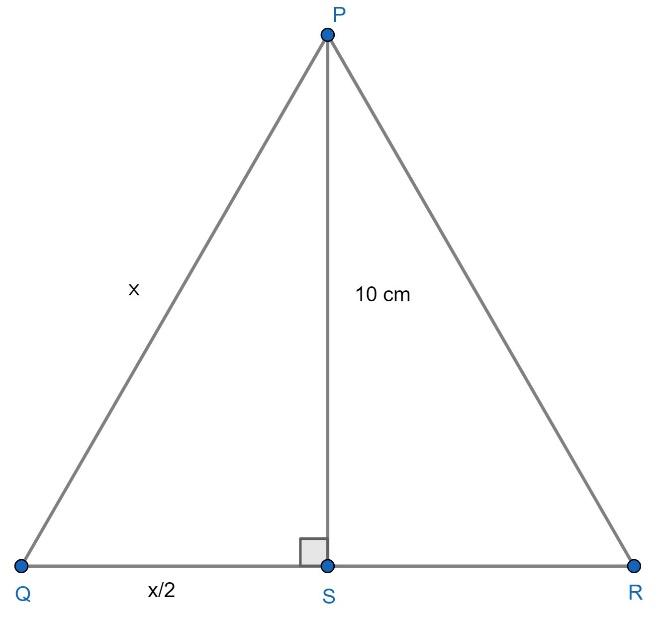
The height of an equilateral triangle is 10 cm. Its area is.\n \n \n \n \n (a) \\dfrac{100}{3
Formules. La formule pour calculer l'aire A d'un triangle équilatéral est : A = c2 4 3-√ c 2 4 3. La formule pour calculer le rayon r du cercle circonscrit à un triangle équilatéral est : r = c 3 3-√ c 3 3. La formule pour calculer le rayon r du cercle inscrit dans un triangle équilatéral est : r = c 6 3-√ c 6 3. La hauteur d'un triangle équilatéral est égale à la longueur que l'on multiplie par la moitié de la racine carrée de 3. L'aire d'un triangle équilatéral de côté a vaut a² × sqrt (3) /4 Construction d'un triangle équilatéral Etape 1 Etape 2 Etape 3 Portail des mathématiques — Les nombres, la géométrie, les grands mathématiciens. Catégories :
Hauteur du triangle équilatéral. Un triangle équilatéral est un triangle dans lequel tous les côtés sont égaux. De même, les hauteurs de n'importe quel sommet sont également égales. Tous les angles sont égaux à 60 degrés. Définition Un triangle équilatéral est un triangle qui a trois côtés de même longueur. Remarque : on code l'égalité des longueurs en utilisant le même symbole. Construction On trace un segment. Avec le compas, on reporte la longueur du segment à partir de chaque extrémité.

Exercices En Ligne Sur Les Triangles Ce2 Médiatrice Cercle circonscrit Triangles 5ème
Solution Aire AEC = 1/2 AC x DE = 1/2 Aire de ABC Aire AECB (complémentaire) = 1/2 Aire de ABC. Les triangles AEB et CEB sont égaux (congruents). Aire AEB = 1/4 Aire de ABC. TRIANGLE ÉQUILATÉRAL Triangle dont les trois côtés sont égaux (de même longueur). C'est un triangle isocèle particulier. Les trois angles sont égaux et valent 60°. Un triangle équilatéral est un triangle qui a trois côtés de même longueur.. La hauteur du triangle A BC issue de A est la droite passant par le point A et perpendiculaire à la droite (BC). Dans les deux triangles A BC ci-dessous, avec l'équerre, tracer la hauteur du triangle A BC issue de A. Appeler (h) cette hauteur et I le point d'intersection entre (h) et (BC). Propriétés.



