Primitive des fonctions usuelles : Comment trouver les primitives d'une fonction - les techniques Tableau regroupant les primitives au programme de mathématiques en Terminale S. Tout y est, vous n'avez qu'à l'utiliser en rappel, et découvrir notre forum et nos exercices pour progresser sur Mathforu. The primitive equations are a set of nonlinear partial differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations: A continuity equation: Representing the conservation of mass.

Tableau des primitives Trent Davis
u et v sont des fonctions de primitives respectives U et V Fonction f Une primitive F (déterminée à une constante près) Remarques f = u + v F = U + V f = ku (k constante) F = kU Dans la suite u est dérivable sur un intervalle I f = u' un (n ≠ -1) F = 1 n 1 un+1 selon les valeurs de n f = u' u2 In Houdini and Mantra, Primitives all have an implicit parametric space, sometimes called primitive UVs, for referring to positions on their surfaces, or other interpolations of Geometry attributes on their points or vertices. primuv Houdini 20.0 Expression functions primuv expression function Returns the value of a primitive attribute at a certain UV location. HOM equivalent hou.Face.positionAt () hou.Face.attribValueAt () hou.Prim.positionAtInterior () hou.Prim.attribValueAtInterior () hou.Surface.positionAt () hou.Surface.attribValueAt () primuv VEX function Interpolates the value of an attribute at a certain parametric (uvw) position. This function specifies the position using intrinsic primitive UVs. To use UVs stored in UV attribute, use uvsample instead.
primuv(geometry, string attribute_name, int prim_num, vector uvw)

sept heures et demie Inutile conservateur tableau primitive fonction usuelle selle Repousser en
Show that f has a primitive in U ∪ V . complex-analysis convex-analysis Share Cite Follow asked Mar 21, 2021 at 12:45 maria 21 3 It suffices to prove that U ∪ V U ∪ V is simply connected, which follows from Seifert-Van Kampen's theorem (since U ∩ V U ∩ V, being convex, is path connected) - user515010 Mar 21, 2021 at 12:51 ( ) is calledprimitiveif there exists a submodule U of V such that x 2=U but n + x ˆU. Thus if n + x = 0, then x is primitive. If M has a primitive vector x whose weight 6= then U(g)x is a proper submodule, so V is not irreducible if such primitive vectors may be found. Theorem If 2h then there is a unique irreducible highest weight Primitive Guoning Wu December 23, 2018 In differential calculus, as we verified on the examples of previous section, in addition to knowing how to differentiate functions and write relations be-. Let R(u,v) be a rational function in u and v, that is a quotient of poly-nomials P(u,v) By Gauss Lemma, the polynomial (kg)(th) = (kt)f is primitive so kt, being a divisor of all coefficients of (kt)f, is a unit in R. Thus both k and t are invertible in R and therefore both g and h are in R[x]. 2. Remark. Proposition 1 is true for any R which is integrally closed, but the proof is a bit more involved. 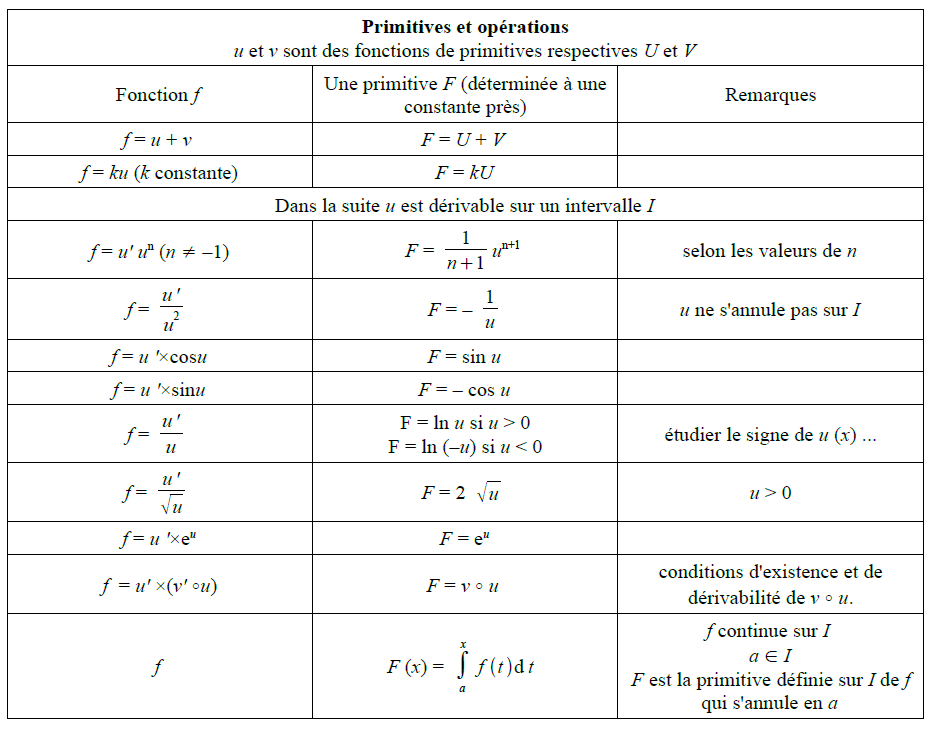
Blatt Multiplikation Ich esse Frühstück calcul des primitives Korrektur Abteilung Arbeiten
Berggrens's tree of primitive Pythagorean triples. In mathematics, a tree of primitive Pythagorean triples is a data tree in which each node branches to three subsequent nodes with the infinite set of all nodes giving all (and only) primitive Pythagorean triples without duplication. A Pythagorean triple is a set of three positive integers a, b. 4.6. THE PRIMITIVE RECURSIVE FUNCTIONS 309 4.6 The Primitive Recursive Functions The class of primitive recursive functions is defined in terms of base functions and closure operations. Definition 4.6.1 Let Σ = {a1,.,a N}. The base functions over Σ are the following functions: (1) The erase function E, defined such that E(w)= , for all w.
5.5: Antiderivatives (Primitives, Integrals) f: E1 → E, we often have to find a function F such that F′ = f on I, or at least on I − Q. We also require F to be relatively continuous and finite on I. This process is called antidifferentiation or integration. Key takeaway #1: u -substitution is really all about reversing the chain rule: . . Key takeaway #2: u -substitution helps us take a messy expression and simplify it by making the "inner" function the variable. Problem set 1 will walk you through all the steps of finding the following integral using u -substitution. 
Tableau des opérations sur les primitives MathBox.Fr
En physique, les intégrales servent également à calculer certaines grandeurs sur des espaces ou des temps donnés. Le travail d'une force d'un point à un autre peut se calculer à l'aide d'une intégrale par exemple. Les primitives sont utilisées quand on a la dérivée d'une fonction et qu'on cherche la fonction elle-même. Primitive Attribute. VOP node. Evaluates an attribute for a given primitive at the specified uv parametric location. Since. 13.0. This operator evaluates an attribute for a given primitive at the specified uv parametric location. If the operation fails, the result is 0. See also. Add Attribute.




