1 minute de lecture 1 commentaire Cet article a pour but de présenter les formules des limites, usuelles comme atypiques. Nous allons essayer d'être exhaustifs pour cette fiche-mémoire Table des matières Les limites issues des puissances Les limites issues de l'exponentielle Les limites issues du logarithme Limites de fonctions usuelles Limite infinie d'une fonction à l'infini lim x = +¥, lim x2 = +¥ et plus généralement, lim xn = +¥, " n ̨n*, lim x fi +¥ x fi +¥ x fi +¥ x fi +¥ +¥ -¥, +¥ si xn n est pair lim x = lim x2 =
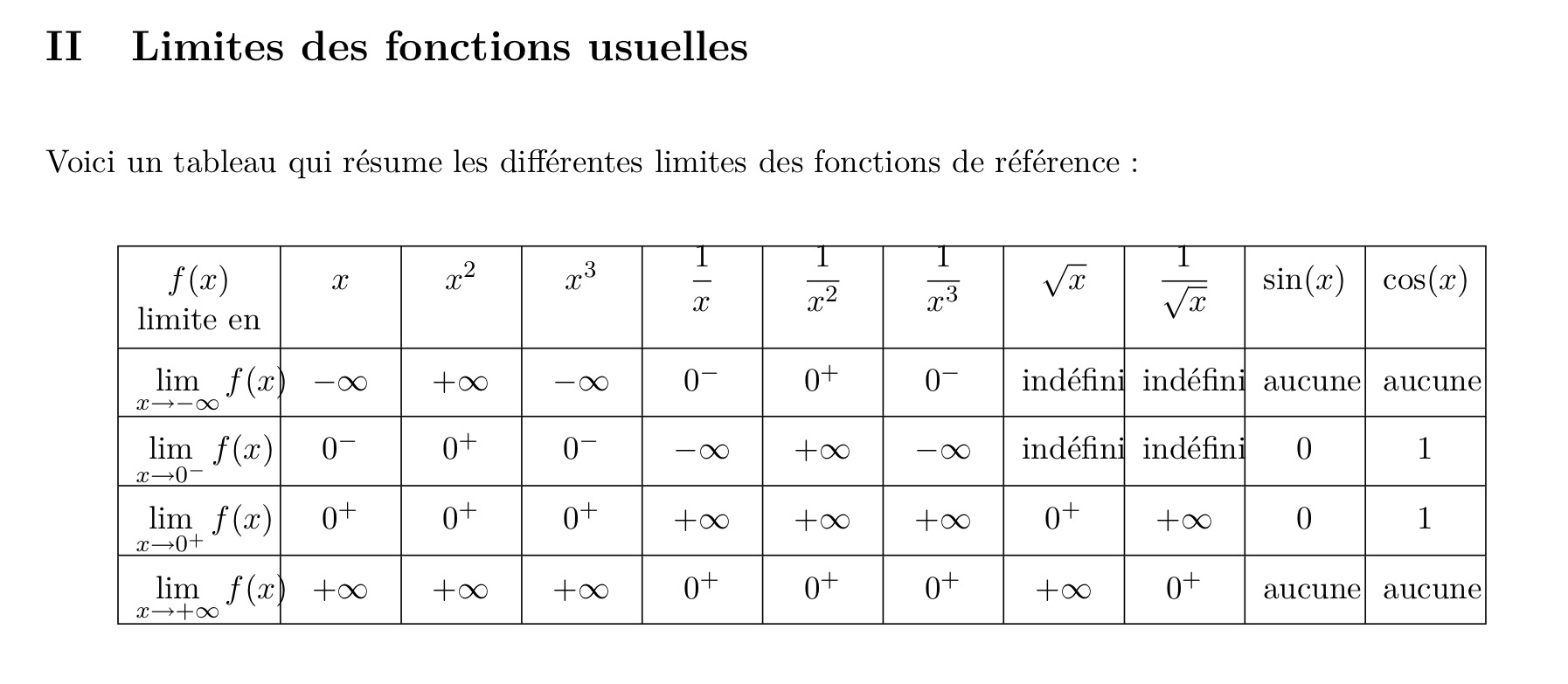
Tableau des limites des fonctions usuelles MathBox.Fr
LIMITES DES FONCTIONS Partie 1 : Limite d'une fonction à l'infini 1) Limite infinie en ∞ Définition : On dit que la fonction admet pour limite +∞ en +∞, si ( ) est aussi grand que l'on veut pourvu que soit suffisamment grand. Remarque : On a une définition analogue en −∞. Exemple : Limites usuelles Limites de fonctions usuelles Puissances de x : pour n >0 n > 0 , Exponentielle : Logarithme : Exponentielle de base a (a x) : Dans ce cas, comme pour la comparaison de fonctions (cf ci-après), le mieux est de repasser à la définition a x =exp (xln (a)), et d'appliquer les théorèmes déjà connus. Fiche technique sur les limites 1 Fonctions élémentaires Les résultats suivants font référence dans de très nombreuses situations. 1.1 Limite en +1 et 1 f (x) xn 1 xn p x 1 p x ln(x) ex lim f (x) x! 1 + 1 + 0 1 + 0 1 + 1 + lim f (x) x!1 n pair 1 + n Voici le tableau des limites de fonctions usuelles indispensables pour la détermination des limites d'autres fonctions en général : 05- Limites de fonctions et asymptotes Limites Laisser un commentaire Votre adresse mail ne sera pas publiée. Autres sujets : Les définitions du produit scalaire Cercle trigonométrique et fonction sinus

Limites de fonctions usuelles formula1 formula 1 en 2020 Graficas matematicas, Funciones
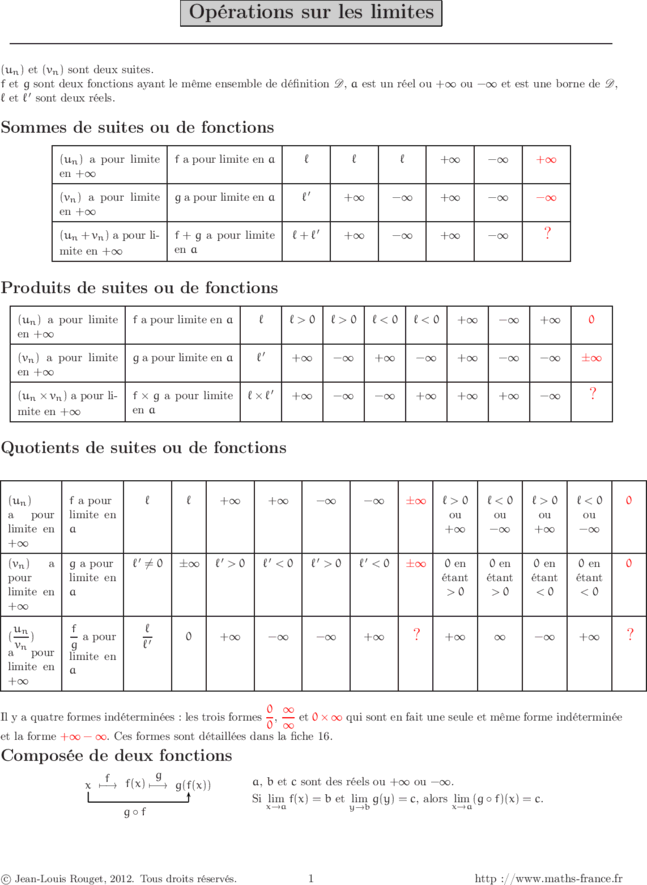
Alors on peut écrire le tableau suivant, selon que la suite converge vers une limite finie ou diverge vers : On a exactement le même tableau pour les cas d'une fonction . Nous ne mentionnerons pas le point , réel ou , en lequel on considère la limite de , que nous noterons donc simplement . La limite de est : Somme 1 1 lim lim = 0 et plus généralement , lim = 0, n = 0 + x + x2 x + xn , lim + 1 lim = 0, lim - = 0 et plus généralement , lim = 0 n * - x2 x - xn Limites de fonctions usuelles en un réel 1 lim = + , n 0+ = + , lim 0+ xn * , lim 0+ = - , lim 0- Limites de la fonction exponentielle : et Limites de la fonction logarithme népérien : et Pour bien comprendre Connaitre la notion de limite d'une fonction. On a abordé dans les fiches précédentes la notion de limite d'une fonction. Dans cette fiche, on va étudier les limites des fonctions usuelles aux bornes de leur ensemble de définition. 1. Objectifs. Déterminer dans des cas simples la limite d'une suite ou d'une fonction en un point, en ± ∞, en utilisant les limites usuelles. Utiliser les croissances comparées et les opérations sur les limites pour déterminer la limite d'une suite ou d'une fonction. Points clés.
LIMITES math (programme mViewer GX Creator Lua Nspire)
On appelle domaine de définition de f l'ensemble noté D f qui représente l'ensemble de x de I tel que f(x) ̨ Y. Limites de fonction 1) Définition • Soit f une fonction de I dans Y et a ̨ I et l ̨ Y. On dit que f admet une limite l quand x tends vers a si : "e > 0, $ a > 0/ " x ̨ I , x - a £ a ⇒ f ( x ) - l £ e On écrira : lim f ( x ) = l fi x a ont des limites nulles en +∞ et −∞ pour les deux premières. Leurs courbes admettent alors l'axe des abscisses comme asymptote horizontale. 1.2 Limite infinie à l'infini Définition 2 : Dire qu'une fonction. On a le tableau de signes de x +2 : x x +2 −∞ −2 +∞.
Posséder un répertoire de limites permettant de déterminer une limite d'une fonction bâtie à partir de fonctions usuelles. Points clés Pour bien comprendre Connaitre les fonctions usuelles. Connaitre la notion de continuité d'une fonction. 1. Fonction carré, fonction cube Les deux fonctions x ↦ x2 et x ↦ x3 sont définies et continues sur . a. Il faut les combiner avec la périodicité et, pour sinus et cosinus, avec les symétries par rapport à l'axe des ordonnées et l'axe des abscisses respectivement. Si sin x = λ ∈ [ −1 ; 1 ], alors ou. = Arcsin λ mod 2π. = π − Arcsin λ mod 2π. Si cos x = λ ∈ [ −1 ; 1 ], alors ou. = Arccos λ mod 2π − Arcsin. = Arctan λ mod.

Mathbox Tableau Des Limites Des Fonctions Usuelles Riset
lorsque n tend vers + ∞ si, pour tout réel A , l'intervalle ] − ∞; A[ contient tous les termes de la suite (un) à partir d'un certain rang. On note lim n → + ∞un = − ∞ La première définition traduit le fait que la suite dépasse n'importe quel seuil donné sans jamais repasser en dessous par la suite. III/ Théorèmes de comparaison : A partir du tableau donnant les limites des suites usuelles, on va pouvoir déterminer d'autres limites par comparaison. Le principe est simple : si par exemple on sait qu'une suite est plus grande qu'une suite tendant vers + ∞ + ∞ on peut en déduire que la première suite tend elle aussi vers + ∞. + ∞.




