A geometriai transzformációkról általában Egybevágósági transzformációk A transzformáció neve Fix pontja(i) Helyettesíthető egyenesre (tengelyre) vonatkozó tükrözás a tengely minden pontja a tengely körüli 180 -os (térbeli) elforgatás pontra vonatkozó tükrözés a tükrözés középpontja a tükrözés középpontján. Köszönöm a Figyelmet Geometriai transzformáció fogalma. Középontos tükrözés Egybevágósági transzformáció NEVEZETES SZÖGPÁROK -Egyállású szögek -Társszögek -Fordított állású szögek mellékszögek,csúcsszögek Egybevágósági (távolságtartó) transzformációknak azokat a geometriai

Egybevágósági transzformációk Párosító
Oktatás: az egybevágósági transzformációk alapfogalmainak megértése, rendszerezése. A transzformáció során megmaradó és változó tulajdonságok felismerése. Bizonyítások menetének gyakorlása. Nevelés: a csoportos munka során a diákok lehetőséget kapnak a közös munkára. Lehetőség szerint Transzformációk tulajdonságai távolságtartó: szakasz és képe ugyanolyan hosszúságú; szögtartó: szög és képe ugyanolyan nagyságú;. Egybevágó síkidomok Két síkidomot egybevágónaknevezünk, ha véges sok egybevágósági transzformáció egymást követő alkalmazásával egymásba vihetők. Az egybevágó alakzatok nem. A távolságtartó geometriai transzformációt egybevágósági transzformációnak nevezzük. Vagyis ez olyan geometriai transzformáció, aminél bármely két pont távolsága megegyezik a nekik megfelelő képpontok távolságával. A legegyszerűbb egybevágósági transzformáció az, ami a sík minden pontjához önmagát rendeli hozzá. Egybevágósági transzformációnak (továbbiakban röviden egybevágóságnak) nevezzük a tér önmagára vonatkozó kölcsönösen egyértelmű leképezését, amely a szakaszokat velük egybevágó szakaszokba viszi.. A tér egybevágóságai a kompozíció műveletével csoportot alkotnak. Ez a csoport nem kommutatív.A műveletet jobbról balra végezzük el, azaz pl ha T egy tengelyes.
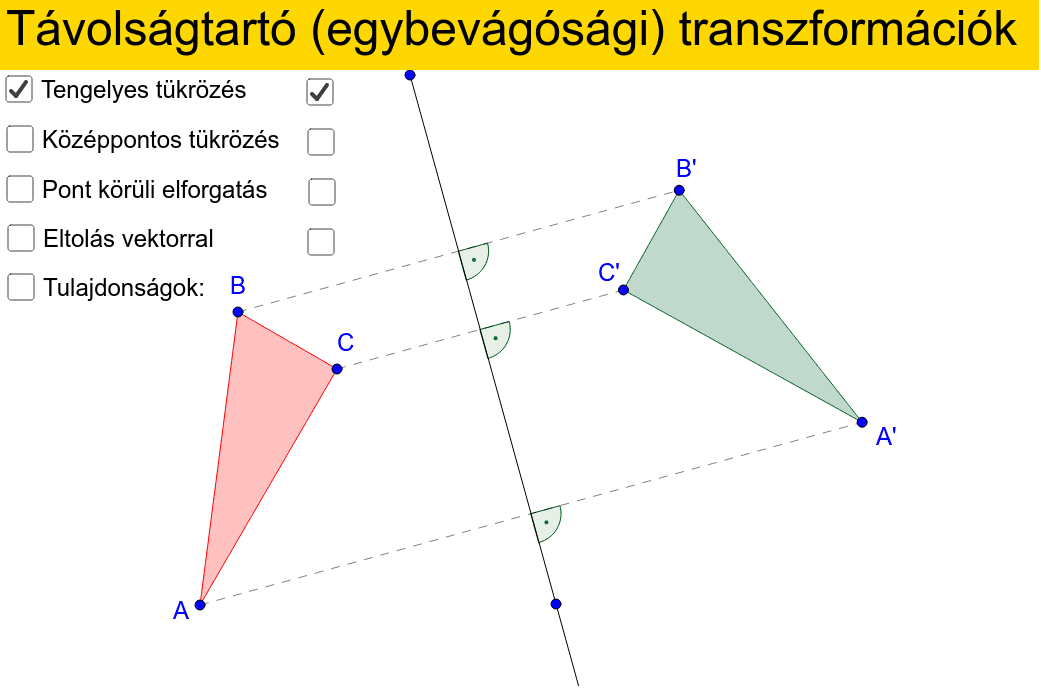
Távolságtartó (egybevágósági transzformációk) GeoGebra
tartozó transzformációk részcsoportot alkotnak az egybevágósági transzformációk csoportjában. Például az eltolások, vagy valamely rögzített geometriai alakzatot önmagába képező egybevágóságok részcsoportot alkotnak az összes egybevágóság alkotta csoportban. • Példák: - Bármely mozgás egybevágóság. Egybevágósági transzformáció fogalma. Definíció: Egybevágósági (távolságtartó) transzformációknak azokat a geometriai transzformációkat nevezzük, amelyeknél bármely két pont távolsága egyenlő a pontok képeinek távolságával. A legnevezetesebb egybevágósági transzformációk: Tengelyes tükrözés; Középpontos. Egybevágósági (távolságtartó) transzformációknak azokat a geometriai transzformációkat nevezzük, amelyeknél bármely két pont távolsága egyenlő a pontok képei. Ezek egybevágósági transzformációk voltak (tengelyes tükrözés, középpontos tükrözés, pont körüli forgatás, eltolás), majd a középpontos hasonlósággal ismerkedtünk meg. Az egybevágósági transzformációk tárgyalását a tapasztalatainkra építettük. Megállapítottuk, hogy bármely szakasz képe ugyanolyan hosszú.

PPT Geometriai Transzformációk PowerPoint Presentation, free download ID491006
De az egybevágósági transzformációk közül mindet, amiről csak álmodhatunk. Hogyha pedig egymással párhuzamos tengelyekre tükrözünk… Akkor a háromszög így szépen arrébb tolódik. Ez egy újabb egybevágósági transzformáció. És úgy hívják, hogy eltolás. Az eltolás iránya merőleges a tengelyekre. Az egybevágósági transzformációk rendszerezése Az eddig részletesen tanult transzformációk: - tengelyes tükrözés - középpontos tükrözés - eltolás A forgatásról szóljunk! Transzformációk egymás utáni alkalmazása A hasonlóság és az affinitás A középpontos hasonlóság - feladattípusok Végezzük el koordináta.
Az egybevágósági transzformáció olyan geometriai transzformáció, amely távolságtartó, azaz bármely P és Q pontok esetén ha a P pont képe P' és Q pont képe Hirdetés. Tételek Irodalom Nyelvtan. (A geometriai transzformációk olyan függvények, amelyeknek értelmezési tartományuk és értékkészletük is ponthalmaz.). Egybevágósági transzformáció: olyan pont-pont függvény, ami valamilyen síkbeli alakzatot meghatározó pontokhoz, vele egybevágó síkidomot meghatározó pontokat rendel. Pl. a fenti négy esetben az A, B, és C pontok egy háromszöget határoznak meg; a tengelyes

PPT Geometriai transzformációk PowerPoint Presentation, free download ID3643449
témakör. share_arrow_outline bell search dot_3_horizontal bell search dot_3_horizontal Az egybevágósági transzformációk leírása az identikus transzformáció, a tengelyes és a középpontos tükrözés leírásával még nem teljes. Az említetteken kívül szót ejtünk még további két egybevágósági transzformációról. Ha ránézel a tanteremben az órára, akkor azt láthatod, ahogy az idő múlásával a.



