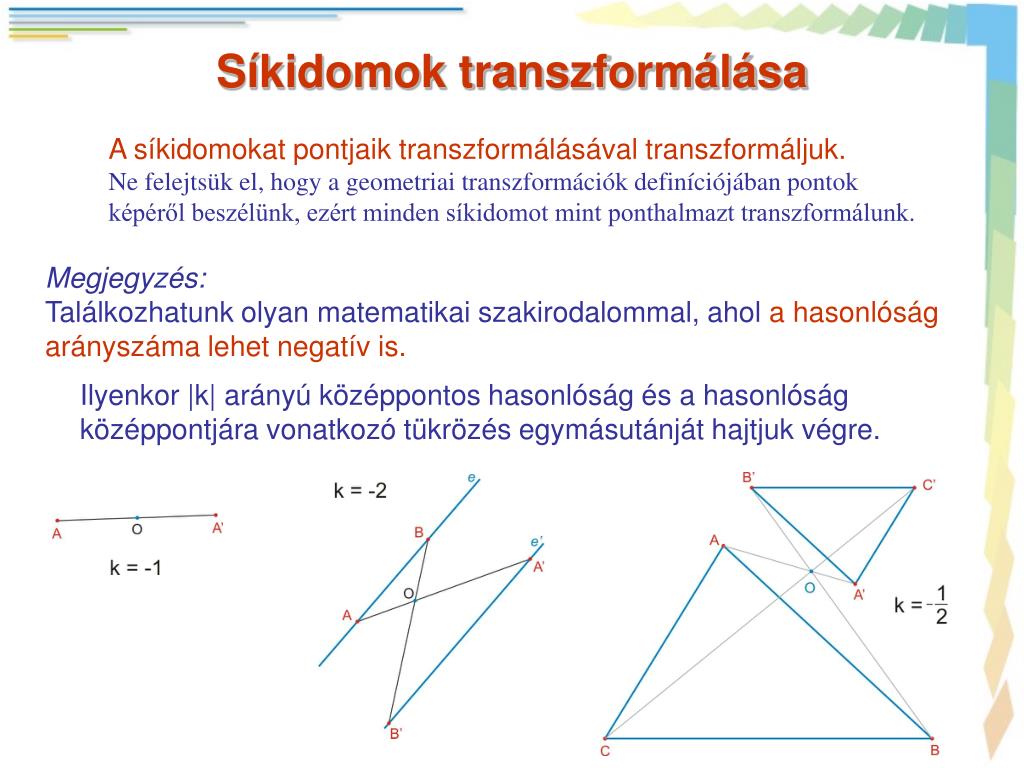
- A középpontos hasonlósági transzformáció szögtartó - Ha az arány λ, akkor bármely AB szakasz képe az eredeti AB szakasz hosszának λ-szorosa. - Ha λ =1, akkor a transzformáció egybevágóság, ha λ = -1, akkor középpontos tükrözés. - A transzformáció irányítástartó. A középpontos hasonlóság tulajdonságai: 1. Egyetlen fix pont van, a hasonlóság (O) középpontja. 2. Szögtartó, azaz szög képe vele azonos nagyságú szög. 3. A középpontos hasonlóság aránytartó, azaz bármely szakasz képének és az eredeti szakasznak az aránya egyenlő, megegyezik a hasonlóság arányával. 4. Körüljárástartó. 5. Egyenes képe egyenes. 6.

Középpontos hasonlóság GeoGebra
Definíció: Hasonlósági transzformációnak olyan geometriai transzformációt nevezünk, amely középpontos hasonlóság és távolságtartó (egybevágósági) transzformáció egymás utáni elvégzésével (szorzatával) jön létre. A λ (λ≠0) számot a középpontos hasonlóság arányának nevezzük. Ha λ = 1, akkor a középpontos hasonlóság identitás. Ha λ = -1, akkor a középpontos hasonlóság középpontos tükrözés. Tehát a középpontos hasonlóság esetben egybevágósági transzformációvá válik. Középpontos hasonlóság. A középpontos hasonlóság egy középponttal és egy arányszámmal megadható hasonlósági transzformáció. Az arányszám nem nulla, és lambdával jelölik. A középpontos hasonlóság a távolságokat |λ|-szeresükre növeli. Tudásbázis Matematika Matematika. Matematika - 10. osztály. Geometria. Geometriai transzformációk. A középpontos hasonlósági transzformáció tulajdonságai. A párhuzamos szelő szakaszok tétele. A középpontos hasonlósági transzformáció tulajdonságai. A párhuzamos szelők tétele. A párhuzamos szelők tételének megfordítása.
PPT Hasonlóság modul PowerPoint Presentation, free download ID6032634
Ezt a geometriai transzformációt középpontos hasonlósági transzformációnak nevezzük. Meg kell adnunk egy O pontot, a hasonlóság középpontját, és egy $\lambda $, nem nulla valós számot, a hasonlóság arányát. A középpontos hasonlósági transzformáció az O ponthoz önmagát rendeli. Minden más P ponthoz az OP egyenes azon P' pontját, amelyre\ [OP' = \left| \lambda \right| \cdot OP\], valamint ha \ [\lambda \] pozitív, akkor P' az OP félegyenesen, ha negatív, a P-vel ellentétes félegyenesen van. Majd az A'B'C'Δ-t egy O 2 középpontú középpontos hasonlóság kicsinyíti az A"B"C"Δ- be. Definíció: Két alakzatot hasonlónak nevezünk, ha van olyan hasonlósági transzformáció, amellyel az egyik alakzatot a másikba vihetjük át. A hasonlóság jele: ∼. Két háromszög hasonló, ha: 1. Az egybevágósági és a középpontos hasonlósági transzformáció definícióiból és tulajdonságaiból beláthatók a hasonlósági transzformációk tulajdonságai is. 1. Egyenes képe egyenes. 2. A hasonlósági transzformáció szögtartó. 3. A arányú hasonlósági transzformáció bármely szakasz hosszát hosszúságúra.

PPT Hasonlóság modul PowerPoint Presentation, free download ID6032634
A középpontos hasonlósági transzformációhoz adott egy O O pont, ez a középpont, és egy λ λ nem nulla valós szám, ez a hasonlóság aránya. A tér minden P P pontjához egy P′ P ′ pontot rendel a következőképp: 1. ha P = O P = O, akkor P′ = P P ′ = P. A középpontos hasonlósági transzformáció hozzárendelési szabálya: Adott egy O pont (a középpontos hasonlósági transzformáció középpontja) és egy , nullától különböző, szám. A középpont képe fixpont. Ha egy P pont nem illeszkedik a középpontra, akkor a P pont képe az O pontból kiinduló vektor P' végpontja.
Transzformáció (matematika) A „Transzformáció" szócikk ide irányít át. Hasonló címmel lásd még: Transzformáció (egyértelműsítő lap). A geometriai transzformáció geometriai objektumok között létesitett megfeleltetés, reláció . Szűkebb értelemben egy-egyértelmű : P→P* (pont-pont) megfeleltetés. A középpontos hasonlósági transzformáció Az előző tanévben részletesen foglalkoztunk a síkbeli egybevágósági transzformációkkal. Megadtuk a transzformációk hozzárendelési utasítását,.

Hasonlósági transzformáció fogalma YouTube
55. Szerkesztések középpontos hasonlóság alkalmazásával 56. Gyakorlás 57. A hasonlósági transzformáció fogalma A hasonlósági transzformáció fogalma, a transzformáció aránya 58. A hasonlósági transzformáció fogalma Alakzatok hasonlósága, háromszögek hasonlósági kritériumai 59. Gyakorlás 60. Középpontos hasonlósági transzformáció Szerző: Nyögéri Imre Témák: Geometria A csúszkán változtatható a középpontos hasonlóság aránya és megfigyelhető az ABC háromszög középpontos hasonlósággal kapott képe. Új anyagok Dinamikus koordináták A légy-piszok E 02 Az Elliptikus sík félgömb-modellje E 04 Legyen adott az E-síkon. Magasságpont (ok)




