A geometriában egy sokszög köréírt köre (esetleg: körülírt vagy körülírható (stb.) köre) az a kör, ami a poligon összes csúcsán átmegy. Az ilyen sokszög neve húrsokszög. Minden háromszögnek van körülírható köre (húrháromszög), [1] háromnál több csúcsú poligonokra ez általában nem igaz. Példa a háromszög köré írható körével kapcsolatban 1. Feladat: Egy háromszög egyik oldala 6 cm-es, a köré írt kör sugara 4 cm-es. Milyen messze van a köréírt kör középpontja az adott oldaltól? Megoldás: Készítsünk egy vázlatot! Tudjuk, hogy a köréírt kör középpontja az oldalfelező merőlegesek metszéspontja.

HÁROMSZÖG KÖRÉ ÍRHATÓ KÖRE YouTube
A hozzáírt kör a háromszög egyik oldalát és a másik két oldalának meghosszabbítását érintő kör. Minden háromszögnek három hozzáírt köre van. A hozzáírt körök középpontjai megkaphatók a háromszög egy belső és a háromszög két másik szögéhez tartozó külső szögfelező metszéspontjaként. Köré írható kör sugara: Az ötágú csillag ( pentagramma) a szabályos ötszög átlóiból szerkeszthető. Schläfli-szimbóluma . A pentagramma és az ötszög oldalának aránya az aranymetszésnek felel meg. Az ötágú csillag belső csúcspontjait összekötve egy kisebb szabályos ötszöget kapunk. Szerkesztés 0:00 / 3:12 Háromszög köré írható köre 1. LZmatek 1.36K subscribers 18K views 2 years ago A tanítás támogatása Iratkozz fel: @LZmatek Hegyesszögű háromszög köré írható köre középpontjának és a. Eredmények: A c oldal A terület: a*ma/2 Derékszögű háromszög szögfüggvények: Sin Cos Tan Derékszögű háromszög szögfüggvények: Szinusz: sin: a szöggel szemközti befogó / átfogó Koszinusz: cos: a szög melletti befogó / átfogó Tangens: tan: a szöggel szemközti befogó / a szög melleti befogó A tompaszögű háromszög területe és kalkulátor:

Háromszög köré írható kör YouTube
A geometriában egy háromszög köréírt kör, az a kör, ami a háromszög összes csúcsán átmegy.http://videotanar.hu/ Hatszög A geometriában hatszög (hexagon) az olyan sokszög, amelynek hat oldala és hat csúcsa van. Minden hatszögre igaz, hogy szögeinek összege 720°. Szabályos hatszög Szabályos hatszög A szabályos sokszögek szögeire ismert az alábbi képlet : amely n=6 esetben Területe Témák: Kör, Geometria, Háromszögek Bármely háromszög oldal felező merőlegesei egy pontban metszik egymást. Ez a pont a háromszög köré írható kör középpontja. Hol található a köré írt kör középpontja, ha a háromszög: a) hegyesszögű b) derékszögű c) tompaszögű Új anyagok Bicentrikus négyszögek 10_02 Leképezés domború gömbtükörrel A háromszög köré írt köre az a kör, amely átmegy a háromszög mindhárom csúcsán. Ezt a kört úgy kapjuk meg, hogy megkeressük a háromszög oldalfelező merőlegeseit, és ezek metszéspontja adja a köré írt kör középpontját. Ezután kapjuk meg a kör sugarát: a középpont és bármelyik csúcs távolsága lesz a köré.

Háromszög Köré Írható Kör Középpontja A Háromszög Zanza.Tv
Ebben a videóban feladatokat oldunk a szabályos háromszög (egyenlő oldalú háromszög) beírt illetve köréírt körével kapcsolatba. A teljes sorozat (kör és anna. Iratkozz fel: @LZmatek Húrtrapéz köré írható körének szerkesztése belső kör középpont, külső kör középpont és a trapéz körvonalán lévő kör középpont esetén._.
A beírt kör középpontja a háromszög szögfelező egyeneseinek a metszéspontja. A beírt kör a háromszög minden oldalát egy-egy pontban érinti. Példa a háromszögbe írható körről. Feladat: Szerkesszük meg az ABC háromszög beírt körét, ha a = 6 cm b = 9 cm és az a és b oldalak bezárt szöge 𝛾 = 60°. Mind az 1300 db, ingyenes és reklámmentes videó megtalálható itt: http://www.zsenileszek.hu/Ha hibáztunk a videóban, írj kommentet, ha tetszett, akkor iratko.
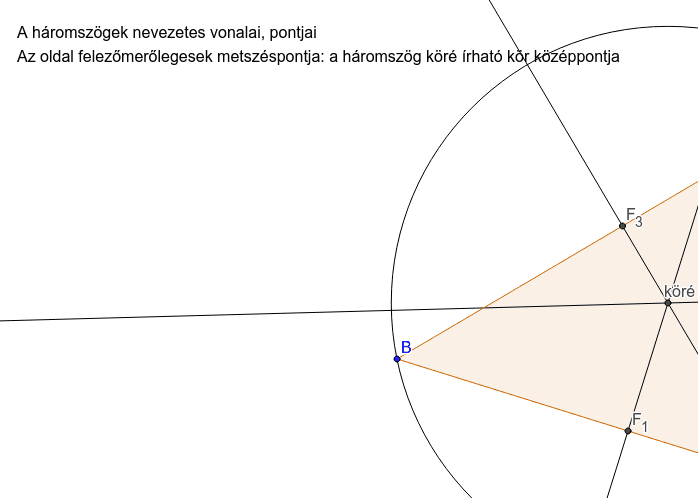
A háromszög köré írható kör GeoGebra
A háromszög köré írható kör. A képen egy háromszög köré írható kört látsz. Ha a képre kattintasz lenyomott egérrel a háromszög csúcsait bármerre tudod mozgatni. Így meg tudod nézni, hogy a háromszög köré írható kör középpontja hová esik hegyesszögű, derékszögű illetőleg tompaszögű háromszög esetén. A háromszög köré írható kör középpontjának és sugarának meghatározása számítással - kicsit másként Egy érdekes és egyszerűnek mondható megoldásra bukkantunk az [ 1 ] műben, ahol igazából csak a Pitagorász - tételt alkalmazták, meg némi algebrát. Minthogy ez a könyvecske nem sűrűn kerül - csak úgy - az Olvasó kezébe, ezért készült belőle ez az írás.




