Parametric Equation of an Ellipse An ellipse can be defined as the locus of all points that satisfy the equations x = a cos t y = b sin t where: x,y are the coordinates of any point on the ellipse, a, b are the radius on the x and y axes respectively, ( * See radii notes below ) t is the parameter, which ranges from 0 to 2π radians. Options Hide The parametric equations limit \(x\) to values in \((0,1]\), thus to produce the same graph we should limit the domain of \(y=1-x\) to the same.. This final equation should look familiar -- it is the equation of an ellipse! Figure 9.26 plots the parametric equations, demonstrating that the graph is indeed of an ellipse with a horizontal.
Parametric equation Q No 1 Equation of Ellipse YouTube
The parametric equation of an ellipse is x = a cos t y = b sin t It can be viewed as x coordinate from circle with radius a, y coordinate from circle with radius b. When given an equation for an ellipse centered at the origin in standard form, we can identify its vertices, co-vertices, foci, and the lengths and positions of the major and minor axes in order to graph the ellipse. See Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\). The collection of points that we get by letting t t be all possible values is the graph of the parametric equations and is called the parametric curve. To help visualize just what a parametric curve is pretend that we have a big tank of water that is in constant motion and we drop a ping pong ball into the tank. Parametric form. In parametric form, the equation of an ellipse with center (h, k), major axis of length 2a, and minor axis of length 2b, where a > b and θ is an angle in standard position can be written using one of the following sets of parametric equations. when the major axis is horizontal. x = h + a·cos(θ), y = k + b·sin(θ)
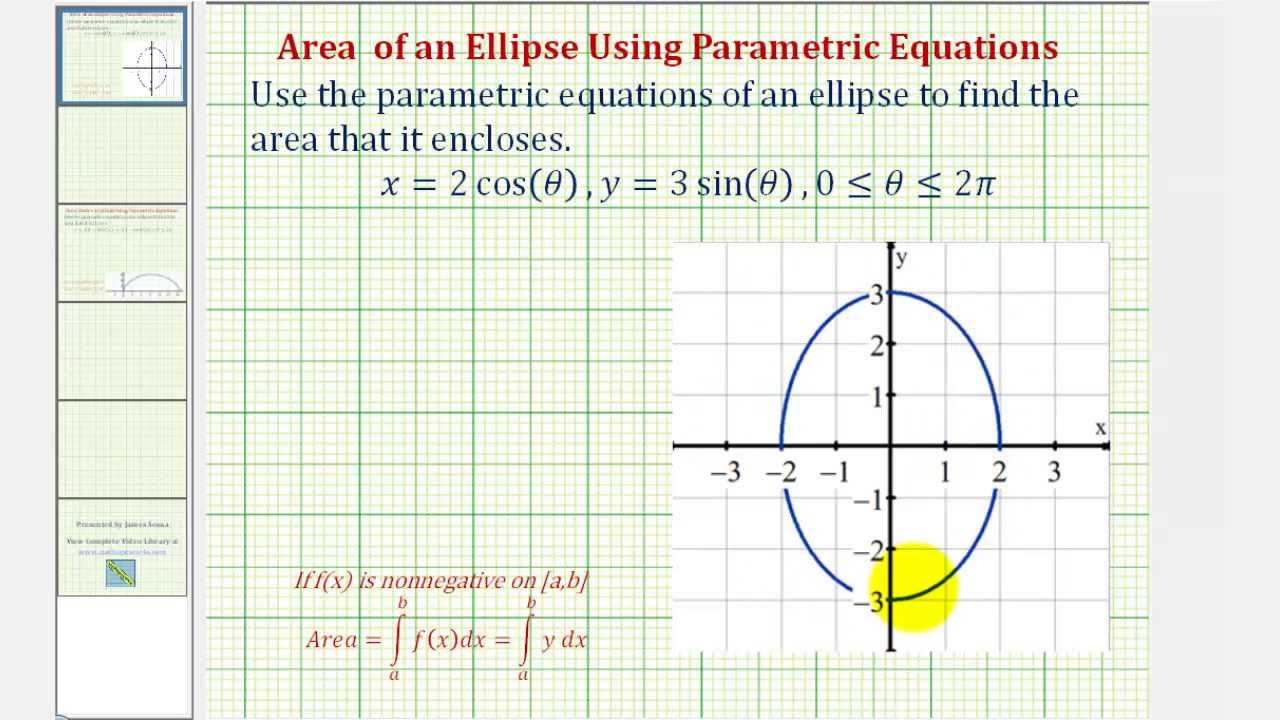
Integration Application Area Using Parametric Equations Ellipse YouTube
The parametric equation of an ellipse centered at \((0,0)\) is \[f(t) = a\cos t, \quad g(t) = b\sin t.\] Our approach is to only consider the upper half, then multiply it by two to get the area of the entire ellipse. First, we need to find the left and right bounds in terms of \(t\), such that In the two-dimensional coordinate system, parametric equations are useful for describing curves that are not necessarily functions. The parameter is an independent variable that both x and y depend on, and as the parameter increases, the values of x and y trace out a path along a plane curve. The parametric equation of an ellipse is: x = a cos t y = b sin t Understanding the equations We know that the equations for a point on the unit circle is: x = cos t y = sin t Multiplying the x formula by a scales the shape in the x direction, so that is the required width (crossing the x axis at x = a ). Since the parametric equation is only defined for \(t > 0\), this Cartesian equation is equivalent to the parametric equation on the corresponding domain.. This is a Cartesian equation for the ellipse we graphed earlier. Parameterizing Curves. While converting from parametric form to Cartesian can be useful, it is often more useful to.

How to Write the Parametric Equations of an Ellipse in Rectangular Form YouTube
1.3.1 Ellipse Parametric Equation. x ( t) = r cos ( θ) + h y ( t) = r sin ( θ) + k. The conic section most closely related to the circle is the ellipse. We have been reminded in class that the general equation of an ellipse is given by. x 2 a 2 + y 2 b 2 = 1. (1) where is the semimajor axis and the origin of the coordinate system is at one of the foci. The corresponding parameter is known as the semiminor axis . The ellipse is a conic section and a Lissajous curve . An ellipse can be specified in the Wolfram Language using Circle [ x, y, a , b ].
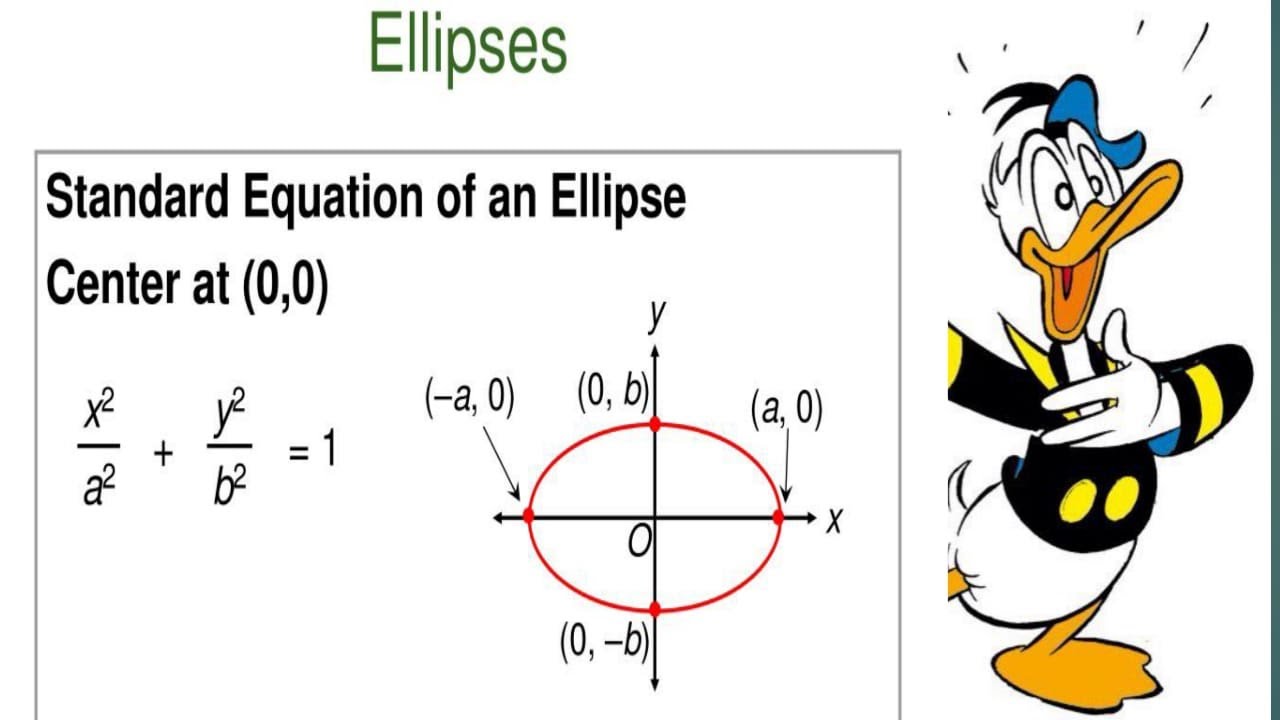
The standard parametric equation is: Ellipses are the closed type of conic section: a plane curve tracing the intersection of a cone with a plane (see figure). Ellipses have many similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. An ellipse is the locus of a point whose sum of the distances from two fixed points is a constant value. The two fixed points are called the foci of the ellipse, and the equation of the ellipse is x2 a2 + y2 b2 = 1 x 2 a 2 + y 2 b 2 = 1. Here. a is called the semi-major axis.

Parametric Equations of Ellipse Example 1 椭圆参数方程 YouTube
Formula to determine the perimeter of an ellipse is P = 2π a2+b2 2− −−−√ P = 2 π a 2 + b 2 2 or P = π 2(a2 +b2)− −−−−−−−√ P = π 2 ( a 2 + b 2) where a is the length of the semi-major axis and b is the length of the semi-minor axis. Area of Ellipse: The area of an ellipse is the measure of the region present inside it. Now from P draw PM perpendicular to the major axis of the ellipse and produced MP cuts the auxiliary circle x2 2 + y2 2 = a2 2 at Q. Join the point C and Q. Again, let ∠XCQ = ф. The angle ∠XCQ = ф is called the eccentric angle of the point P on the ellipse. The major axis of the ellipse x2 a2 x 2 a 2 + y2 b2 y 2 b 2 = 1 is AA' and its.




