Aturan Cosinus. Aturan Cosinus - Merupakan aturan dalam pelajaran trigonometri yang menggabungkan fungsi kosinus dengan sisi - sisi segitiga. Secara umum, pembahasan ini disediakan selama sekolah menengah dan termasuk dalam bab Trigonometri. Rumus aturan ini terdiri dari tiga persamaan. Sesuai dengan jumlah sudut dan jumlah sisi segitiga. Aturan Cosinus merupakan aturan yang menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga. Aturan cosinus dapat digunakan untuk menentukan unsur-unsur lain dalam suatu segitiga sembarang untuk dua kasus yaitu saat tiga sisi ketahui dan saat dua sisi dan sudut apitnya diketahui. Seperti yang.

Aturan Cosinus Cara menentukan panjang sisi dan besar sudut
A. Aturan Cosinus dan Pembuktian. Pada segitiga ABC dengan panjang sisi BC = a, panjang sisi AC = b, dan panjang sisi AB = c, maka berlaku: a 2 = b 2 + c 2 − 2 b c. cos A. b 2 = a 2 + c 2 − 2 a c. cos B. c 2 = a 2 + b 2 − 2 a b. cos C. Pembuktian Aturan Cosinus: (1) Pembuktian: a 2 = b 2 + c 2 − 2 b c cos A. Perhatikan gambar berikut ini! Di sini, kamu akan belajar tentang Aturan Cosinus melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal. Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Aturan Cosinus. Kita ambil contoh, apabila sisi siku-siku dari segitiga siku-siku dibuat lebih dekat (sudut yang diapitnya semakin kecil) maka sudut siku-sikunya tersebut akan menjadi sudut lancip, dan diperoleh rumus c 2 < a 2 + b 2.Kemudian untuk membuat pertidaksamaan ini menjadi suatu persamaan, maka kita perlu mengurangi a 2 + b 2 dengan nilai tertentu. Law of cosines. Fig. 1 - A triangle. The angles α (or A ), β (or B ), and γ (or C) are respectively opposite the sides a, b, and c. In trigonometry, the law of cosines (also known as the cosine formula or cosine rule) relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite.

Konsep Dasar Aturan Cosinus Matematika Wajib Kelas 10 Contoh Soal
Aturan Cosinus. Dalam Modul Matematika Umum Kelas X yang disusun oleh Tinasari Pristiyanti (2020), aturan cosinus adalah aturan yang menghubungkan antara nilai cosinus dan kuadrat panjang sisi pada salah satu sudut segitiga.. Dengan kata lain, aturan cosinus berfungsi sebagai perbandingan panjang dalam suatu segitiga antara sisi samping sudut dengan sisi miringnya. Rumus tersebut dapat diubah menjadi aturan kosinus dengan mensubtitusi CH = (CB) cos (π − γ) = − (CB) cos γ . Perkembangan trigonometri di zaman keemasan Islam memperluas cakupan dan memperbaiki bentuk dari teorema oleh Euklides tersebut. Pada abad kesepuluh, Al-Battani memperumum hasil perolehan Euklid untuk geometri bola. Aturan Cosinus. Pada segitiga ABC berlaku aturan cosinus sebagai berikut. a 2 =b 2 +c 2 -2bccosA. b 2 =a 2 +c 2 -2accosB. c 2 =a 2 +b 2 -2abcosC. Jika dalam segitiga ABC diketahui sisi-sisi a, b, dan c (sisi-sisi-sisi) maka besar sudut-sudut A, B, dan C dapat ditentukan dengan rumus: Contoh Soal. Aturan Cosinus adalah rumus trigonometri yang bisa dipakai pada segitiga sembarang. Disebut aturan Cosinus karena menggunakan fungsi Cosinus. Pada segitiga ABC, rumus aturan cosinus adalah sebagai berikut. a 2 = b 2 + c 2 — 2 bc cos A. b 2 = a 2 + c 2 — 2ac cos B. c 2 = a 2 + b 2 — 2ab cos C. Agar lebih mudah dipahami perhatikan contoh.
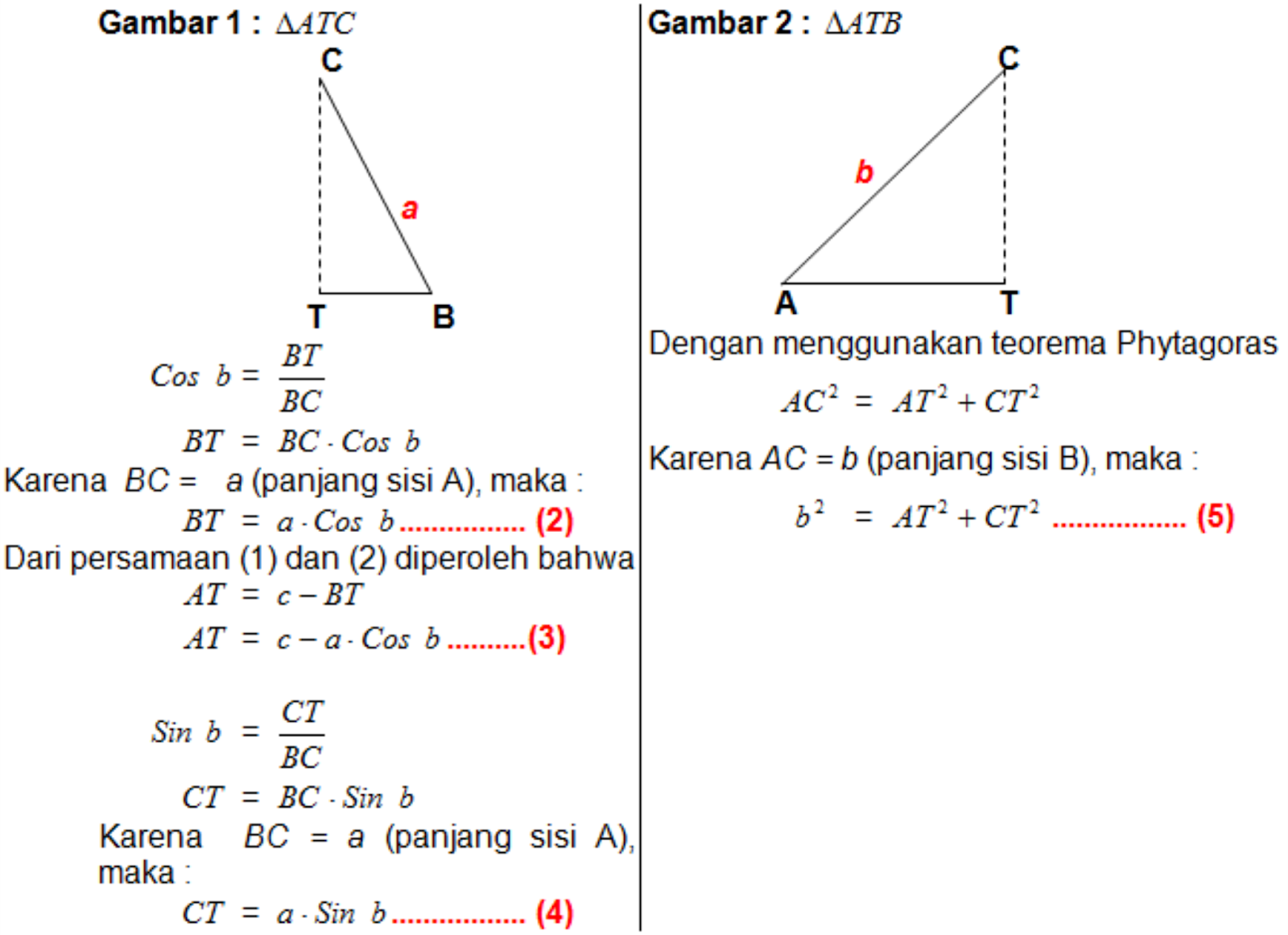
Pembuktian Aturan Cosinus
https://youtu.be/gHAMibCCa58Pembasan aturan cosinus dengan mudah gampang dipahami bersama BOM Matematika#aturancos E. 15 o. Pembahasan: Dari soal diberikan informasi bahwa a 2 - b 2 = c 2 - bc, sehingga dapat diperoleh a 2 = b 2 + c 2 - bc. Rumus cosinus: a 2 = b 2 + c 2 - 2bc ⋅ cos A. Berdasarkan dua persamaan di atas, akan diperoleh nilai cos A. Jadi, besar sudut A adalah 60 o. Jawaban: B.
Contoh Soal Aturan Sinus. 1. Andi sedang mengukur mainan segitiganya yang tiap sudutnya dikodekan dengan A, B, dan C, kemudian diketahui segitiga tersebut memiliki sudut A = 30º, sisi a = 6cm dan sisi b = 8cm. Hitung besar sudut B! Pembahasan. Akan dicari besar sudut B. sin B = (b sin A) / a. sin B = 8 / 6 sin 30̊. sin B = 2 / 3. Aturan Cosinus. Aturan cosinus dapat digunakan untuk menyelesaikan segitiga sembarang di mana dua sisi dan satu sudut pada segitiga diketahui atau saat tiga sisi segitiga diketahui.. Baca juga: Pakai Cuka Apel untuk Redakan Infeksi Sinus Secara umum, aturan cosinus menyatakan kuadrat sebuah sisi sama dengan jumlah kuadrat dari kedua sisi lainnya, dikurangi dua kali hasil kali kedua sisi.

ATURAN COSINUS YouTube
Aturan Cosinus Author - Muji Suwarno. Date - 23.50 Trigonometri. Dalam pembahasan sebelumnya, telah diuraikan aturan perbandingan trigonometri untuk sudut-sudut pada segitiga siku-siku. Selanjutnya akan dibahas pula aturan perbandingan trigonometri untuk sudut pada segitiga bukan siku-siku. Aturan ini terdiri dari aturan sinus dan aturan kosinus. Contoh 2 - Cara Penggunaan Rumus Aturan Cosinus. Dua kapal A dan B meninggalkan pelabuhan P bersama-sama. Kapal A berlayar dengan arah 30 o dan kecepatan 30 km/jam, sedangkan kapal B berlayar dengan arah 90 o dan kecepatan 45 km/jam. Jika kedua kapal berlayar selama 2 jam, maka jarak kedua kapal tersebut adalah..




