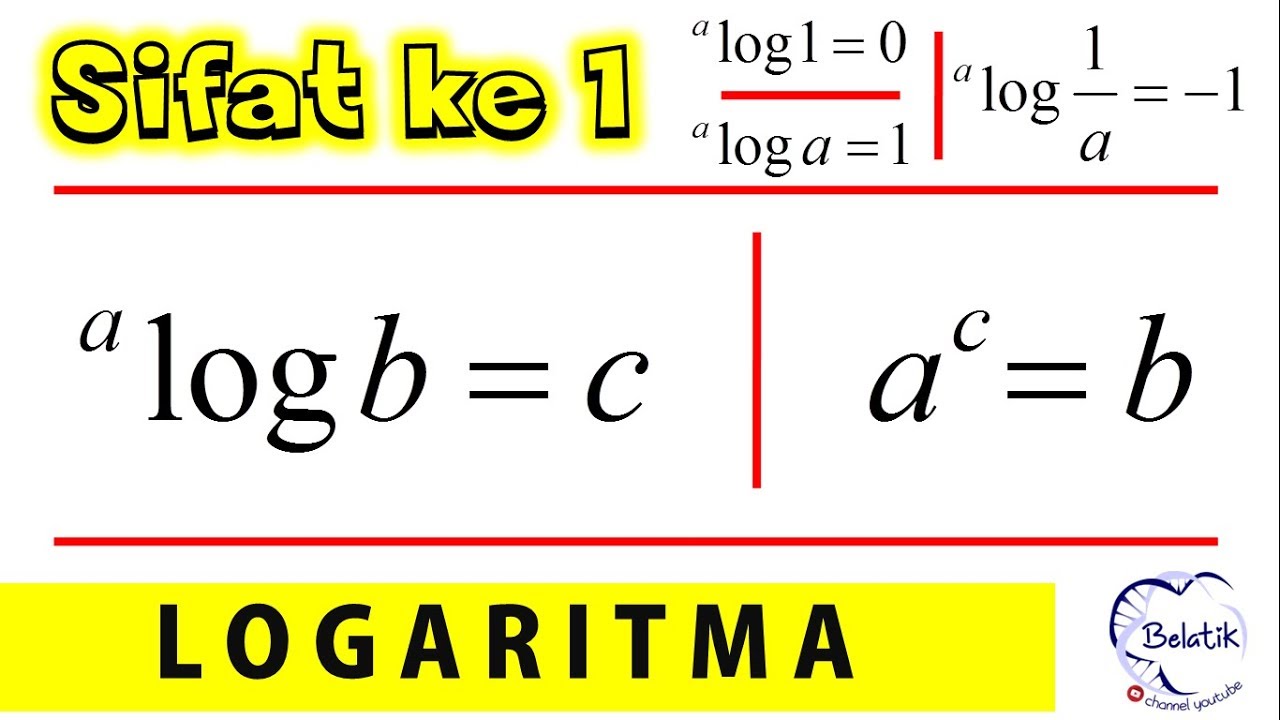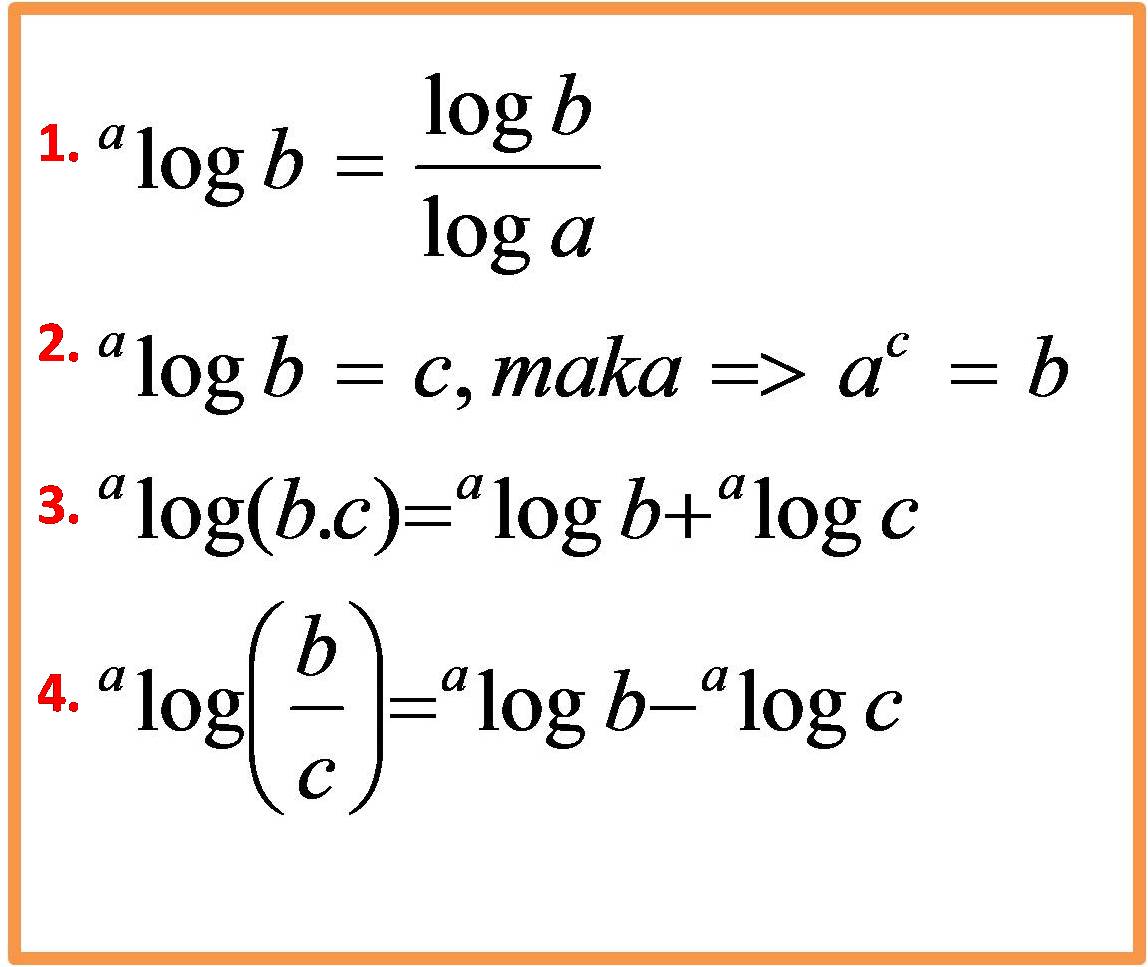Logaritma adalah suatu invers atau kebalikan dari pemangkatan (eksponen) yang digunakan untuk menentukan besar pangkat dari suatu bilangan pokok. Jadi intinya, dengan mempelajari logaritma, kita bisa mencari besar pangkat dari suatu bilangan yang diketahui hasil pangkatnya. "Loh, bukannya mencari besar pangkat itu mudah, ya? Pada penulisan logaritma a log b = c, a disebut bilangan pokok dan b disebut bilangan numerus atau bilangan yang dicari nilai logaritmanya (b > 0) dan c merupakan hasil logaritma.
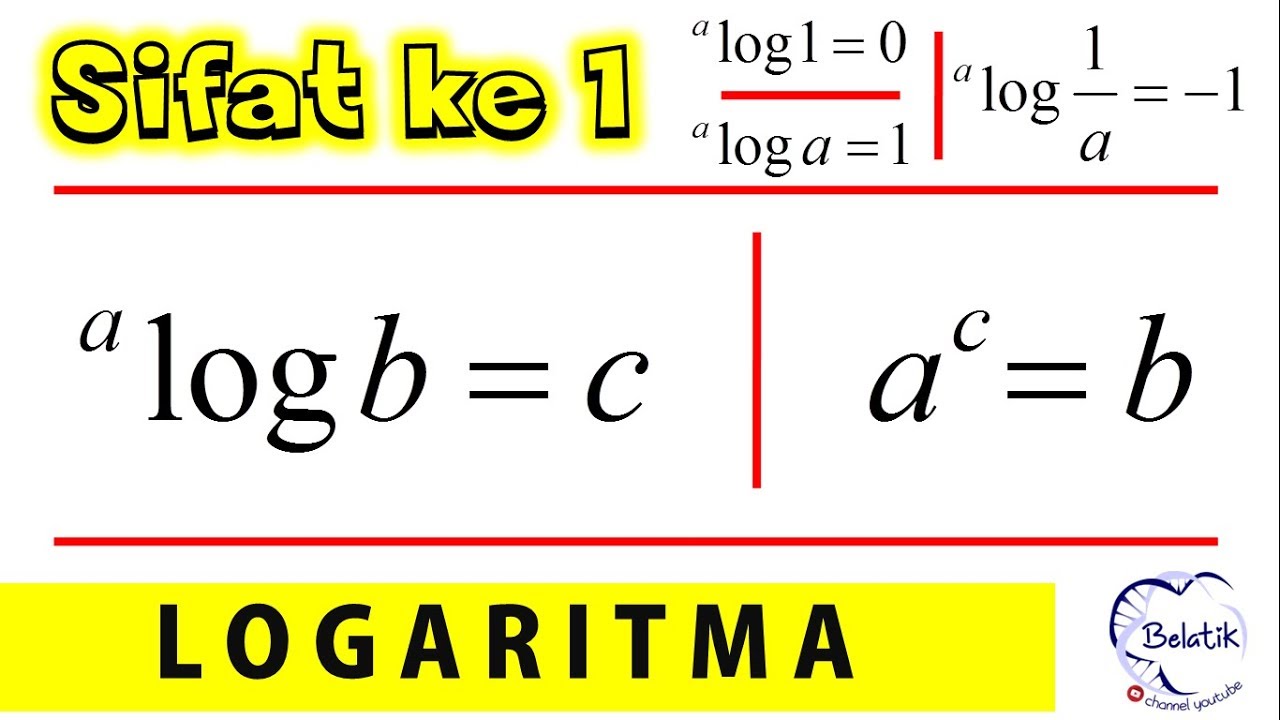
Penjelasan Detail Logaritma Sifat Ke 1 ( a pangkat c = b sama dengan a
Matematika Materi Logaritma: Definisi, Rumus, Sifat, dan Contoh Soalnya Pijar Belajar | 2 July 2023 | 13 Minute Read | Review ★ 5.0 Isi Artikel Pengertian Logaritma Bentuk Umum Logaritma Sifat Sifat Logaritma Persamaan Logaritma 1. Sifat Pertama 2. Sifat Kedua 3. Sifat Ketiga 4. Sifat Keempat 5. Sifat Kelima 6. Sifat Keenam Pertidaksamaan Logaritma Ada tiga bilangan pokok logaritma yang umum beserta kegunaannya. Logaritma dengan bilangan pokok 10 ( b = 10) disebut sebagai logaritma umum, yang biasanya dipakai dalam ilmu sains dan rekayasa. Definisi logaritma Ketika b dipangkatkan dari y sama dengan x: b y = x Maka logaritma basis b dari x sama dengan y: log b ( x ) = y Misalnya ketika: 2 4 = 16 Kemudian log 2 (16) = 4 Logaritma sebagai fungsi kebalikan dari fungsi eksponensial Fungsi logaritmik, y = log b ( x ) adalah fungsi kebalikan dari fungsi eksponensial, x = b y Sumber Khan Academy, Encyclopedia Britannica Cari soal sekolah lainnya KOMPAS.com - Dalam operasi matematika, ada yang dinamakan dengan logaritma. Apakah itu logaritma dan bagaimana sifat-sifat operasinya? Untuk mengetahui jawabannya, simaklah penjelasan di bawah ini! Pengertian logaritma

Sifat Logaritma MacamMacam, Pembuktian, Contoh Soal dan Pembahasannya
dengan a > 0 dan a ≠ 1. Keterangan: a = basis logaritma ac=b atau a log b=c di mana a>0 dan a ≠ 1. Keterangan: a = basis logaritma; 0 < a < 1, atau a > 1. b = bilangan numerus, atau bilangan yang nilai logaritmanya dicari c = besar pangkat (nilai logaritma); c > 0. Misalnya untuk contoh 2 log 8 = c. artinya, c = 3, karena 2 3 = 8. Bagaimana, Detikers? Logaritma Logaritma merupakan kebalikan dari bentuk perpangkatan atau yang umum dikenal sebagai eksponen. Bentuk umum logaritma bisa dinyatakan sebagai berikut. a b = c ⇔ a log c = b Dengan: a = basis b = hasil logaritma; dan c = numerus Ternyata, ada beberapa permasalahan yang bisa diselesaikan menggunakan logaritma lho. Di sini, kamu akan belajar tentang Logaritma melalui video yang dibawakan oleh Bapak Anton Wardaya. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal. Selain itu, kamu juga akan mendapatkan latihan soal interaktif dalam 3 tingkat kesulitan (mudah, sedang, sukar). Oleh karenanya, pembahasan ini bisa langsung kamu praktikkan.
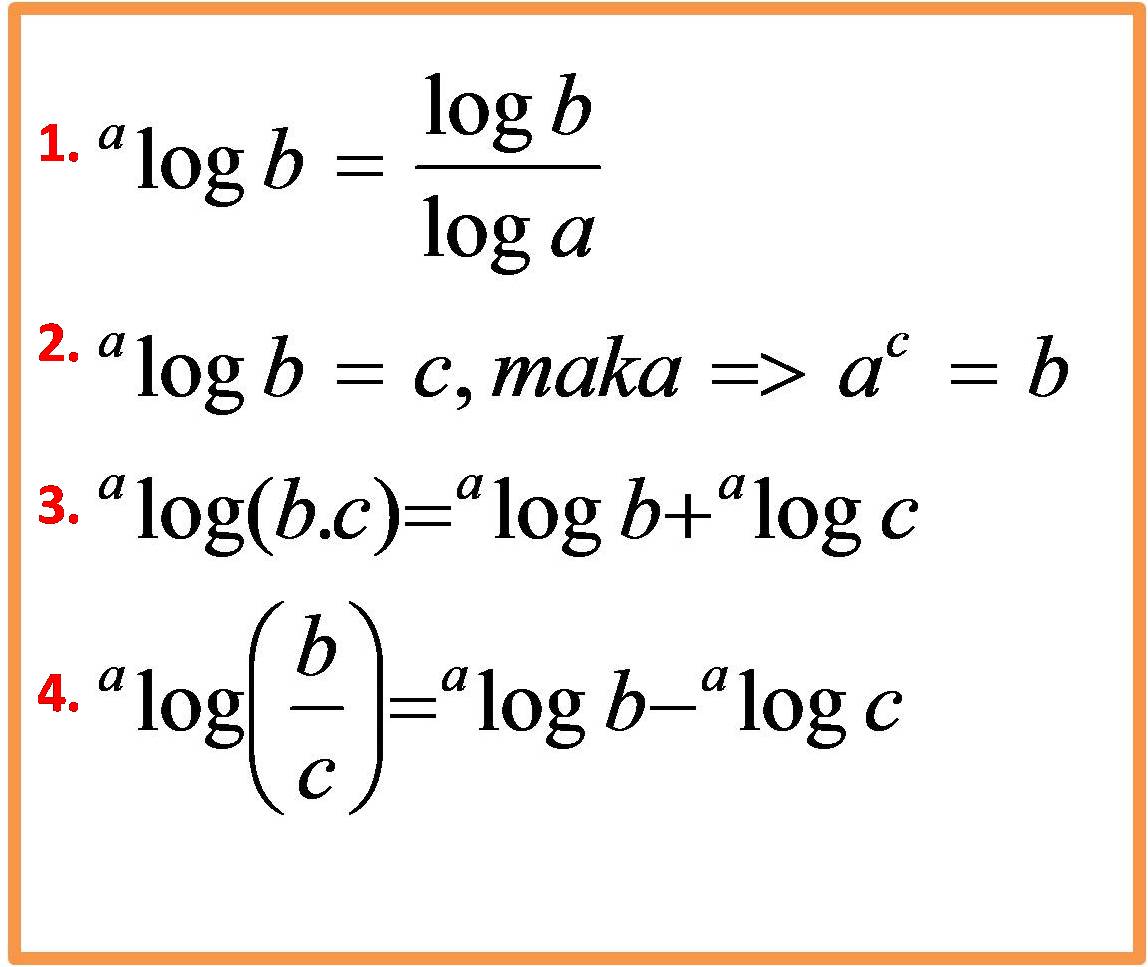
Sifatsifat Logaritma De Eka
Dalam astronomi, magnitudo yang mengukur terangnya bintang dengan menggunakan skala logaritmik, karena mata manusia mempersepsikan terang secara logaritmik. Bentuk Umum Logaritma Dalam penulisan logaritma a disebut bilangan pokok logaritma. Perhatikan bahwa a harus positif dan ≠1. Untuk dapat mengerjakan soal logaritma dengan lancar, kita perlu pahami dulu beberapa sifat logaritma penting berikut ini: Setelah memahami sifat-sifat logaritma di atas, mari kita ke contoh soal dan pembahasan logaritma berikut ini: Contoh 1: Jika 25log52x = 8 25 log 5 2 x = 8, maka x = ⋯ x = ⋯ 1/4 1/2 6 8 10 Pembahasan » Contoh 2:
Logaritma perkalian dua bilangan sama dengan jumlah logaritma dari masing-masing bilangan. a log (b×c)= a log b+ a log c Bukti: Misal a log b=x maka a x =b a log c=y maka a y =c b×c=a x ×a y dengan menggunakan aturan pangkat, diperoleh b×c=a x+y menurut definisi logaritma bentuk terakhir menjadi a log (b×c)=x+y ganti x dan y dengan pemisalan awal Secara sederhananya saja, logaritma bisa diartikan sebagai suatu invers atau kebalikan dari pemangkatan yang digunakan dalam menentukan besaran pangkat pada sebuah bilangan pokok. Sehingga intinya bahwa dengan Anda mempelajari ilmu logaritma, maka Anda akan bisa mencari besaran pangkat dari suatu bilangan yang telah diketahui hasil pangkatnya.

Contoh Soal Fungsi Logaritma Asli Dan Penyelesaiannya
Aturan hasil kali logaritma. Logaritma dari perkalian x dan y adalah jumlah dari logaritma dari x dan logaritma dari y. log b ( x ∙ y) = log b ( x) + log b ( y) Sebagai contoh: log 10 (3 ∙ 7) = log 10 (3) + log 10 (7) Aturan hasil bagi logaritma. Logaritma dari pembagian x dan y adalah selisih logaritma dari x dan logaritma y. Konsep logaritma ini berhubungan dengan konsep pangkat atau eksponen. Sebuah pangkat biasa ditulis sebagai a n, a disebut sebagai bilangan pokok atau basis sedangkan n disebut pangkat atau eksponen.Nilai dari a n bisa kita dapatkan secara langsung dengan mudah.Sebagai contoh 2 3 = 8; 3 2 = 9; 3 4 = 81; dan sebagainya. Bagaimana kalau persoalannya dibalik.