Statistical Tables for Students Binomial Table 1 Binomial distribution — probability function p x 0.01 0.05 0.10 0.15 0.20 0.25 .300.35 .400.45 0.50 How to Read a Binomial Distribution Table. Binomial Distribution Table. This binomial distribution table has the most common cumulative probabilities listed for n. Homework or test problems with binomial distributions should give you a number of trials, called n. Click the link below that corresponds to the n from your problem to take you to.

How To Use Binomial Probability Table Riviera Youlat
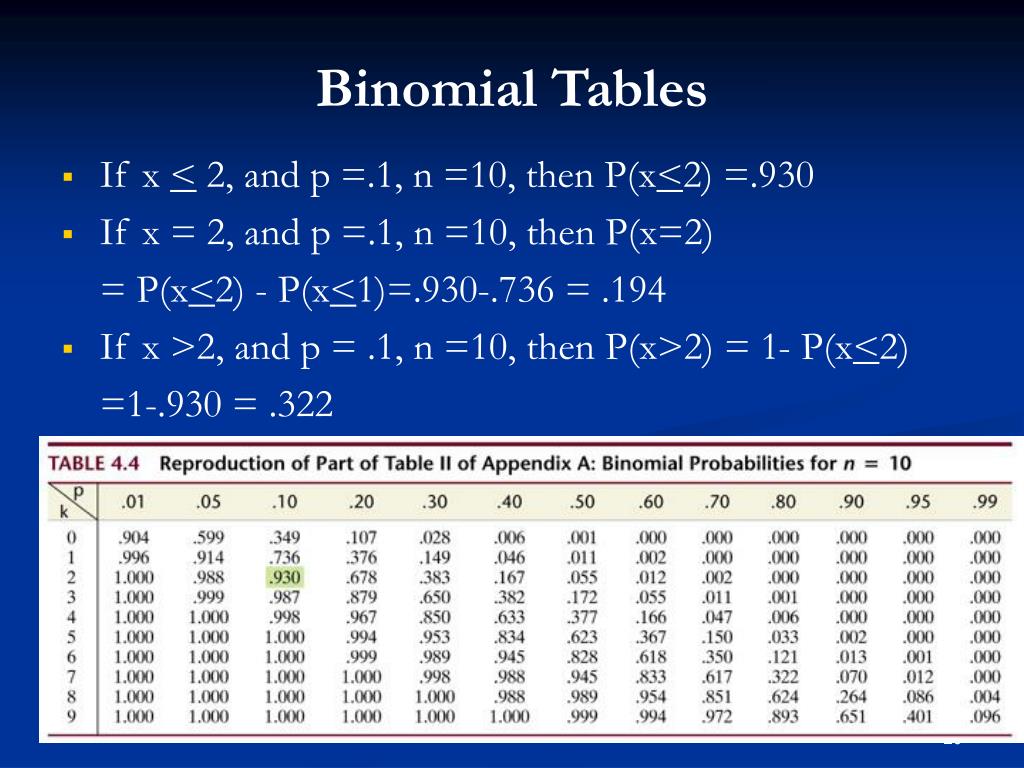
The binomial distribution table is a table that shows probabilities associated with the binomial distribution.To use the binomial distribution table, you only need three values: n: the number of trials r: the number of "successes" during n trials p: the probability of success on a given trial Using these three numbers, you can use the binomial distribution table to find the probability of. Binomial Probability Distribution Table This table shows the probability of x successes in n independent trials, each with probability of success p. n x 0.01 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 Table 4 Binomial Probability Distribution C p r qn − r n, r This table shows the probability of r successes in n independent trials, each with probability of success p. The table entries represent the area under the standard normal curve from 0 to the specified value of z. Binomial Distribution Table p n x 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.95 1 2

Download Binomial Probability Distribution Table N 20 Gantt Chart
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments,. In creating reference tables for binomial distribution probability, usually the table is filled in up to n/2 values. Other Tables . For other binomial distribution tables: n = 7 to 9, n = 10 to 11. For situations in which np and n(1 - p) are greater than or equal to 10, we can use the normal approximation to the binomial distribution. In this case, the approximation is very good and does not require the calculation of binomial coefficients. The binomial table is used to perform nonparametric tests on statistics that are distributed according to binomial distribution, especially the sign test and the binomial test. The National Bureau of Standards (1950) published individual and cumulative binomial distribution probabilities for \( { n \leq 49 } \), while cumulative binomial distribution probabilities for \( { n\!\!\leq\!\!1000. 11 Using Binomial Tables Even for a relatively small value of n, the computation of binomial probabilities can be tedious. Appendix Table A.1 tabulates the cdf F(x) = P(X x) for n = 5, 10, 15, 20, 25 in combination with selected values of p. Various other probabilities can then be calculated using the

Peter's Statistics Crash Course
Tabl e: Cumulative Binomial probabilities 1 [ ] ∑ ( ) − − ≤ = c x p nx x n P X c 0 1 p c 0.05 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 0.95 Therefore, we plug those numbers into the Binomial Calculator and hit the Calculate button. The calculator reports that the binomial probability is 0.193. That is the probability of getting EXACTLY 7 Heads in 12 coin tosses. (The calculator also reports the cumulative probabilities.
To find each of these probabilities, use the binomial table, which has a series of mini-tables inside of it, one for each selected value of n. To find P ( X = 0), where n = 11 and p = 0.4, locate the mini-table for n = 11, find the row for x = 0, and follow across to where it intersects with the column for p = 0.4. This value is 0.004. The outcomes of a binomial experiment fit a binomial probability distribution. The random variable X = the number of successes obtained in the n independent trials. The mean, μ, and variance, σ2, for the binomial probability distribution are μ = np and σ2 = npq. The standard deviation, σ, is then σ = npq−−−√ n p q.
PPT Chapter 4 PowerPoint Presentation, free download ID726350
The binomial distribution describes the probability of obtaining k successes in n binomial experiments. If a random variable X follows a binomial distribution, then the probability that X = k successes can be found by the following formula: P (X=k) = nCk * pk * (1-p)n-k. where: n: number of trials. k: number of successes. To understand how cumulative probability tables can simplify binomial probability calculations. To learn how to read a standard cumulative binomial probability table. To learn how to determine binomial probabilities using a standard cumulative binomial probability table when \(p\) is greater than 0.5.




