Eksplorasi, Ayo Temukan Garis Tegak Lurus || Matematika Kelas 4 SD/Mi Jika dua garis lurus berpotongan pada sudut siku-siku, maka kedua garis lurus tersebut disebut tegak lurus. Sekalipun dua garis lurus tidak berpotongan, tapi disaat salah satu garis lurus dipanjangkan akan memotong garis lurus lainnya pada sudut siku-siku, maka itu dikatakan sebagai tegak lurus. 1. Ayo, eksplorasi segiempat pada E halaman 56.

VIDEO EKSPLORASI KEDUDUKAN DUA GARIS LURUS YouTube
dilakukan uji eksplorasi garis resisten pada data yang telah disediakan berikut ini. Dapat dilihat, bahwa data tersebut tidak terlalu signifikan menunjukkan garis lurus, sehingga untuk mendapatkan garis resisten yang cocok, maka kita harus menentukkan data diatas apakah perlu dilakukan transformasi atau tidak. cara mengeksplorasi persamaan garis lurus menggunakan aplikasi komputer, Geogebra Modul ini berisi materi tentang pengenalan geogebra, membuat objek bangun datar, sudut, garis sejajar, garis tegak lurus, garis singgung dan lingkaran, eksplorasi perintah, persamaan, pertidaksamaan dan grafik fungsi, dan transformasi geometri. Ekspektasi Mengenai Garis Lurus. Ekspektasi Mengenai Garis Lurus. Aulia Yeru. 2017, JURNAL RUPA.
.jpg)
UNSUR RUPA Ms.Tabita Journal
persamaan garis yang mencakup garis sejajar, tegak lurus, bersilangan, dan gradien. Etnomatematika merupakan salah satu solusi bentuk pembelajaran matematika yang bermakna (Badrullah, 2020). Kata Kunci modul Learning Cycle lima fase fase eksplorasi persamaan garis lurus. Dalam pembelajaran matematika. siswa cenderung memahami konsep secara prosedural. Siswa mengerjakan soal-soal dengan cara-cara prosedural tanpa memahami bagaimana prosedur tersebut bekerja. Hal ini menyebabkan siswa mengalami kesulitan ketika dihadapkan dengan soal-soal dengan tipe berbeda. Tentukan persamaan garis lurus jika diketahui informasi berikut ini: Memiliki gradien = 3. Melalui titik (2, 1) Nah, untuk menjawab soal di atas, ada dua cara nih yang bisa elo lakukan. Cara pertama, elo bisa menggunakan rumus persamaan garis lurus seperti di bawah ini. y - 1 = 3 (x - 2) y = 3x - 6 + 1. y= 3x - 5. Ayo, temukan garis-garis yang sejajar pada segiempat di halaman 60. Garis a dan b saling sejajar. ① Carilah besarnya sudut f, g , h, dan i. Sudut f 110°, sudut g 180° - 110° = 70°, sudut h = g yaitu 70°, sudut i = sudut h yaitu 70°. ② Carilah panjang garis CD. CD = AB yaitu 2 cm. 4.

Eksplorasi Garis 1 YouTube
2.1 Pendahuluan Persamaan garis lurus sangat mudah dibuat, karena terdapat rumus baku untuk membuat persamaan yaitu dengan menghitung koefisien a dan b. Masalahnya adalah jika pola pencaran data (xi,yi) ternyata tidak mengikuti pola garis lurus atau memencar secara tidak beraturan, maka koefisien garis a dan b menjadi tidak relevan lagi untuk. Padahal, materi persamaan garis lurus ini dapat menjadi salah satu pintu masuk untuk melatihkan keterampilan berpikir tingkat tinggi dan materinya merupakan syarat untuk materi matematika yang.
Peserta didik melakukan eksplorasi, dimana mereka juga diharapkan mengaitkan dengan kehidupan nyata.. tertentu dan tegak lurus garis lain serta menentukan persamaan-persamaan linear yang melalui satu titik tertentu dan tegak lurus garis lain. Guru memberikan apresiasi atas partisipasi semua peserta didik Kegiatan Penutup (10 menit) Guru. uji eksplorasi garis resisten pada data yang telah disediakan berikut ini. Dapat dilihat, bahwa data tersebut tidak terlalu signifikan menunjukkan garis lurus, sehingga untuk mendapatkan garis resisten yang cocok, maka kita harus menentukkan data diatas apakah perlu dilakukan transformasi atau tidak. Untuk melihat perlu atau tidaknya
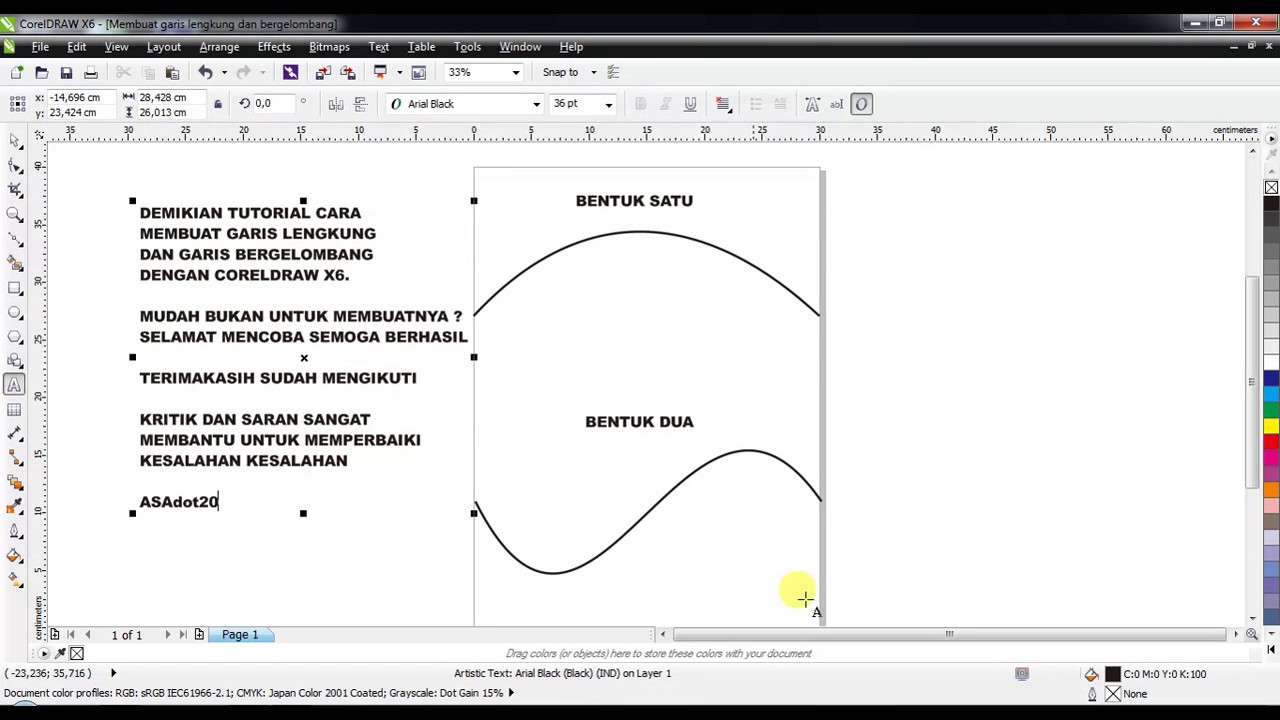
Eksplorasi Garis Lurus Dan Lengkung
Dalam video ini kami ingin menunjukan bentuk umum dari persamaan garis lurus. Persamaan garis lurus memiliki 2 bentuk umum yaitu eksplisit dan implisit. pa. Persamaan yang menggambarkan garis lurus dengan titik potong x a dan titik potong y b adalah (x/a) + (y/b) = 1. Jika Anda memiliki persamaan garis dalam bentuk umumnya, yaitu ax + by = c, dan nilai c tidak sama dengan 0. Maka Anda dapat menghitung titik potong x sebagai -c/a dan titik potong y sebagai -c/b.

.jpg)


