In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . The Rule The Fibonacci Sequence can be written as a "Rule" (see Sequences and Series ). First, the terms are numbered from 0 onwards like this: So term number 6 is called x6 (which equals 8). So we can write the rule: The Rule is xn = xn−1 + xn−2 where: xn is term number "n" xn−1 is the previous term (n−1) xn−2 is the term before that (n−2)

golden ratio, Fibonacci sequence, Mathematics HD Wallpapers / Desktop
That is, Phi is a geometric construction (concerning the properties of figures) that occurs as follows: Phi shown as a line divided in two segments, a and b, so that the whole line (a+b) is to the longer segment a the same as a is to the shorter segment b φ = (a+b) / a = a / b / Image: Wikimedia commons Fibonacci (/ ˌ f ɪ b ə ˈ n ɑː tʃ i /; also US: / ˌ f iː b-/, Italian: [fiboˈnattʃi]; c. 1170 - c. 1240-50), also known as Leonardo Bonacci, Leonardo of Pisa, or Leonardo Bigollo Pisano ('Leonardo the Traveller from Pisa'), was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages". Discover a mathematical sequence that can be used to create the shape of a spiral. See how this pattern shows up in nature and art! It is an Irrational Number (meaning we cannot write it as a simple fraction), but more than that. it is as far as we can get from being near any fraction. Just being irrational is not enough Pi ( 3.14159265. ), which is also irrational. Unfortunately it has a decimal very close to 1/7 (= 0.142857.), so it ends up with 7 arms.
Fibonacci sequence Gcse photography Briar CURLEY
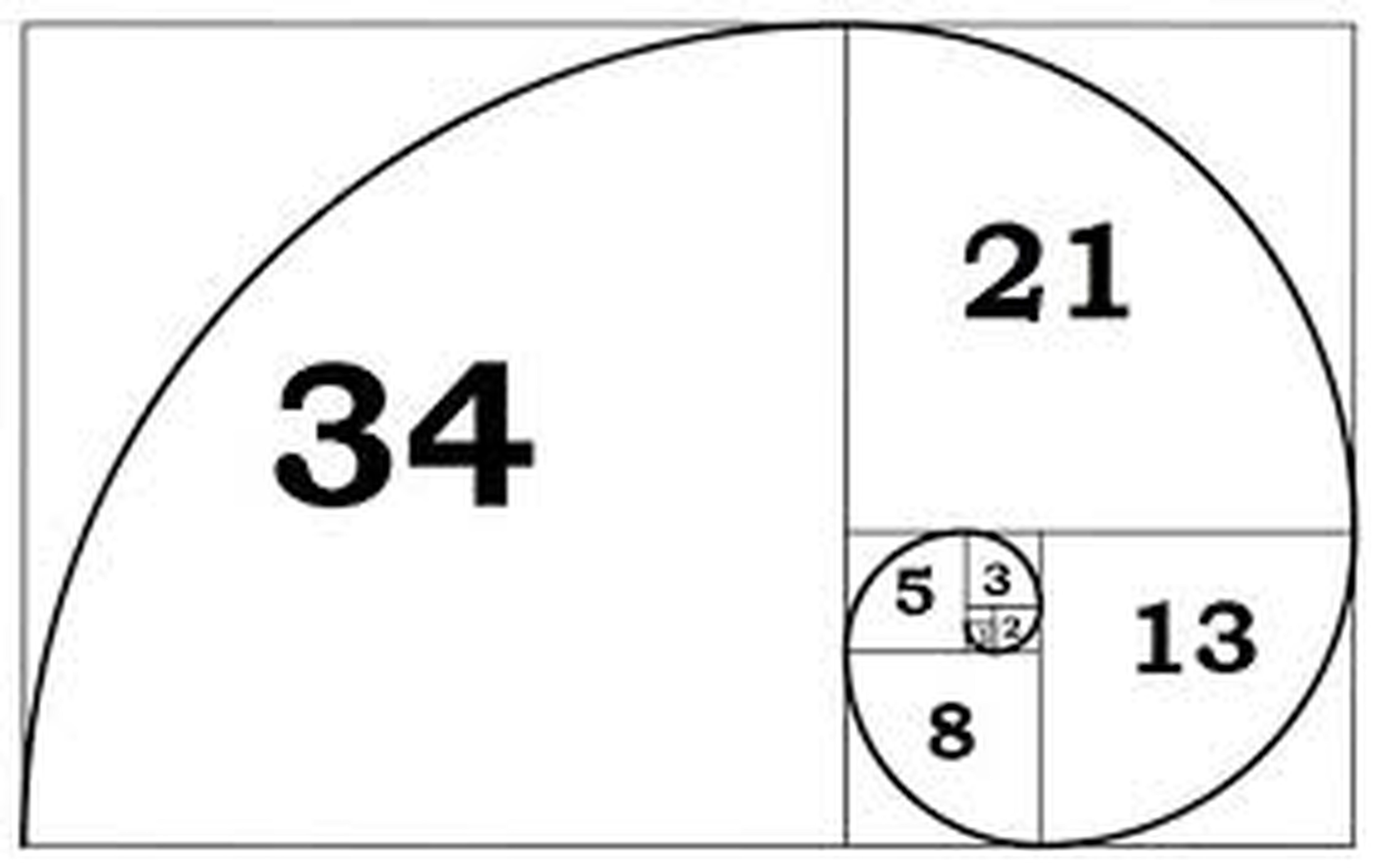
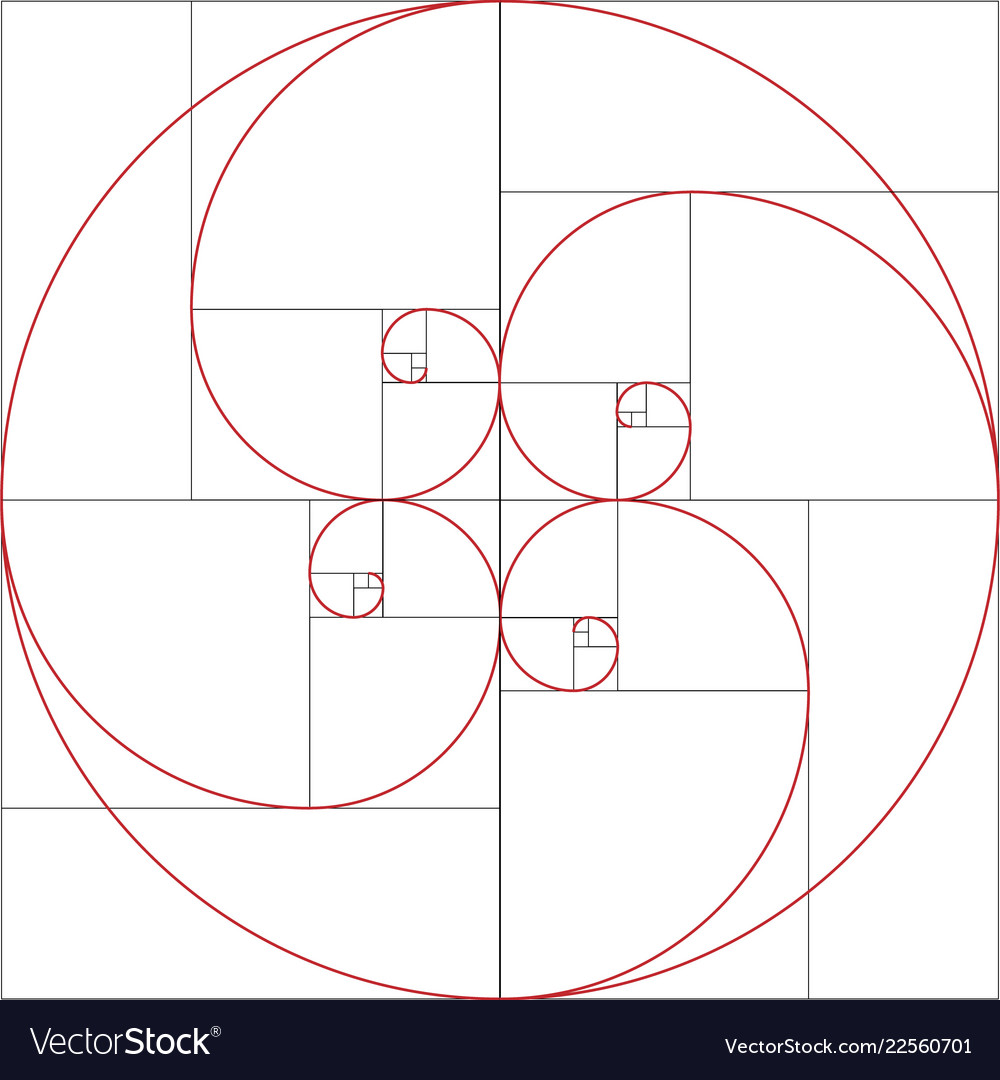
Fibonacci (born c. 1170, Pisa?—died after 1240) medieval Italian mathematician who wrote Liber abaci (1202; "Book of the Abacus"), the first European work on Indian and Arabian mathematics, which introduced Hindu-Arabic numerals to Europe. His name is mainly known because of the Fibonacci sequence. Fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21,., each of which, after the second, is the sum of the two previous numbers; that is, the n th Fibonacci number Fn = Fn − 1 + Fn − 2. The Golden Ratio has the decimal approximation of \ (\phi=1.6180339887\). The Golden Ratio is a special number for a variety of reasons. It is also called the divine proportion and it appears in art and architecture. It is claimed by some to be the most pleasing ratio to the eye. The Fibonacci sequence is an integer sequence defined by a simple linear recurrence relation. The sequence appears in many settings in mathematics and in other sciences. In particular, the shape of many naturally occurring biological organisms is governed by the Fibonacci sequence and its close relative, the golden ratio. The first few terms are.
Fibonacci spiral golden ratio Royalty Free Vector Image
Fibonacci Sequence. The Fibonacci sequence is a list of numbers. Start with 1, 1, and then you can find the next number in the list by adding the last two numbers together. The resulting (infinite) sequence is called the Fibonacci Sequence. Since we start with 1, 1, the next number is 1+1=2. We now have 1, 1, 2. The Fibonacci sequence has several interesting properties. 1) Fibonacci numbers are related to the golden ratio. Any Fibonacci number can be calculated (approximately) using the golden ratio, F n = (Φ n - (1-Φ) n )/√5 (which is commonly known as "Binet formula"), Here φ is the golden ratio and Φ ≈ 1.618034.
The Fibonacci numbers are the sequence of numbers defined by the linear recurrence equation (1) with . As a result of the definition ( 1 ), it is conventional to define . The Fibonacci numbers for , 2,. are 1, 1, 2, 3, 5, 8, 13, 21,. (OEIS A000045 ). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials with . Leonardo Pisano Fibonacci (1170-1240 or 1250) was an Italian number theorist. He introduced the world to such wide-ranging mathematical concepts as what is now known as the Arabic numbering system, the concept of square roots, number sequencing, and even math word problems. Fast Facts: Leonardo Pisano Fibonacci

Fibonacci Keith Critchlow Sacred geometry, Geometry art, Geometric
The Fibonacci sequence exhibits a certain numerical pattern which originated as the answer to an exercise in the first ever high school algebra text. This pattern turned out to have an interest and importance far beyond what its creator imagined. It can be used to model or describe an amazing variety of If we take three consecutive points from the Fibonacci sequence, and regard them as an integer triple thus, (F n-1,F n,F n + 1), we can at once move from regarding the Fibonacci sequence as a sequence of points on a number line to viewing it as a sequence of vectors in 3-dimensional space.From this viewpoint, we can quickly develop geometric ideas and spacial concepts directly related to.




