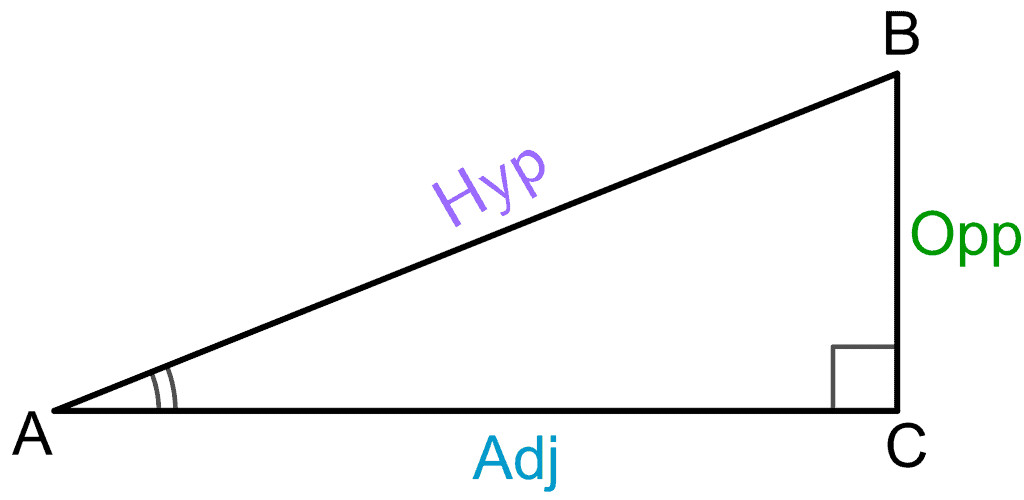
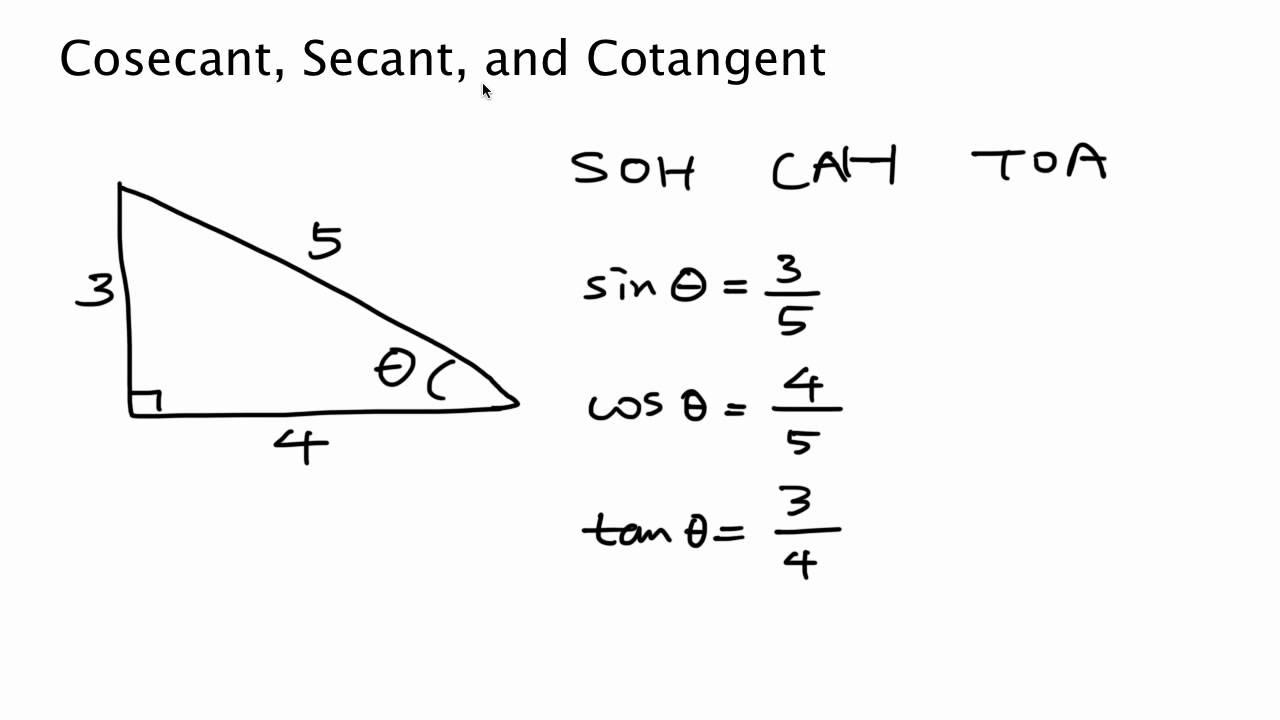Google Classroom. Learn how cosecant, secant, and cotangent are the reciprocals of the basic trig ratios: sine, cosine, and tangent. We've already learned the basic trig ratios: sin ( A) = a c cos ( A) = b c tan ( A) = a b A C B b a c. But there are three more ratios to think about: Instead of a c. . Secant Cosecant Cotangent - Explanation & Examples. Secant, cosecant, and cotangent are trigonometric functions derived from the three elementary functions sine, cosine, and tangent. This article will explain secant, cosecant, and cotangent functions, calculate them, find their signs, and finally give several examples with explanations.
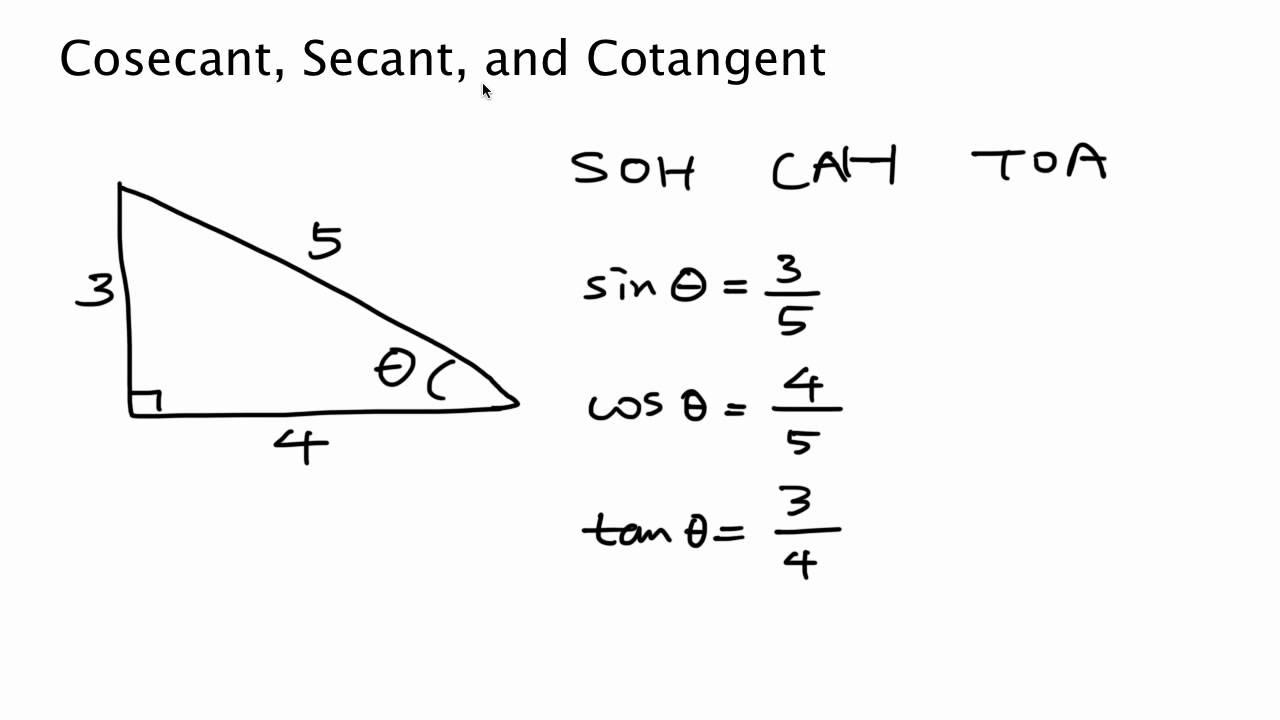
Trigonometric Functions Cosecant, Secant, and Cotangent YouTube
Worked example where we walk through finding the major trig ratiosPractice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/mat. Cosecant is the reciprocal of sine. Secant is the reciprocal of cosine. Cotangent is the reciprocal of tangent. When solving right triangles the three main identities are traditionally used. However, the reciprocal functions (secant, cosecant and cotangent) can be helpful in solving trig equations and simplifying trig identities. Related Links: We can do this using the Pythagorean Theorem: 52 + 122 = H2 25 + 144 = H2 169 = H2 H = 13. Now we can find the secant, cosecant, and cotangent of angle B: secB = hypotenuse adjacent side = 13 12 cscB = hypotenuse opposite side = 13 5 cotB = adjacent side opposite side = 12 5. 2. Find the secant, cosecant, and cotangent of angle A. Cofunction identities Sine and cosine, secant and cosecant, tangent and cotangent; these pairs of functions satisfy a common identity that is sometimes called the cofunction

PPT Ratios of Complementary Angles and Trigonometric Cofunctions
The abbreviation of cosecant is csc or cosec. The cotangent function is the reciprocal of the tangent function. The abbreviation of cotangent is cot. The following diagram shows the Reciprocal Trigonometric Functions. Scroll down the page for more examples and solutions on how to use the reciprocal trigonometric functions. The cosecant ( ), secant ( ) and cotangent ( ) functions are 'convenience' functions, just the reciprocals of (that is 1 divided by) the sine, cosine and tangent. So. Notice that cosecant is the reciprocal of sine, while from the name you might expect it to be the reciprocal of cosine! Everything that can be done with these convenience. Secant and Cosecant. Since secant is the inverse of cosine the graphs are very closely related. Figure \(\PageIndex{1}\) Notice wherever cosine is zero, secant has a vertical asymptote and where \(\cos x=1\) then \(\sec x=1\) as well. These two logical pieces allow you to graph any secant function of the form: Cosecant, Secant & Cotangent. mc-TY-cosecseccot-2009-1. In this unit we explain what is meant by the three trigonometric ratios cosecant, secant and cotangent. We see how they can appear in trigonometric identities and in the solution of trigonometrical equations. Finally, we obtain graphs of the functions cosec θ, sec θ and cot θ from.
Secant cosecant cotangent Explanation & Examples
Cotangent is the reciprocal trig function of tangent function and can be defined as cot θ = cos θ /sin θ. It is an odd function, meaning cot (− θ) = − cot (θ), and it has the property that cot (θ + π) = cot (θ). Because sine is the denominator, and the function is undefined when sin (θ) = 0, the cotangent graph has vertical. •One cycle occurs between and . • There are vertical asymptotes at each end of the cycle. The asymptote that occurs at repeats every π units. • period: π • amplitude: none, graphs go on forever in vertical directions. Note: a graphing utility (such as the one used to produce these graphs) may not show the function approaching infinity (going on forever upward or downward).
What are Cosecant, Secant and Cotangent? In our previous video about trigonometry we already discussed the three main trigonometric functions, sine, cosine,. Trigonometric functions, i.e. trig functions, are ratios of pairs of sides of a right triangle (i.e. a triangle that contains a 90° angle). The three sides of a right triangle are: the hypotenuse.
Secant cosecant cotangent Explanation & Examples
The range of cscx is the same as that of secx, for the same reasons (except that now we are dealing with the multiplicative inverse of sine of x, not cosine of x).Therefore the range of cscx is cscx ‚ 1 or cscx • ¡1: The period of cscx is the same as that of sinx, which is 2….Since sinx is an odd function, cscx is also an odd function. Finally, at all of the points where cscx is. A Level Maths revision tutorial video.For the full list of videos and more revision resources visit www.mathsgenie.co.uk.