A 1 = π r 12 for the area enclosed by C 1. A 2 = π r 22 for the area enclosed by C 2. A = A 1 - A 2 = π ( r 12 - r 22) for the area of the solid cross section of the tube, the end, an annulus . Volume, V, (using volume for a cylinder ): V 1 = π r 12 h for the volume enclosed by C 1. V 2 = π r 22 h for the volume enclosed by C 2. Solid Geometry . Solid Geometry is the geometry of three-dimensional space, the kind of space we live in. Three Dimensions. It is called three-dimensional, or 3D, because there are three dimensions: width, depth and height. Simple Shapes. Let us start with some of the simplest shapes:

Geometric Solids Chart
In Geometry, the shape or the figure that has three (even higher) dimensions are known as solids or three-dimensional shapes. The study of the properties, volume and surface area of three-dimensional shapes is called Solid Geometry. Let us go ahead and focus more on the study of geometrical solids. Solid geometry or stereometry is the geometry of three-dimensional Euclidean space (3D space). [1] A solid figure is the region of 3D space bounded by a two-dimensional surface; for example, a solid ball consists of a sphere and its interior . Solid geometry deals with the measurements of volumes of various solids, including pyramids, prisms. Many formulas are associated with the study of three-dimensional shapes in geometry. Here, you find formulas for calculating the volume, surface area, and lateral area of cylinders, cones, spheres, pyramids, cube, and rectangular prisms. We study Euclidean geometry to understand the fundamentals of geometry. Euclidean Geometry refers to the study of plane and solid figures on the basis of axioms (a statement or proposition) and theorems. The fundamental concepts of Euclidean geometry include Points and Lines, Euclid's Axioms and Postulates, Geometrical Proof, and Euclid's Fifth Postulate.
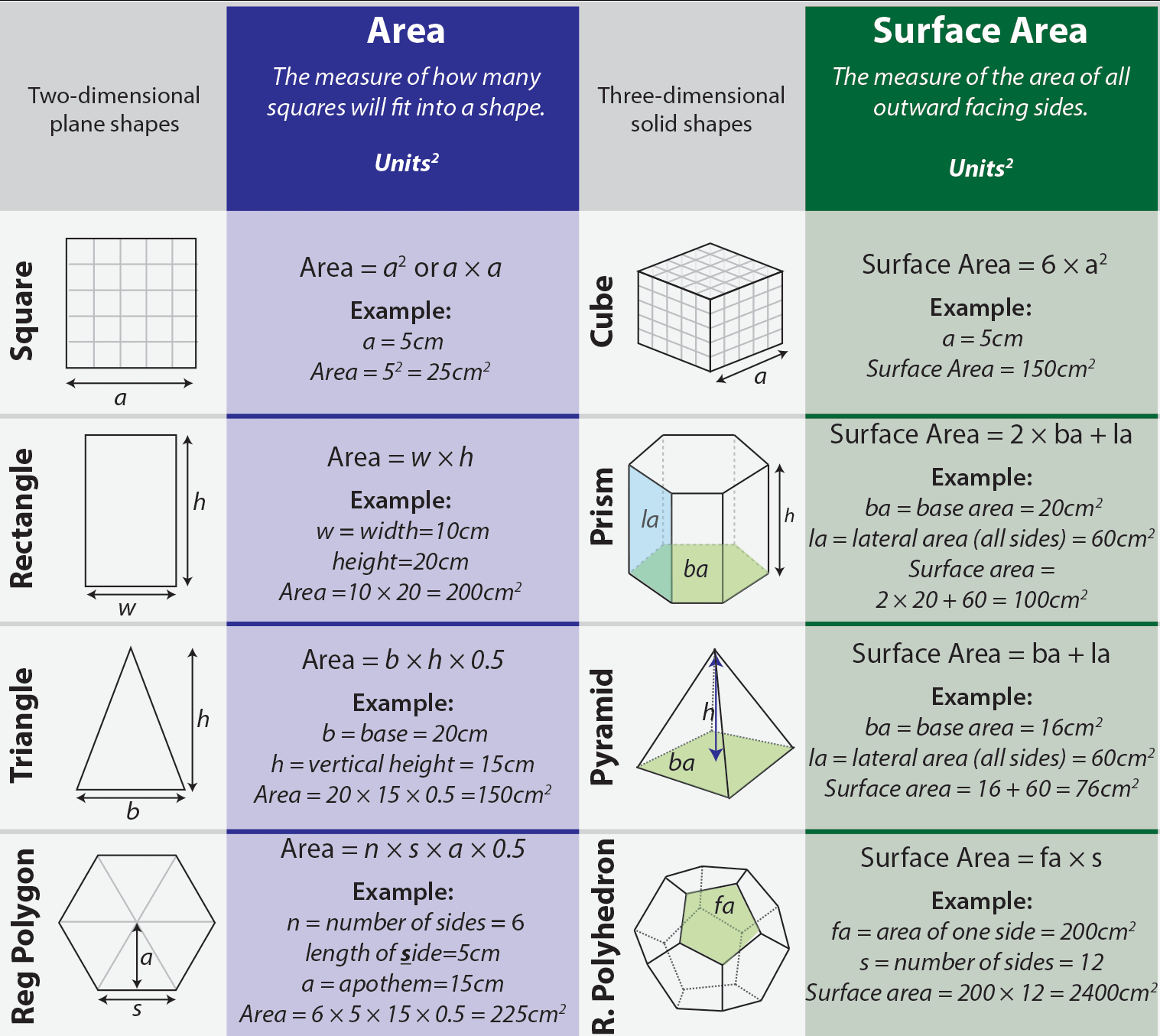
Important Surface Area Formulas Engineering Feed
Formulas in Solid Geometry. Formulas in Solid Geometry. Derivation of Formula for Lateral Area of Frustum of a Right Circular Cone. Derivation of Formula for Total Surface Area of the Sphere by Integration. Derivation of Formula for Volume of the Sphere by Integration. Derivation of formula for volume of a frustum of pyramid/cone. Solid geometry: Unit test; About this unit. Take your knowledge of geometry into new territory! In this unit, we'll explore three-dimensional shapes and all the fascinating properties they possess.. Volume formulas review (Opens a modal) Practice. Volume and surface area of cylinders Get 5 of 7 questions to level up! Apply volume of solids. Solid Geometry. That portion of geometry dealing with solids, as opposed to plane geometry. Solid geometry is concerned with polyhedra, spheres , three-dimensional solids, lines in three-space, planes , and so on. Applying the Formulas. You know how to identify the solids, and you also know the volume formulas for these solids. To calculate the actual volume of a given shape, all you need to do is substitute the solid's dimensions into the formula and calculate. In the examples below, notice that cubic units (meters 3, inches 3, feet 3) are used.
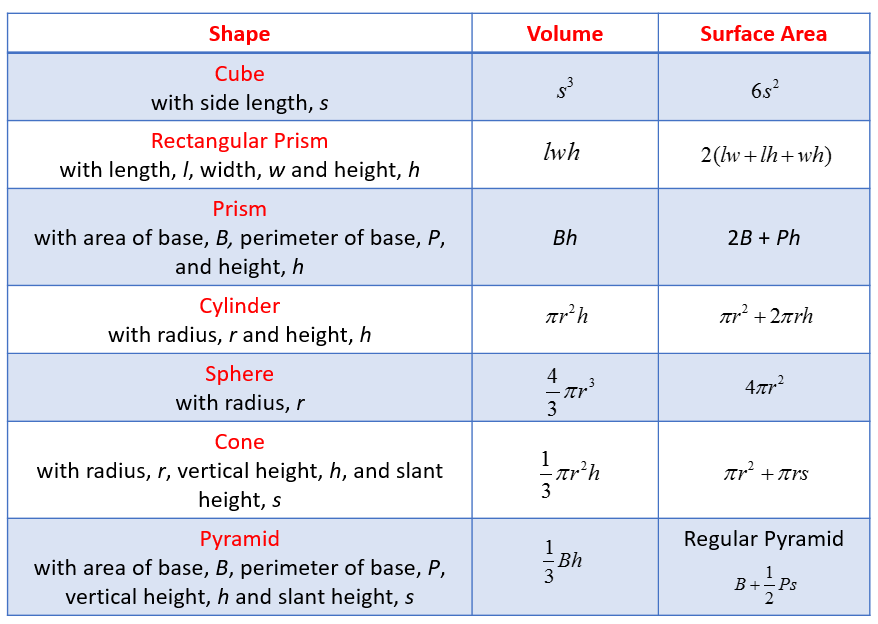
Solid Geometry Types of Solids (Formulas, Examples, Worksheets, Games
Solid geometry is concerned with three-dimensional shapes. Some examples of three-dimensional shapes are cubes, rectangular solids, prisms , cylinders, spheres, cones and pyramids. We will look at the volume formulas and surface area formulas of the solids. We will also discuss some nets of solids. Geometry. Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles. shapes that can be drawn on a piece of paper. Solid Geometry is about three dimensional objects like.
Geometry Formulas. Geometry formulas are used for finding dimensions, perimeter, area, surface area, volume, etc. of the geometric shapes. Geometry is a part of mathematics that deals with the relationships of points, lines, angles, surfaces, solids measurement, and properties. Finding Volumes of Some Common Geometric Objects. Example 1. Find the volume of the rectangular solid. Solution. VR = = = = l ⋅ w ⋅ h 9 in ⋅ 10 in. ⋅ 3 in 270 cu in 270 in3 V R = l ⋅ w ⋅ h = 9 in ⋅ 10 in. ⋅ 3 in = 270 cu in = 270 in 3. The volume of this rectangular solid is 270 cu in. Example 2. Find the approximate volume of.
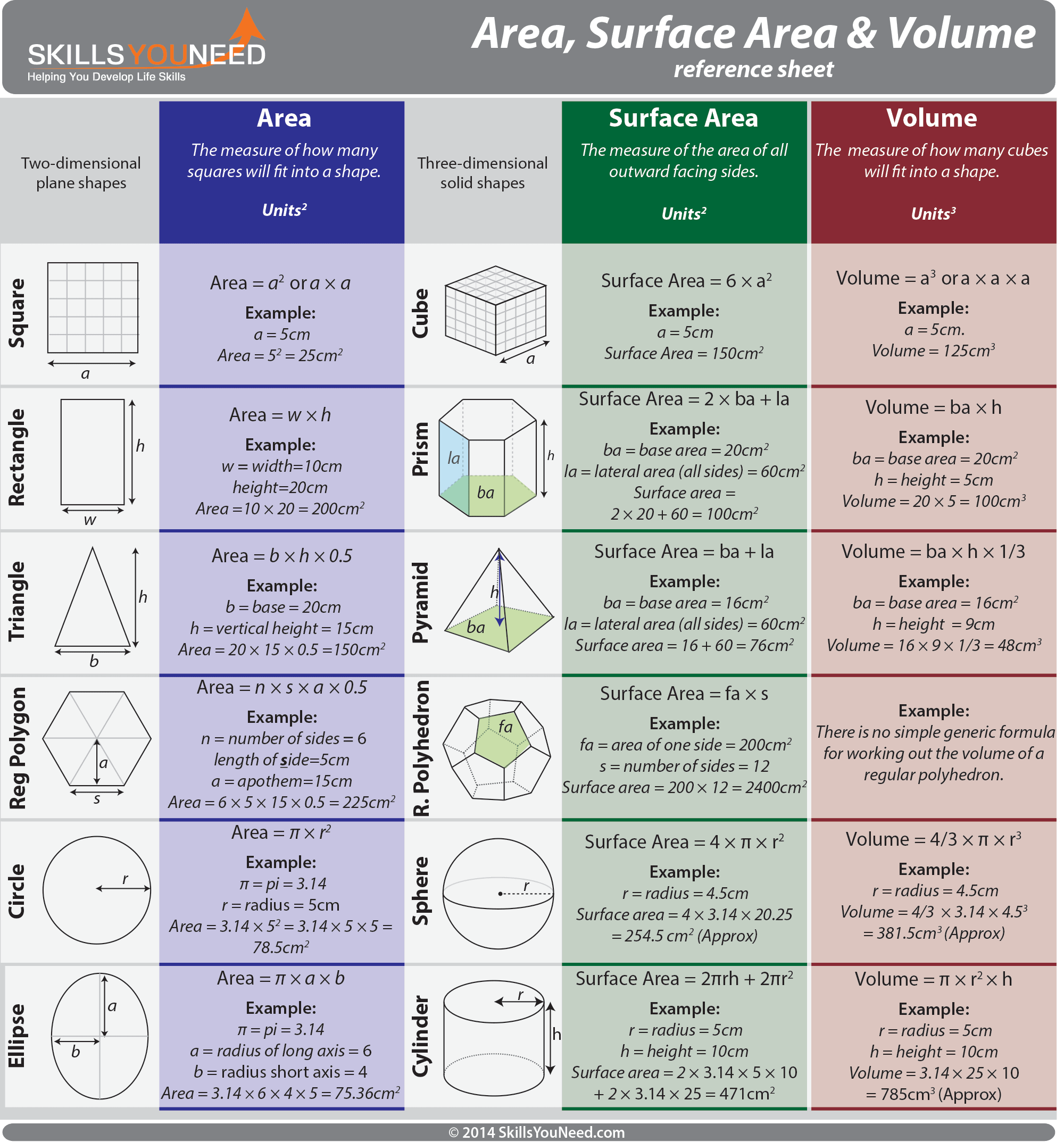
Area, Surface Area and Volume SkillsYouNeed
Prisms. A prism is a solid shape defined on a 3-dimensional plane with two identical shapes facing each other. The different types of prisms are triangular prisms, square prisms, pentagonal prisms, hexagonal prisms, etc. Prisms are also broadly classified into regular prisms and oblique prisms. Formulas of Solid Geometry. The volume of a geometric solid is the measure of the space it occupies.We express it in cubic units. The surface area of a geometric solid is the sum of the areas of all its surfaces or faces.We express it in square units. The formula for volume and surface area of a few common solid geometric shapes is given below:.




