Welcome to this trigonometric calculator, a trig tool created to: Calculate any trigonometric function by inputting the angle at which you want to evaluate it; and Solve for the sides or angles of right triangles by using trigonometry. Keep reading this article to learn more about trigonometric functions and the trig identities that relate them. Solution: tan 330° = tan (360 - 30)° = - tan 30°; since we know, tan (n ∙ 360° - θ) = - tan θ = - 1 √ 3 4. Find the value of cos 315°. Solution: cos 315° = cos (360 - 45)° = cos 45°; since we know, cos (n ∙ 360° - θ) = cos θ = 1 √ 2 Trigonometric Functions Basic Trigonometric Ratios and Their Names Restrictions of Trigonometrical Ratios
Trigonometry Table Up To 360
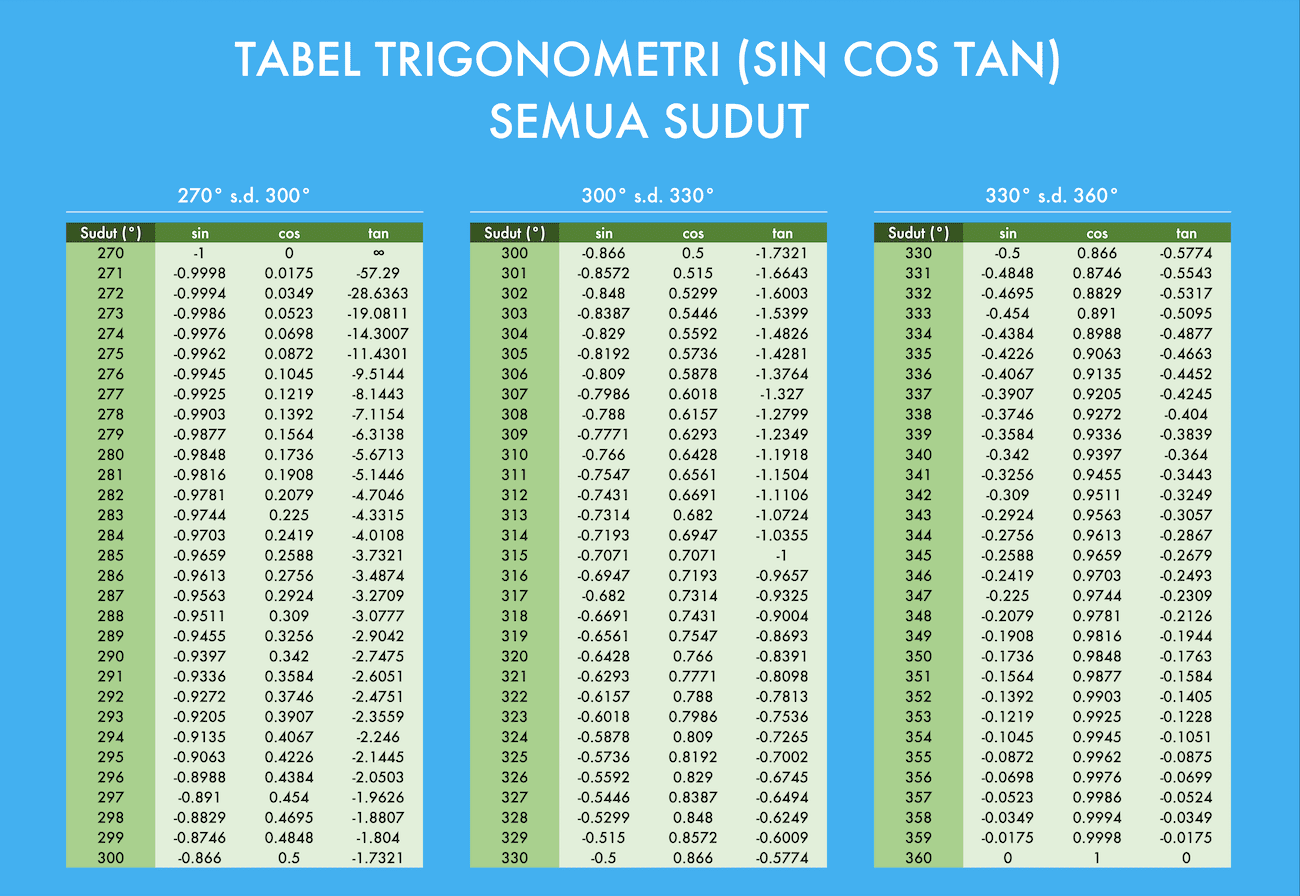
Search Trigonometric Tables ( Math | Trig | Tables) PI = 3.141592. (approximately 22/7 = 3.1428) radians = degrees x PI / 180 (deg to rad conversion) degrees = radians x 180 / PI (rad to deg conversion) Those with a zero in the denominator are undefined. They are included solely to demonstrate the pattern. In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) [1] [2] are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. The trigonometric values table from 0 to 360 lists the one-degree increment values of the sine (sin), cosine (cos), tangent (tan), cotangent (cot) functions. Sine 0 = 0.0 Cosine 0 = 1.0 Tangent 0 = 0.0 Cotangent 0 = ∞ Sine 1 = 0.0174524064373 Cosine 1 = 0.999847695156 Tangent 1 = 0.0174550649282 Cotangent 1 = 57.2899616308 The three basic trigonometric functions are: Sine (sin), Cosine (cos), and Tangent (tan). What is trigonometry used for? Trigonometry is used in a variety of fields and applications, including geometry, calculus, engineering, and physics, to solve problems involving angles, distances, and ratios. Show more Why users love our Trigonometry Calculator
Tabel Trigonometri Sin Cos Tan Lengkap Semua Sudut Cara Memahaminya 2020
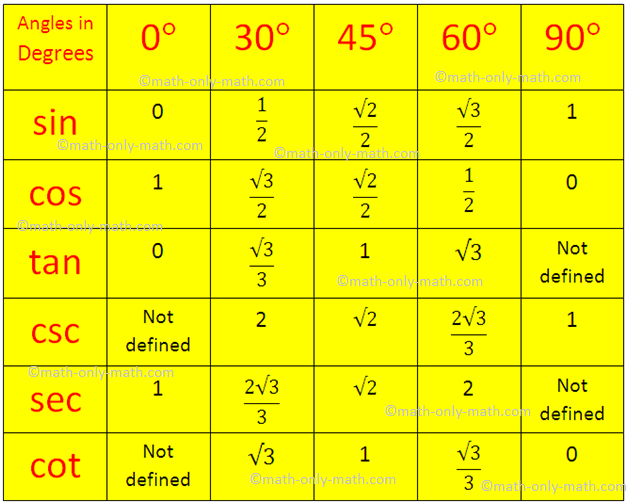
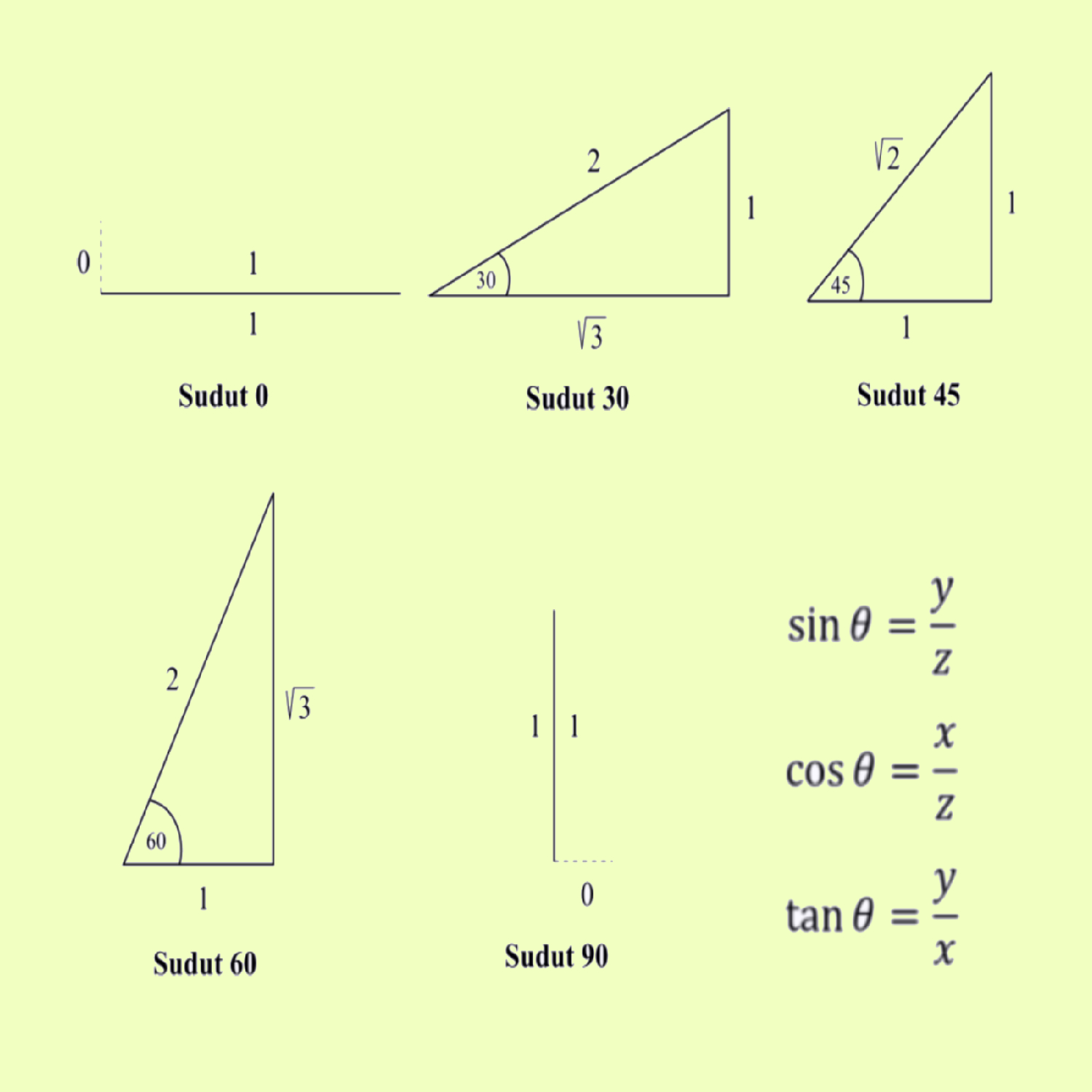
Sine, Cosine and Tangent The main functions in trigonometry are Sine, Cosine and Tangent They are simply one side of a right-angled triangle divided by another. For any angle " θ ": (Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.) Example: What is the sine of 35°? Using this triangle (lengths are only to one decimal place): Using trigonometry formulas, we can represent the sin 360 degrees as: ± √ (1-cos² (360°)) ± tan 360°/√ (1 + tan² (360°)) ± 1/√ (1 + cot² (360°)) ± √ (sec² (360°) - 1)/sec 360° 1/cosec 360° Note: Since 360° lies on the positive x-axis, the final value of sin 360° will be 0. We can use trigonometric identities to represent sin 360° as, Let's look at some problems involving angles greater than 360∘ 360 ∘. Find the value of the following expressions: 1. sin420∘ sin 420 ∘. sin420∘ = 3-√ 2 sin 420 ∘ = 3 2. 420∘ 420 ∘ is a full rotation of 360 degrees, plus an additional 60 degrees. Therefore the angle is coterminal with 60∘ 60 ∘, and so it shares the same. Click on the desired functions to find the individual degree table and their values calculator. These trigonometric ratios table values were essential for navigation, science and engineering. Trigonometry Table which gives the trigonometric ratios of standard angles 0°, 30°, 45°, 60° and 90° for Sin, Cos, Tan, Sec, Cot, Cosec functions.
Tabel Trigonometri Sin Cos Tan Lengkap Semua Sudut Cara Memahaminya 2020
Trigonometry (from Ancient Greek τρίγωνον (trígōnon) 'triangle', and μέτρον (métron) 'measure') [1] is a branch of mathematics concerned with relationships between angles and ratios of lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. [2] Solve Related Concepts Trigonometry Trigonometry is a branch of mathematics concerned with relationships between angles and ratios of lengths. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies.
The sum of the internal angles of a triangle will always be 360 ° 360\degree 360°. In a right triangle, there's a right angle (90 ° 90\degree 90°) and, therefore, the sum of the other two angles (α \alpha α and β \beta β) will be 90 ° 90\degree 90°. Therefore: Given β \beta β: α = 90 ° − β \alpha = 90\degree - \beta α = 90. Trigonometric table from 0 to 360 (cos -sin-cot-tan-sec-cosec) 6 Comments / By physicscatalyst / January 27, 2019 Trigonometric ratios are important module in Maths. Here in this post, I will provide Trigonometric table from 0 to 360 (cos -sin-cot-tan-sec-cosec) and also the easy and simple way to remember it.
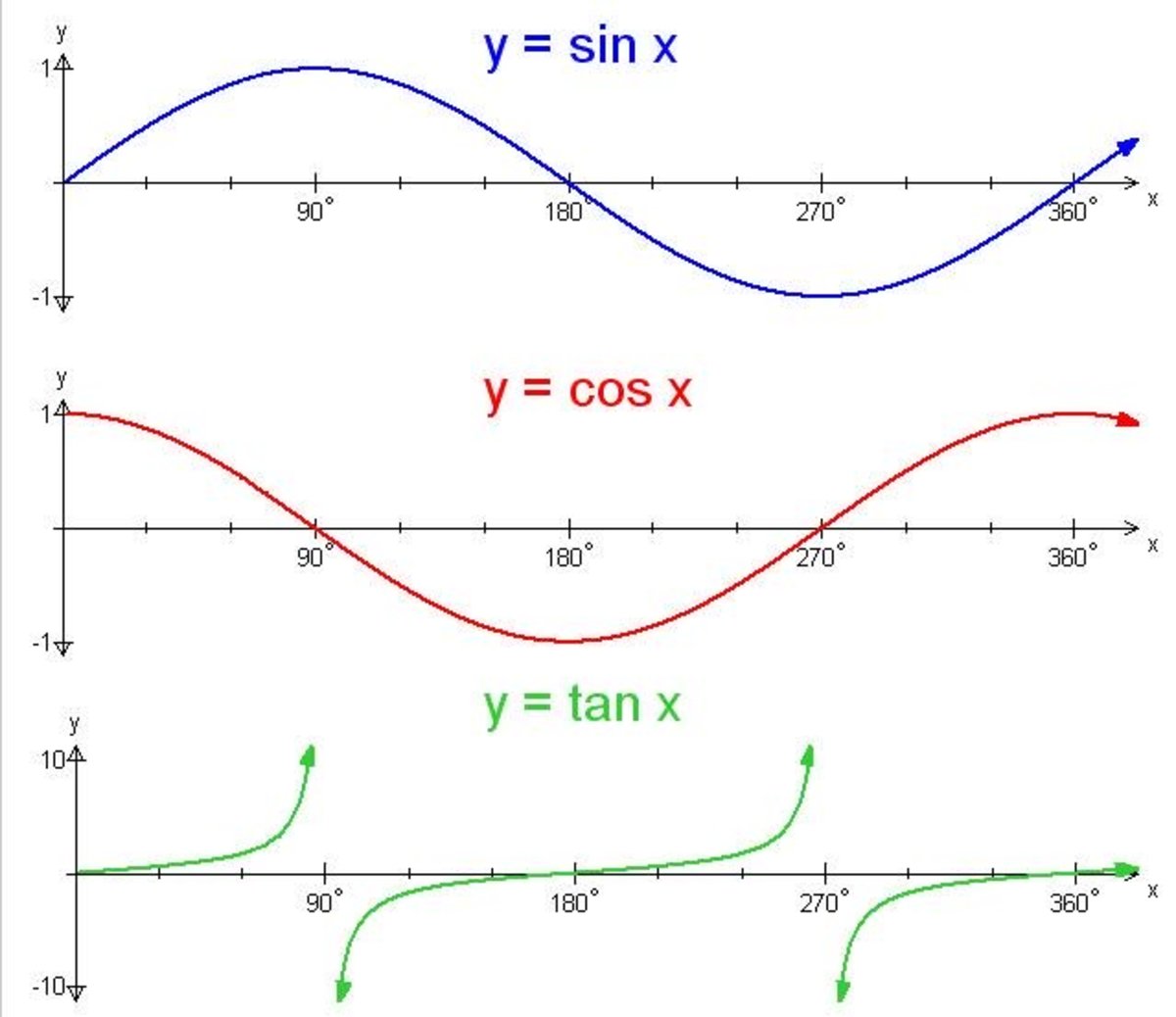
Trigonometry Graphing the Sine, Cosine and Tangent Functions Owlcation
Math Article Trigonometry Angles Trigonometry Angles The angles by which trigonometric functions can be represented are called as trigonometry angles. The important angles of trigonometry are 0°, 30°, 45°, 60°, 90°. These are the standard angles of trigonometric ratios, such as sin, cos, tan, sec, cosec, and cot. Trigonometric Functions. Trigonometric functions are the basic six functions that have a domain input value as an angle of a right triangle, and a numeric answer as the range.The trigonometric function (also called the 'trig function') of f(x) = sinθ has a domain, which is the angle θ given in degrees or radians, and a range of [-1, 1].




