Over 27,000 video lessons and other resources, you're guaranteed to find what you need. Learn faster. Stay motivated. Study smarter. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Graphs of the trigonometric functions | Desmos
Trigonometry Graphing the Sine, Cosine and Tangent Functions Owlcation
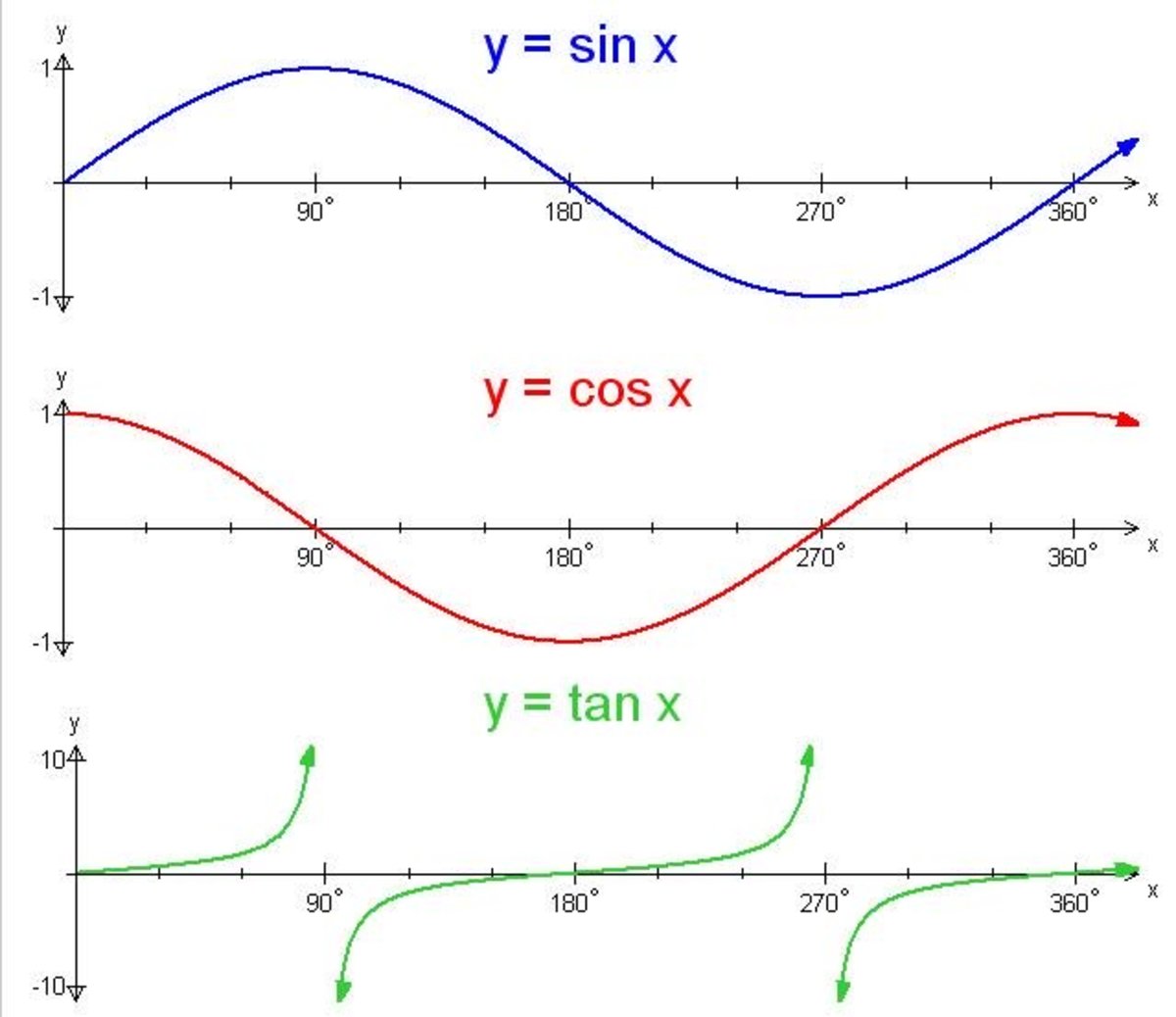
y = A sin(Bx − C) + D. y = A cos(Bx − C) + D. The graph could represent either a sine or a cosine function that is shifted and/or reflected. When x = 0, the graph has an extreme point, (0, 0). Since the cosine function has an extreme point for x = 0, let us write our equation in terms of a cosine function. Below are the graphs of the three trigonometry functions sin x, cos x, and tan x. In these trigonometry graphs, x-axis values of the angles are in radians, and on the y-axis, its f (x) is taken, the value of the function at each given angle. Sin Graph y = sin x The roots or zeros of y = sin x is at the multiples of π Start Course challenge Unit 1: Right triangles & trigonometry 0/700 Mastery points Ratios in right triangles Introduction to the trigonometric ratios Solving for a side in a right triangle using the trigonometric ratios This topic covers: - Unit circle definition of trig functions - Trig identities - Graphs of sinusoidal & trigonometric functions - Inverse trig functions & solving trig equations - Modeling with trig functions - Parametric functions Introduction to radians Learn Intro to radians Radians & degrees Degrees to radians Radians to degrees
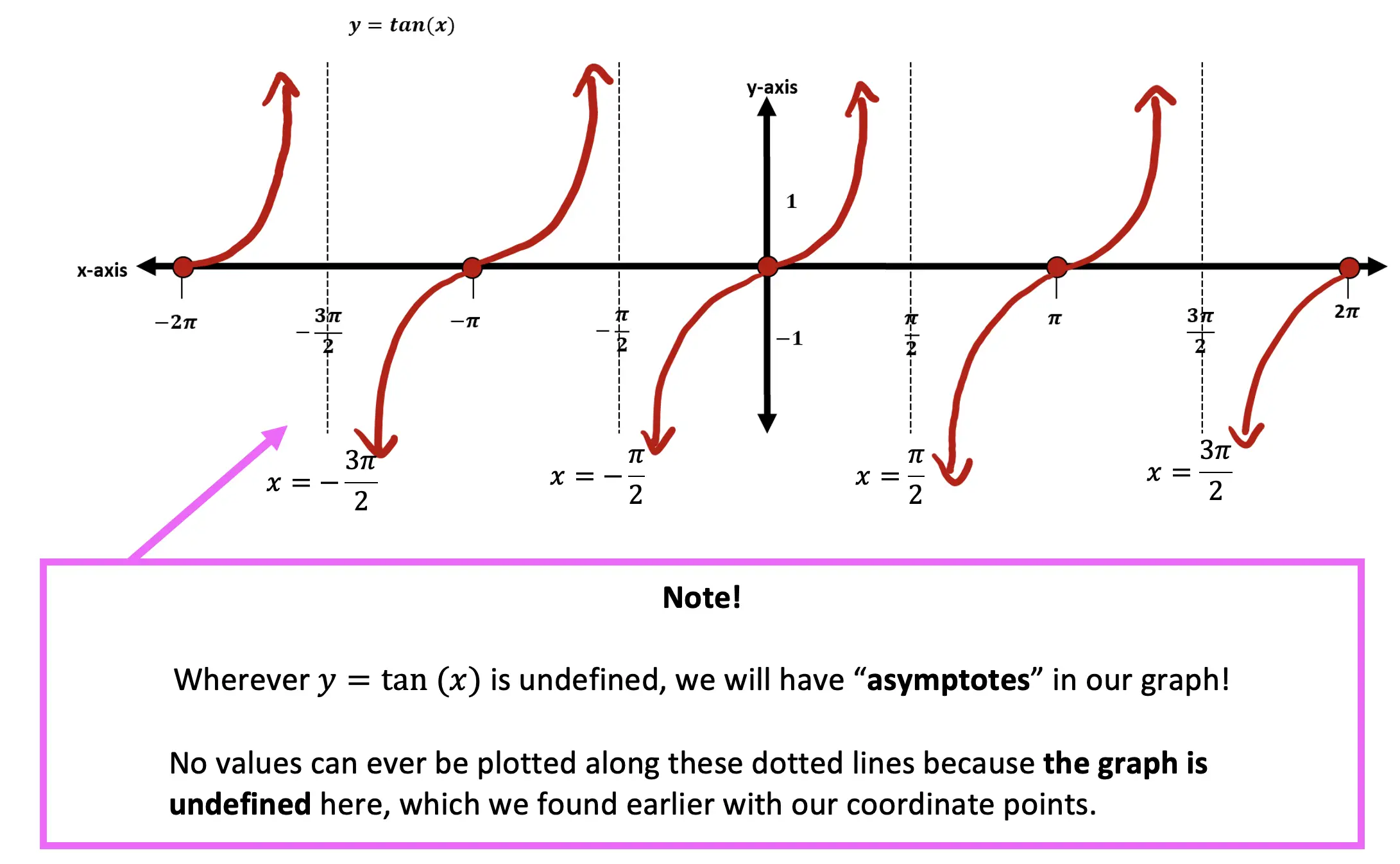
Graphing Trig Functions Algebra 2/Trig. Math Lessons
In graphing trigonometric functions, we typically use radian measure along the x -axis, so the graph would generally look like this: The graph of the standard sine function begins at the zero point, then rises to the maximum value of 1 between 0 and 7 3 radians. It then decreases back to 0 at. 1: Functions and Graphs 1.3: Trigonometric Functions Expand/collapse global location 1.3: Trigonometric Functions Graphs of Sine, Cosine and Tangent A sine wave made by a circle: A sine wave produced naturally by a bouncing spring: Plot of Sine The Sine Function has this beautiful up-down curve (which repeats every 2 π radians, or 360°). It starts at 0, heads up to 1 by π /2 radians (90°) and then heads down to −1. Plot of Cosine Using the Graphs of Trigonometric Functions to Solve Real-World Problems. Many real-world scenarios represent periodic functions and may be modeled by trigonometric functions. As an example, let's return to the scenario from the section opener. Have you ever observed the beam formed by the rotating light on a police car and wondered about the.

Graphs of Trigonometric Functions Meaning, Characteristics Embibe
We will describe a geometrical way to create the graph, using the unit circle. This is the circle of radius 1 in the x y -plane consisting of all points ( x, y) which satisfy the equation x 2 + y 2 = 1. Figure 2.3.1. We see in Figure 5.1.1 that any point on the unit circle has coordinates ( x, y) = ( cos θ, sin θ), where θ is the angle that. 1. Graphs of y = a sin x and y = a cos x, talks about amplitude. Amplitude is a indication of how much energy a wave contains. 2. Graphs of y = a sin bx and y = a cos bx introduces the period of a trigonometric graph. 3.
4 The trigonometric ratios sinθ and cosθ are functions of the angle θ. 5 The period of the sine function is 360 ∘. Its midline is the horizontal line y = 0, and the amplitude of the sine function is 1. 6 The graph of the cosine function has the same period, midline, and amplitude as the graph of the sine function. Trigonometric graphs can be sketched when you know the amplitude, period, phase and maximum and minimum turning points. Part of Maths Trigonometric skills Remove from My Bitesize In this guide.
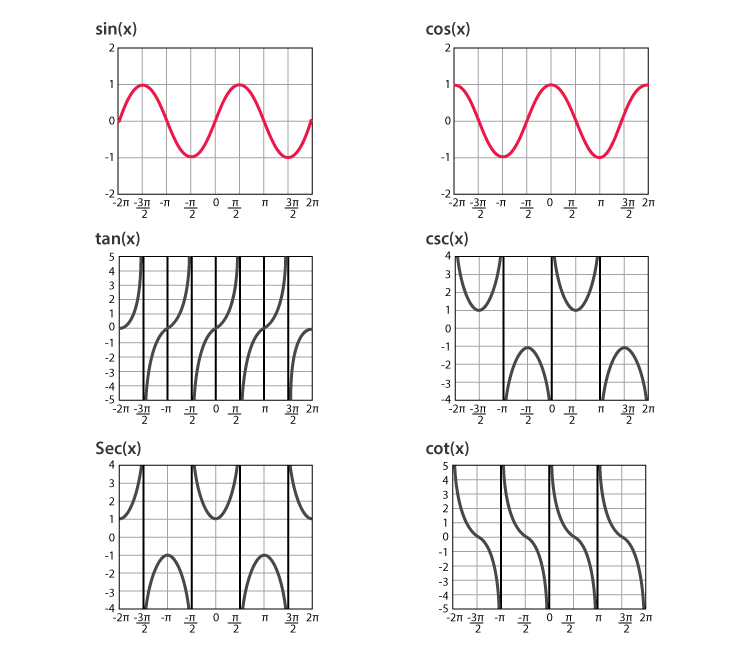
Six Trigonometric Functions Graph Examples
Video transcript. - [Instructor] We're told Alexa is riding on a Ferris wheel. Her height above the ground in meters is modeled by H of t where t is the time in seconds. And we can see that right over here. Now what I want to focus on this video is some features of this graph. And the features we're gonna focus on, actually the first of them. The symmetrical and periodic properties of the trigonometric graphs will give an infinite number of solutions to any trigonometric equation. Example Solve the equation \ (\sin {x} = 0.5\) for.




