Introduction Figures 1 through 32 provide a series of shear and moment diagrams with accompanying formulas for design of beams under various static loading conditions. Shear and moment diagrams and formulas are excerpted from the Western Woods Use Book, 4th edition, and are provided herein as a courtesy of Western Wood Products Association. This is a graphical representation of the variation of the bending moment on a segment or the entire length of a beam or frame. As a convention, the positive bending moments are drawn above the x -centroidal axis of the structure, while the negative bending moments are drawn below the axis.

Understanding Shear Force And Bending Moment Diagrams Engineering Discoveries
These reactions can be determined from free-body diagrams of the beam as a whole (if the beam is statically determinate), and must be found before the problem can proceed. For the beam of Figure 4: ∑Fy = 0 = −VR + P ⇒ VR = P ∑ F y = 0 = − V R + P ⇒ V R = P. The shear and bending moment at x x are then. V(x) = VR = P = constant V ( x. BEAM GURU .COM is a online calculator that generates Bending Moment Diagrams (BMD) and Shear Force Diagrams (SFD), Axial Force Diagrams (AFD) for any statically determinate (most simply supported and cantilever beams) and statically indeterminate beams, frames and trusses. Calculate shear force diagrams How to use SkyCiv Beam Calculator Welcome to our Free Beam Calculator! Our calculator generates the Reactions, Shear Force Diagrams (SFD), Bending Moment Diagrams (BMD), deflection, and stress of a cantilever beam or simply supported beam. 1. Calculate reactions at supports and draw Free Body Diagram (FBD) If you're not sure how to determine the reactions at the supports - please see this tutorial first. Once you have the reactions, draw your Free Body Diagram and Shear Force Diagram underneath the beam. Finally calculating the moments can be done in the following steps: 2.

moment de force formule
Figure2:Acantileveredbeam. Free-body diagrams Asasimplestartingexample,considerabeamclamped(\cantilevered")atoneendandsub-jectedtoaloadPatthefreeendasshowninFig.2. Being able to draw shear force diagrams (SFD) and bending moment diagrams (BMD) is a critical skill for any student studying statics, mechanics of materials, or structural engineering. There is a long way and a quick way to do them. The long way is more comprehensive, and generates expressions for internal shear and internal bending moment in. Shear force and bending moment diagrams are powerful graphical methods that are used to analyze a beam under loading. This page will walk you through what shear forces and bending moments are, why they are useful, the procedure for drawing the diagrams and some other keys aspects as well. If you're not in the mood for reading, just watch the video! Shear and moment diagrams are graphs which show the internal shear and bending moment plotted along the length of the beam. They allow us to see where the maximum loads occur so that we can optimize the design to prevent failures and reduce the overall weight and cost of the structure. Since beams primarily support vertical loads the axial.

Elastic bending moment diagram (BMD) for 2span purlin system, together... Download Scientific
The bending moment diagram indicates the bending moment withstood by the beam section along the length of the beam. It is normal practice to produce a free body diagram with the shear diagram and the bending moment diagram position below For simply supported beams the reactions are generally simple forces. When the beam is built-in the free. Unloaded prismatic beam. Consider an unloaded prismatic beam fixed at end B, as shown in Figure 12.2. If a moment M1 is applied to the left end of the beam, the slope-deflection equations for both ends of the beam can be written as follows: M1 = 2EK(2θA) = 4EKθA (1.12.1) (1.12.1) M 1 = 2 E K ( 2 θ A) = 4 E K θ A.
A bending moment diagram provides a graphical representation of how bending moment changes along the length of a beam. In this diagram, the horizontal axis (x) typically represents the length of the beam and the vertical axis (y) represents the magnitude and direction of the bending moment. In solid mechanics, a bending moment is the reaction induced in a structural element when an external force or moment is applied to the element, causing the element to bend. [1] [2] The most common or simplest structural element subjected to bending moments is the beam.
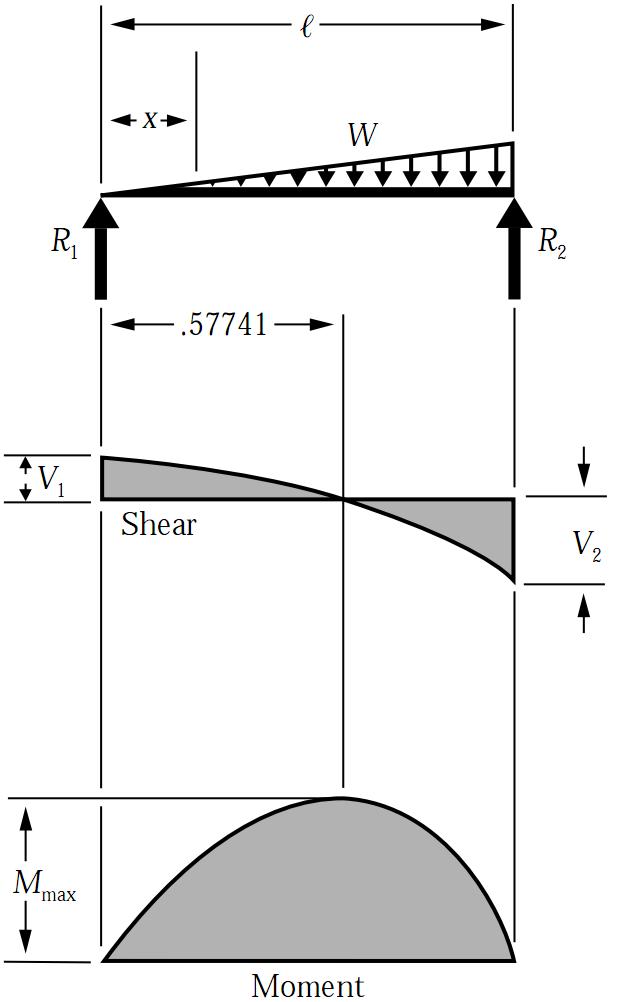
Simply Supported UDL Beam Formulas Bending Moment Equations
This section covers shear force and bending moment in beams, shear and moment diagrams, stresses in beams, and a table of common beam deflection formulas. Contents Constraints and Boundary Conditions Shear Force and Bending Moment Sign Convention Shear and Moment Diagrams Bending Stresses in Beams Shear Stresses in Beams The tables below give equations for the deflection, slope, shear, and moment along straight beams for different end conditions and loadings. You can find comprehensive tables in references such as Gere, Lindeburg, and Shigley. However, the tables below cover most of the common cases.



