Il cubo di un binomio è il prodotto notevole (A±B) 3 =A 3 ±3A 2 B+3AB 2 ±B 3 e si calcola come cubo del primo monomio, più o meno il triplo prodotto del primo monomio al quadrato per il secondo, più il triplo prodotto del primo monomio per il quadrato del secondo, più o meno il cubo del secondo monomio. Un binomio al cubo, es un polinomio de dos términos que se encuentra elevado a la potencia de 3, el cual indica el producto de tres binomios exactamente iguales. Es una expresión algebraica de la forma: (a ± b)3 Donde "a" y "b" son términos del binomio que pueden estar sumando o restando.

Producto notable tres cuatro cubo de un binomio
El cubo de un binomio o binomio al cubo, es una expresión algebraica, formada por dos términos que se pueden sumar o restar; y en la cual las operaciones de (suma o resta) estarán elevadas al cubo. Un binomio al cubo es un polinomio formado por dos términos elevado a la 3. Por lo tanto, la expresión algebraica de un binomio al cubo puedes ser (a+b)3 o (a-b)3, dependiendo de si se suman o se restan sus monomios. Además, el binomio elevado al cubo forma parte de las identidades notables (o productos notables). Anterior: https://youtu.be/eMazh3oiRgw Siguiente: https://youtu.be/HeUFsZX92e8Curso de Álgebra: https://www.youtube.com/playlist?list=PL9SnRnlzoyX1sF5fX83Cl. Es el volumen de un cubo cuyo lado es un binomio, es decir, matemáticamente hablando o . Este es un producto notable que se puede demostrar geometricamente como algebraicamente, de donde se obtiene la formula para resolver cual ejercicio de forma general. Demostración geométrica

BINOMIO AL CUBO YouTube
Explicación paso a paso de la forma de encontrar la solución del cubo de un binomio, dos ejercicios de aplicación dentro del curso de productos notables.Curs. Binomio de suma al cubo. Un binomio al cubo (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo. (a + b) 3 = a 3 + 3 · a 2 · b + 3 · a · b 2 + b 3 (x + 3) 3 = x 3 + 3 · x 2 · 3 + 3 · x· 3 2 + 3 3 = = x 3 + 9x 2 + 27x + 27 . Binomio de resta al cubo. Binomio al cubo , video donde explicamos la regla para elevar un binomio al cubo con ejemplos claros del mas simple al mas complejo. Más videos de álgebra en. Introducción al teorema binomial. Google Classroom. Acerca de. Transcripción. El teorema binomial nos dice cómo desarrollar expresiones de la forma (a+b)ⁿ, por ejemplo (x+y)⁷. Mientras mayor sea la potencia, es más difícil desarrollar expresiones como esta directamente. Pero con el teorema binomial ¡el proceso es relativamente rápido!
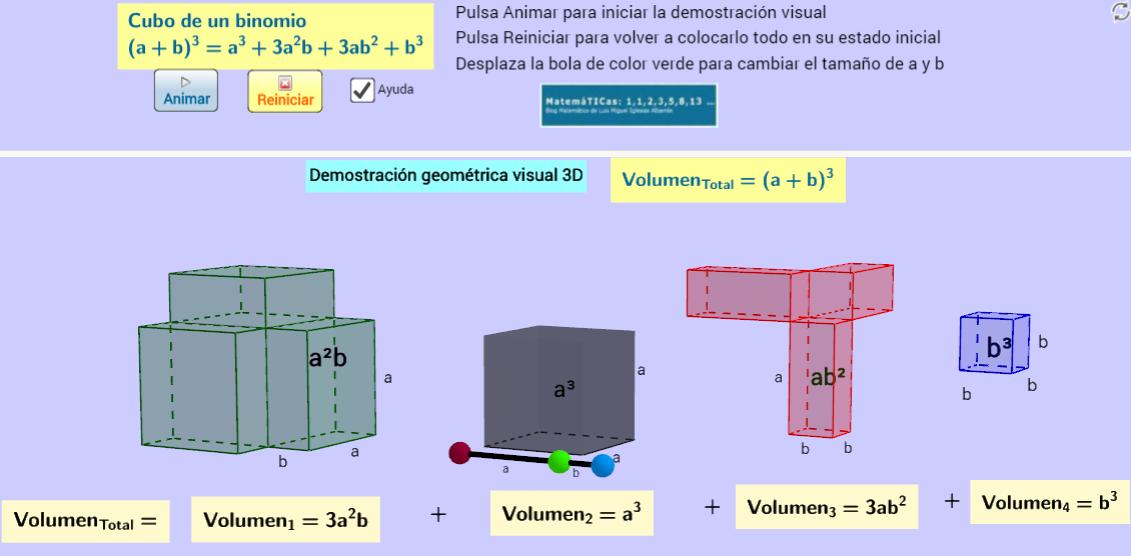
Demostración visual con Geogebra 3D. Desarrollo del cubo de un binomio
Los binomios al cubo, también conocido como cubo de un binomio, pertenece a los productos notables, de hecho es una de sus muchas identidades. Los productos notables contienen fórmulas que son de mucha importancia en el desarrollo y resolución de algunos procedimientos matemáticos. Suma de cubos: La suma de un binomio al cubo es igual al primer término al cubo, más tres veces el cuadrado del primer término por el segundo término, más tres veces el primer término por el cuadrado del segundo término, más el cubo del segundo término: { { (a+b)}^3}= { {a}^3}+3 { {a}^2}b+3a { {b}^2}+ { {b}^3} (a + b)3 = a3 + 3a2b + 3ab2 + b3
Cubo de un binomio. Las siguientes son las formas básicas de los cubos de binomio. Nuevamente encontramos un proceso repetitivo este se puede acortar así: El cubo de la suma de dos cantidades ( (a + b)3 ) es igual al cubo de la primera (a3) más el triple producto del cuadrado de la primera por la segunda (3a2b) más el triple producto de la. Primero notemos que el binomio al cubo podemos expresarlo como el producto de un binomio al cuadrado con el mismo binomio elevado a la primera potencia, entonces. Como ya vimos el Binomio al Cuadrado se desarrolla como , entonces. Observación: Notemos que cuando los términos del binomio van restando, podemos escribir la fórmula como sigue.

BINOMIO AL CUBO EJERCICIOS RESUELTOS pdf
Recuerda que elevar algo al cubo es multiplicar ese algo por sí mismo tres veces: Apliquemos propiedad distributiva entre los dos primeros binomios de la siguiente manera: Ahora tenemos un trinomio por un binomio: Aplicamos propiedad distributiva nuevamente: Operamos términos semejantes: Tu decides si aplicas el bello poema el primero al cubo. En esta ocasión hablaremos del binomio al cubo. Este producto notable es el producto del binomio por sí mismo, y otra vez: (a + b)* (a + b)* (a + b). Es lo mismo que elevar el binomio al exponente 3. Para obtener el resultado de esta operación algebraica, se sigue una regla ya establecida, que dice: Cubo del primer término: (a) 3 = a 3




