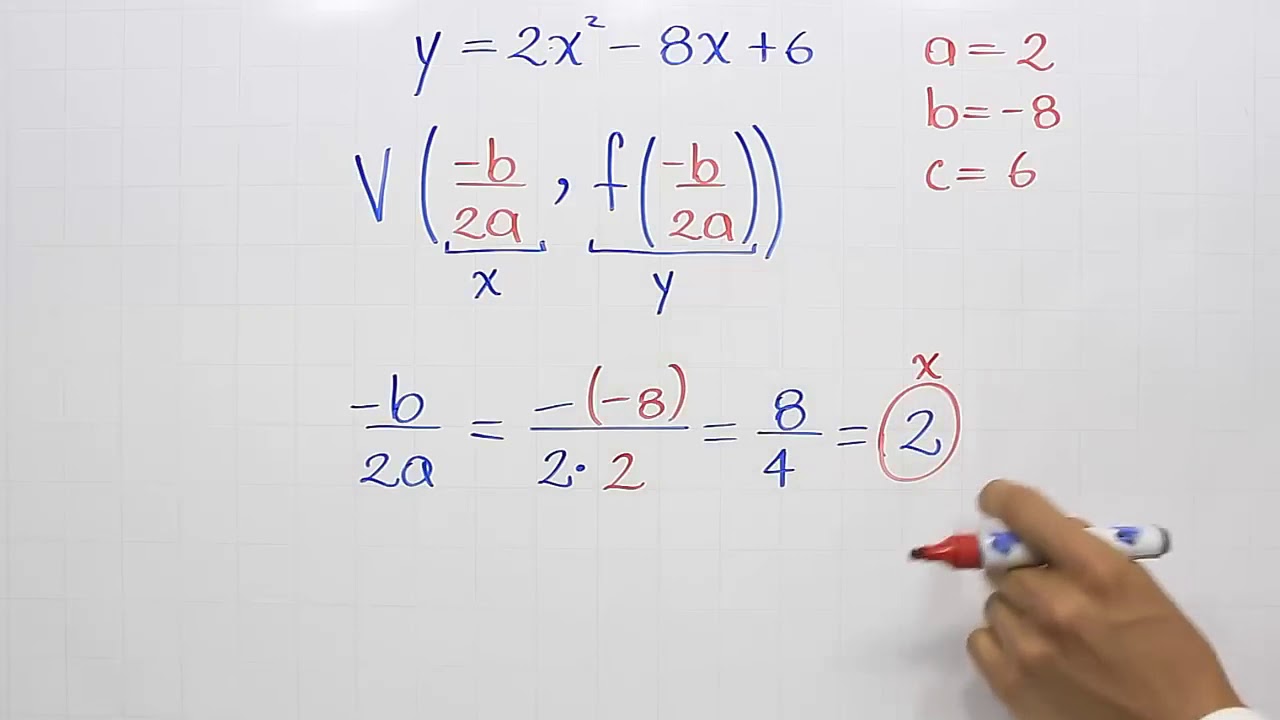Il vertice di una parabola è il punto di intersezione tra l' asse di simmetria e la parabola; le formule per il vertice permettono di determinarne le coordinate a partire dall'equazione della parabola, a seconda che essa sia ad asse di simmetria verticale od orizzontale. Il vertice è l'unico punto della parabola nel quale la retta tangente ha coefficiente angolare nullo ed è del tipo y=q, con q ordinata del vertice. Per parabole con asse di simmetria parallelo all'asse delle x, l'equazione di tale retta tangente sarà del tipo x=k.

Matematica Impariamo a calcolare il vertice della parabola YouTube
Calcolare il vertice di una parabola che ha per equazione y=x^2-2x+3. Come prima cosa: osserviamo l'equazione. Capiamo immediatamente che si tratta di una parabola con asse parallelo ad y , di conseguenza dobbiamo utilizzare la formula del vertice relativa a tale tipologia: Calcolatore gratuito del vertice della parabola - calcola il vertice della parabola data l'equazione passo dopo passo. Se conosci i parametri a, b e c dalla forma standard di una parabola, puoi trovare le coordinate del vertice h e k utilizzando le formule: h = -b/(2a); e; k = c - b²/(4a). In alternativa, puoi valutare il valore della parabola in corrispondenza dell'argomento h, cioè k = ah² + bh + c. Questo calcolatore calcola gratuitamente le coordinate del vertice e dell'asse della parabola, mostrando tutti i passaggi. Disegna inoltre il grafico della parabola stessa.
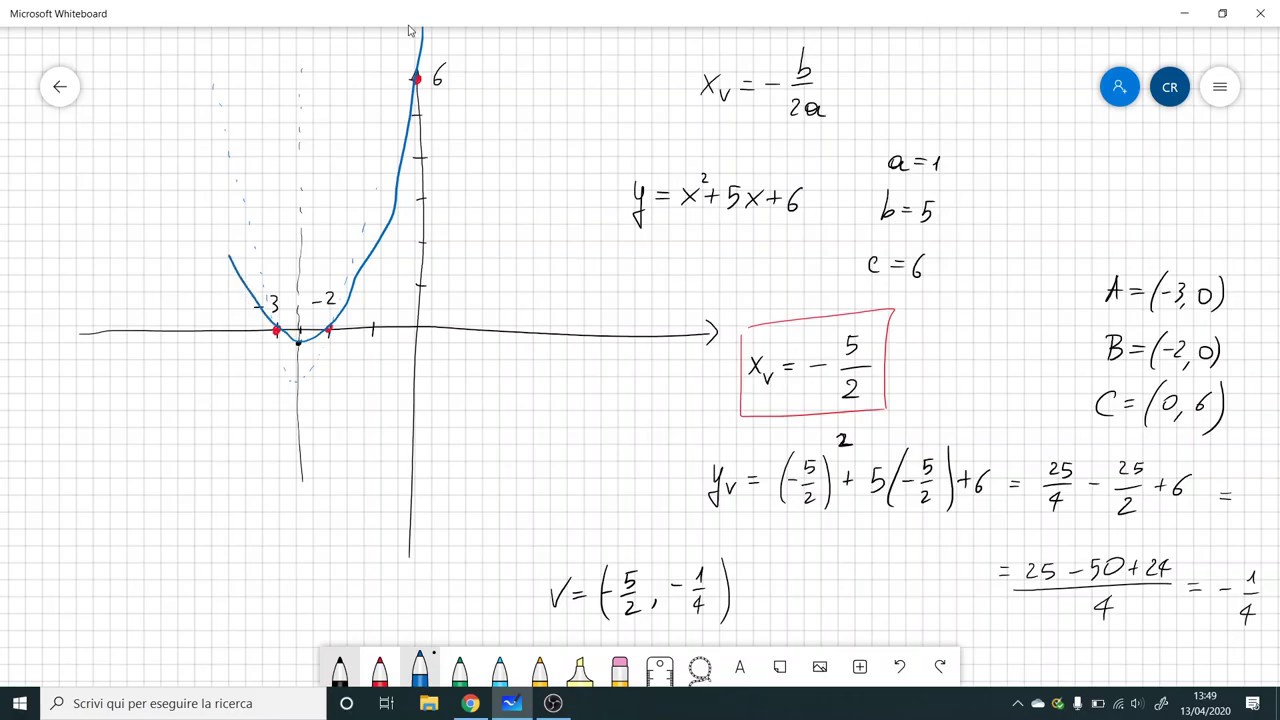
La parabola calcolo delle intersezioni con gli assi YouTube
Ecco come potrai trovare le coordinate del vertice di una parabola il cui l'asse è parallelo all'asse y. L'equazione generica della parabola, in questo caso, sarà: y = ax² + bx + c. La forma generale di un'equazione quadratica è y = ax² + bx + c. Puoi utilizzare questo calcolatore per la parabola per trasformare l'equazione nella forma del vertice, che ti permette di trovare i punti importanti della parabola — il vertice e il punto di fuoco. L'equazione della parabola nella sua forma del vertice è y = a (x - h)² + k. Nello specifico il calcolatore per risolvere la parabola online restituisce, tra le altre cose: - la rappresentazione grafica nel piano cartesiano; - le coordinate del vertice della parabola; - le coordinate del fuoco della parabola; - la direttrice della parabola; Problemi con la teoria e con le formule? La parabola è il luogo geometrico dei punti del piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice, e ha equazione y=ax 2 +bx+c se ha asse verticale oppure x=ay 2 +by+c se ha asse orizzontale. In termini più generali una parabola è una conica non degenere.
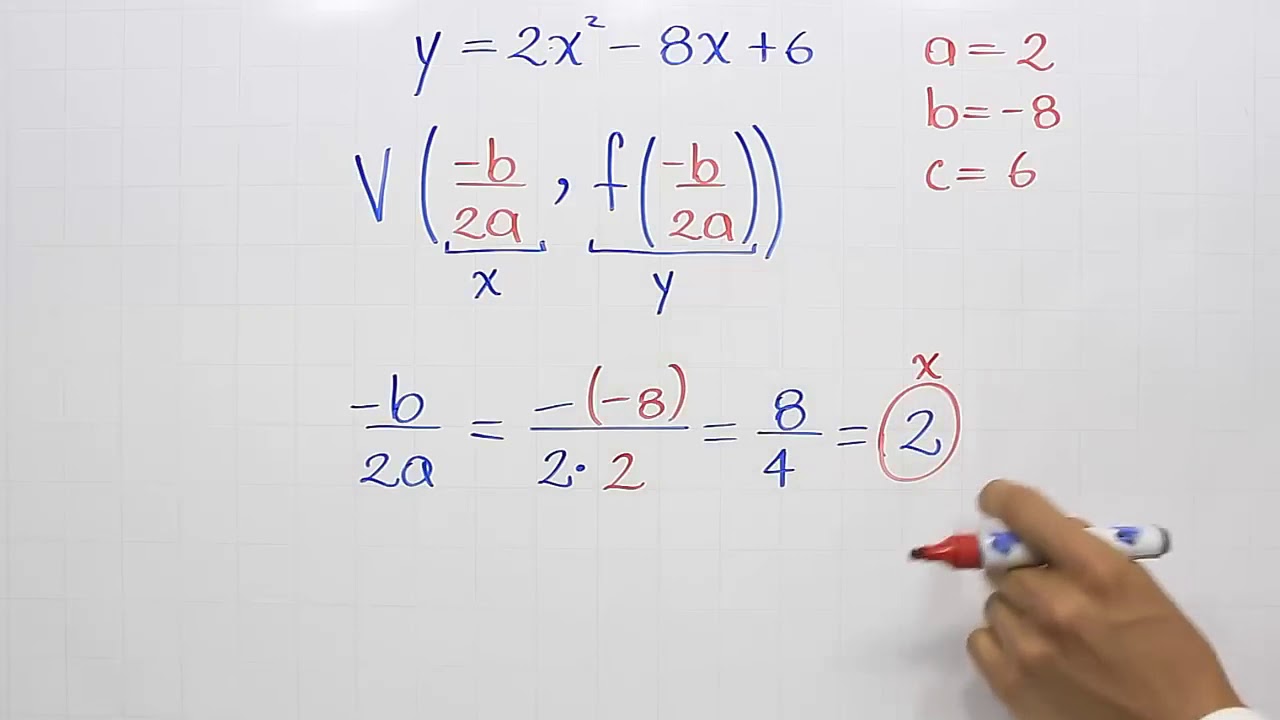
Vértice de una parábola YouTube
Per individuarli, esiste una determinata costruzione grafica. In particolare, dobbiamo rappresentare delle rette parallele ad {s} s, e considerare la distanza tra ciascuna retta tracciata e la retta {s} s. Tale distanza sarà, per ogni retta, l'apertura del compasso. Esercizio 1 Poiché a=1/2>0, la parabola presenta la concavità rivolta verso l'alto. L'equazione è del tipo y=ax² per cui il vertice della parabola coincide con l'origine degli assi e il suo asse di simmetria coincide con l'asse delle y. V= (0;0) Esercizio 2 y=-x²+4
Il vertice di una parabola con equazione quadratica del tipo ax^2 + bx + c si trova utilizzando la formula x = -b/ (2a) per l'ascissa del vertice, e poi calcolando l'ordinata Viene detto vertice della parabola il punto della parabola che ha ordinata minore o maggiore, a seconda che a >0 a > 0 o a<0 a < 0, rispettivamente. Conoscendo le coordinate (x_V, y_V) (xV ,yV ) del vertice V V, l'equazione della parabola si può riscrivere anche come: y-y_V = a (x-x_V)^2, \quad a \neq 0 y − yV = a(x− xV

Parabola trovare l'equazione della parabola passante per A e B con il
Il vertice Il vertice (V) è il punto in cui la parabola interseca l'asse. Nel vertice la parabola raggiunge il suo valore massimo o minimo a seconda del segno del coefficiente "a" dell'equazione della parabola y=ax 2 +bx+c. Le coordinate del vertice si posso calcolare nel modo seguente V ( − b 2a , − Δ 4a) V ( − b 2 a , − Δ 4 a) P \in \text {parabola} \Leftrightarrow d (P, F) = d (P, \text {direttrice}) P ∈ parabola ⇔ d(P,F) = d(P,direttrice) Scegliendo una direttrice parallela all'asse delle x x e un fuoco sull'asse y y, svolgendo i calcoli si trova l'equazione della parabola. y = a x^2 + b x + c y = ax2 + bx + c.