La funzione composta è una funzione che si ottiene mediante l'operazione di composizione di due funzioni. In sintesi la funzione composta si definisce applicando la seconda funzione alle immagini della prima. Funzioni composte Cos'è una funzione composta Una funzione è detta funzione composta quando il suo campo di definizione (dominio) coincide con l'immagine (codominio) di un'altra funzione. h(x) = f (g(x)) h ( x) = f ( g ( x)) Si legge f di g di x. Spesso la funzione composta è indicata anche con questa notazione h = f ∘ g h = f ∘ g
Funzione composta definizione, come calcolarla ed ESEMPI
In matematica, la composizione di funzioni è l'applicazione di una funzione al risultato di un'altra funzione. Funzioni composte Segui il nostro network: FUNZIONI COMPOSTE Per comprendere meglio questo argomento, leggi prima le seguenti lezioni: Funzioni reali di variabile reale Campo di esistenza delle funzioni Nozione di insieme Insiemi: alcuni simboli Sottoinsiemi propri e impropri Disegniamo tre insiemi: l'insieme X , il cui generico elemento è x; 1 Che cosa significa f o g ("f composta g") 2 L'insieme di definizione della funzione composta 3 Andamento di una funzione composta Che cosa significa f o g ("f composta g") Il simbolo "o" è il segno dell'operazione tra funzioni chiamata composizione. Funzioni composte: spiegazione ed esempi Date f f e g g la funzione composta f \circ g f ∘ g (che si legge, " f composto g") è quella che preso un valore della variabile x x, prima calcola g (x) g(x) e poi applica f f al valore g (x) g(x).

PPT FUNZIONE DEFINIZIONE PowerPoint Presentation, free download ID
Linea Definizione Magazine Arte Cataloghi funzione composta funzione composta funzione risultante dalla composizione di altre due funzioni. La funzione composta di due funzioni ƒ e g è la funzione ƒ ∘ g definita da ƒ (g (x)) (occorre porre attenzione al fatto che la scrittura ƒ ∘ g indica che opera prima la funzione g e poi la funzione ƒ ). Analisi Matematica 1 Derivate Il teorema per la derivata della funzione composta, detto anche teorema di derivazione della funzione composta o chain-rule, è una regola che permette di calcolare la derivata di una composizione di funzioni sotto forma di prodotti e derivazioni concatenate. 3. Costruire l'espressione analitica della funzione composta h g f e determinare il relativo insieme di definizione. Soluzione 1. Le funzioni f e h sono razionali intere ed hanno come dominio tutto l'asse reale. La funzione g è irrazionale intera ed è definita per i valori reali della variabile che rendono il Videolezione sulla composizione delle funzioni: spiegazione semplice su com'è definita la funzione composta, con esercizi svolti su come comporre due, o più.

Funzione composta (prodotto di funzioni) Altramatica
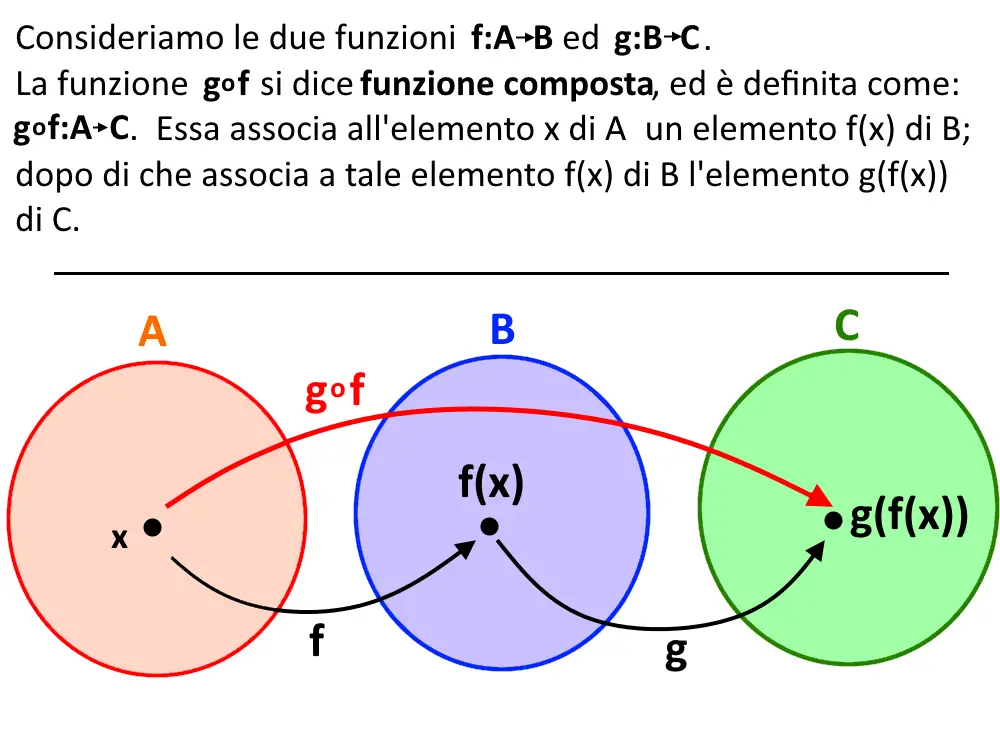
Funzione Composta Date due funzioni g: A→ B e f : B→ C si puo` definire la funzione composta: f g: A → C x→ g(x) → f (g(x)) notazione funzionale y= f (g(x)) La composizione ha senso se il valore g(x) appartiene al dominio della funzione f. Il dominio della funzione composta `e costituito dai soli valori di x per i quali la In questo video sarai guidato alla scoperta della composizione di funzioni. Imparerai la definizione di funzione composta e le proprietà che la caratterizzan.
Cosa significa tutto questo in breve? Ricordiamo che una funzione f:A \to B f: A → B è come una scatola: vi entra un "input", questo input passa nella scatola e viene trasformata in "output" dalla scatola stessa. Se x è l'input, l'output è f (x). Osservate come si mette l'input dentro la f ()! Una funzione composta invece passa per due scatole! Ciao! Nel #math di oggi, continuiamo a parlare di funzioni, imparando cosa si intende per funzione composta e come si effettua la composizione di due funzion.

Funzione composta definizione, come calcolarla ed ESEMPI
Quindi, attraverso la funzione composta ∘ Ad corrisponde ; → In altre parole, una funzione è composta laddove si "sovrappongono" due o più funzioni Esempio: È una funzione composta in quanto all'interno della radice non compare una semplice variabile indipendente (la ), ma un'altra funzione (in questo caso una funzione razionale. Esempi illustrativi di funzioni e funzioni composte. Vediamo, con alcuni esempi di funzioni, che: Una funzione può avere valori diversi per diversi intervalli di dominio; Una funzione f (x) f (x) può essere funzione tanto di una x x che di una g (x) g(x), ossia possono comparire nella sua espressione tanto la variabile indipendente




