De Broglie hypothesis Propagation of de Broglie waves in one dimension - real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the color opacity) of finding the particle at a given point x is spread out like a waveform; there is no definite position of the particle. de Broglie Wave Equation. Planck's investigation of the emission spectra of hot objects and the subsequent studies into the photoelectric effect had proven that light was capable of behaving both as a wave and as a particle. It seemed reasonable to wonder if electrons could also have a dual wave-particle nature. In 1924, French scientist Louis.
De Broglie theory (Duality) Overall Science
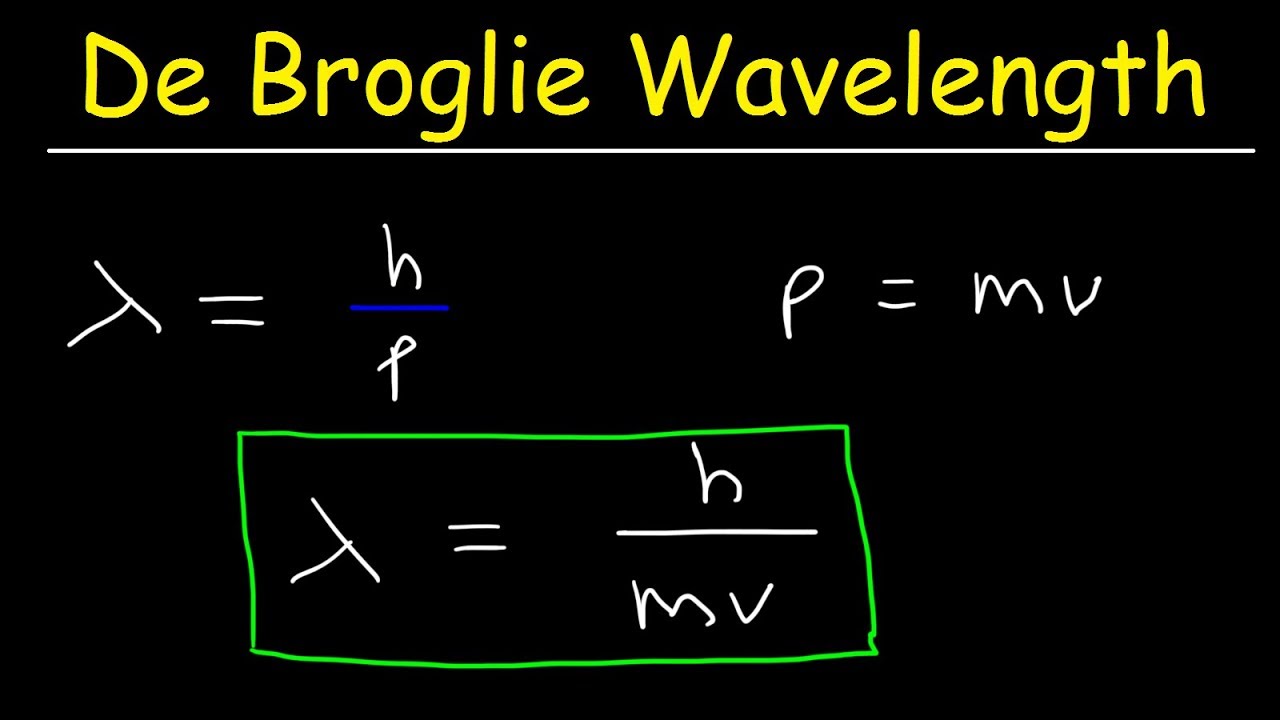
De Broglie was able to mathematically determine what the wavelength of an electron should be by connecting Albert Einstein's mass-energy equivalency equation (E = mc 2) with Planck's equation (E = hf), the wave speed equation (v = λf ) and momentum in a series of substitutions. The de Broglie equation is an equation used to describe the wave properties of matter, specifically, the wave nature of the electron : λ = h/mv, where λ is wavelength, h is Planck's constant, m is the mass of a particle, moving at a velocity v. de Broglie suggested that particles can exhibit properties of waves. The de Broglie wavelength of the photon can be computed using the formula: λ = h p = 6.63×10−34 1.50×10−27 = 4.42 ×10−7 = 442 ×10−9 = 442 Nano meter. Therefore, the de Broglie wavelength of the photon will be 442 nm. This wavelength will be in the blue-violet part of the visible light spectrum. Is it a particle or a wave? This is the question that physicists of the 1920s were asking about light. In 1924, Louis de Broglie took this question to another level as he explored how electrons - which are matter, and were thought to be simply particles - can behave like waves. Questions Tips & Thanks Sort by: Top Voted Patrick 7 years ago

De Broglie Wavelength Formula Equation, Concept, Solved Examples
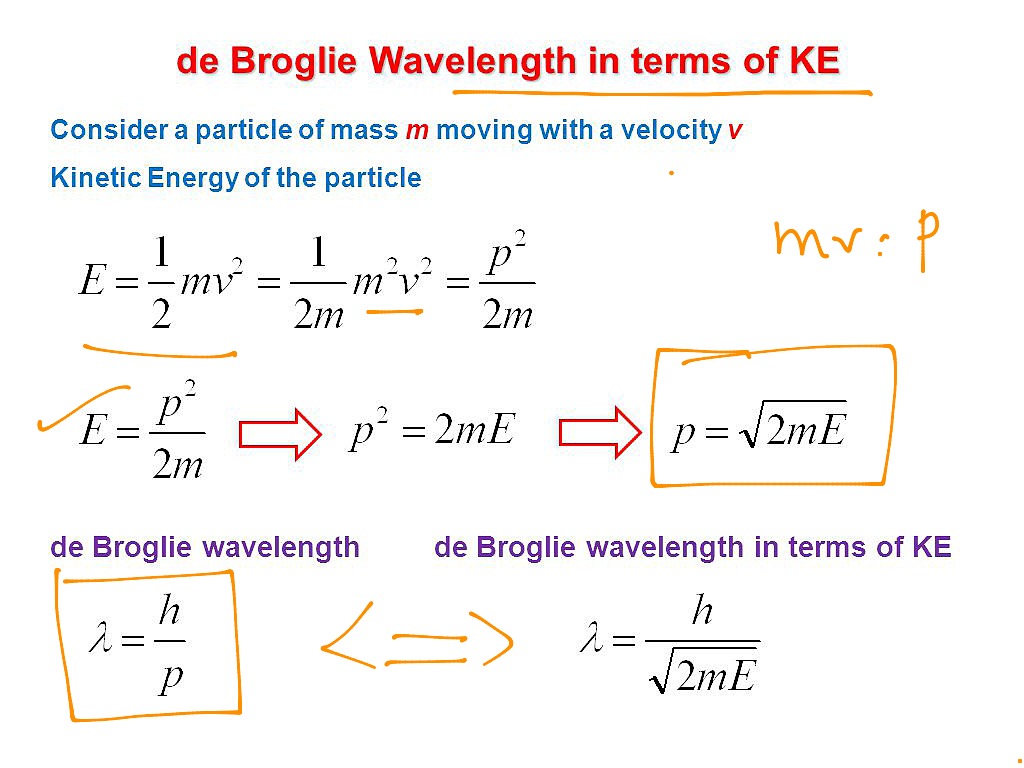
Derivation de Broglie derived the above relationship as follows: 1) E = hν for a photon and λν = c for an electromagnetic wave. 2) E = mc 2, means λ = h/mc, which is equivalent to λ = h/p. Note: m is the relativistic mass and not the rest mass since the rest mass of a photon is zero. Compton's formula established that an electromagnetic wave can behave like a particle of light when interacting with matter. In 1924, Louis de Broglie proposed a new speculative hypothesis that electrons and other particles of matter can behave like waves. Today, this idea is known as de Broglie's hypothesis of matter waves.In 1926, De Broglie's hypothesis, together with Bohr's early. Through the equation λ λ, de Broglie substituted v/λ v / λ for ν ν and arrived at the final expression that relates wavelength and particle with speed. mv2 = hv λ (5) (5) m v 2 = h v λ. Hence. λ = hv mv2 = h mv (6) (6) λ = h v m v 2 = h m v. A majority of Wave-Particle Duality problems are simple plug and chug via Equation 6 6 with. Solution: Reasoning: The de Broglie wavelength of an object is defined as λ = h/p. Details of the calculation: λ = h/p, E = p 2 / (2m), p = √ (2mE), λ = h/√ (2mE). The energy of the electron is 25000 eV * 1.6*10 -19 J/eV = 4*10 -15 J. λ = (6.626*10 -34 Js)/√ (2*9.1*10 -31 kg*4*10 -15 J) = 7.8*10 -12 m.
de Broglie equation Science, quantum theory ShowMe
To determine the de Broglie wavelength of a particle given its mass and velocity, you need to: Multiply the velocity by mass. Their product is the particle's momentum. Divide Planck's constant by the momentum found in Step 1. The result you've got is exactly the de Broglie wavelength of your particle. Congrats! This chemistry video tutorial explains how to calculate the de broglie wavelength of large objects and small particles such as electrons. It contains plenty.
Now comes the second equation. It is one of two related equations called the de Broglie equations. You can read more about de Broglie's work here. He received the 1929 Nobel Prize in Physics for this work. (I will discuss the second de Broglie equation below the following example problems.) Equation Number Two: λ = h/p In 1924, French scientist Louis de Broglie derived an equation, known as the De Broglie Wavelength Formula, that described the wave nature of any particle. Thus, establishing the wave-particle duality for the matter. Microscopic particle-like electrons also proved to possess this dual nature property.

What is the significance of de Broglie's equation? Quora
De Broglie's hypothesis is an independent postulate about the structure of nature. In this respect, its status is the same as that of Newton's laws or the laws of thermodynamics. Nonetheless, we can construct a line of thought that is probably similar to de Broglie's, recognizing that these are heuristic arguments and not logical. De Broglie Wavelength Formula is used to calculate the wavelength and momentum in any given problems based on this concept. Solved Examples Question 1: Find the wavelength of an electron moving with a speed of ms-1. Solution: Given: Velocity of the electron, v =2 ×106 ms-1 Mass of electron, m =9.1 ×10-31 Kg



