Formule dei poligoni regolari. Prima di elencare le formule dei poligoni regolari dobbiamo specificare un po' di simboli.Chiameremo N il numero di lati, L la lunghezza del lato, a l'apotema (raggio circonferenza inscritta), f il numero fisso, φ la costante d'area, R il raggio della circonferenza circoscritta, 2p il perimetro, p il semiperimetro e A l'area del poligono regolare. L'area di un poligono è rappresentata dalla superficie interna del poligono, cioè la porzione di piano racchiusa all'interno dei lati del poligono. In questo articolo troverai tutte le formule per calcolare l'area dei poligoni: dall'area del rettangolo a quella del parallelogramma e del quadrato, insieme anche ad una tabella riassuntiva che ti aiuterà soprattutto durante la fase del.
MATEMATICA, SCIENZE, EDUCAZIONE Aree di poligoni
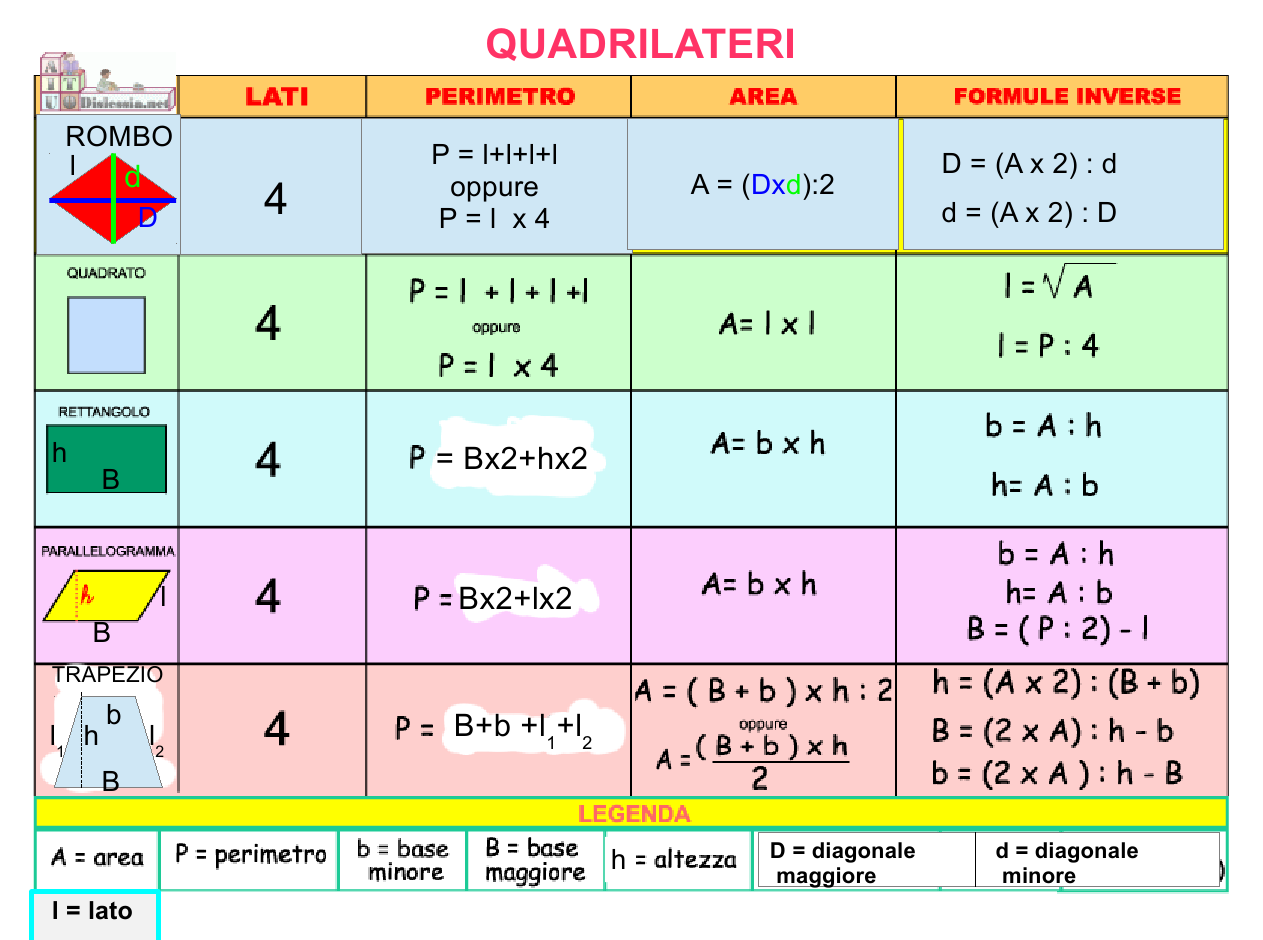
Area di un poligono regolare conoscendo il lato. Area di un poligono circoscritto. Ricapitoliamo in una tabella le FORMULE delle AREE delle FIGURE PIANE viste nelle lezioni precedenti e le relative FORMULE INVERSE. FIGURA GEOMETRICA. FORMULA DIRETTA. FORMULE INVERSE. Rettangolo. A = b x h. b = A/ h. Definizione e classificazione dei poligoni. Definizione di poligono. Si definisce poligono una qualsiasi figura geometrica delimitata da una linea spezzata chiusa, in cui i segmenti che la costituiscono vengono detti lati e i punti di incontro dei lati vengono chiamati vertici.La prima e più generale classificazione prevede di distinguere tra poligoni semplici e poligoni complessi. Formule dell'area dei poligoni. Nella tabella sottostante elenchiamo le formule dirette che si usano per calcolare le aree dei poligoni che si studiano in Geometria Piana. Cliccando sul nome di ciascun poligono è possibile consultare un intero formulario dedicato alla figura scelta, in cui proponiamo tutte le formule, comprese le formule. Definizione. Si dice apotema di un poligono regolare il raggio del cerchio inscritto nel poligono. In generale in un poligono regolare con n lati di lato l e apotema a: 2 p = n ⋅ l. A = p ⋅ a , semiperimetro per apotema.

Sussidiario delle Discipline 5
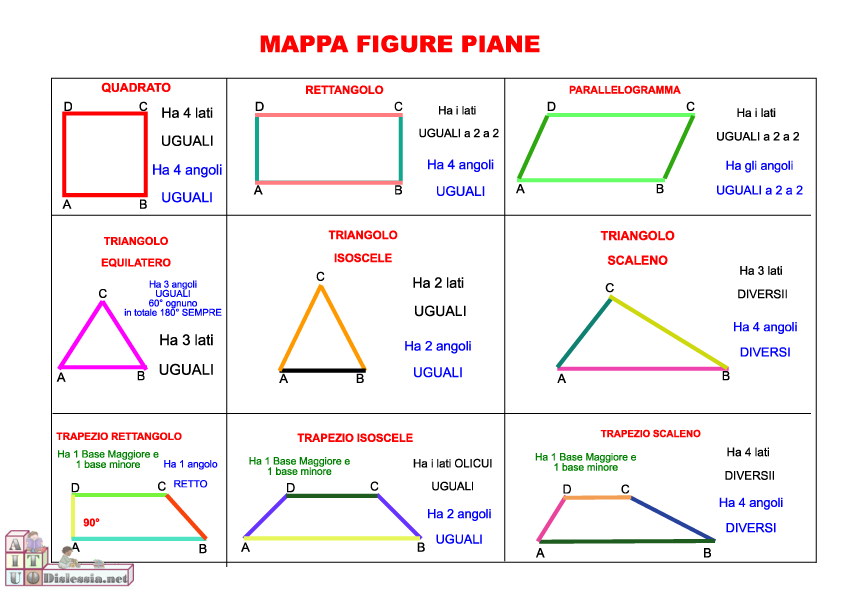
Cosa sono i poligoni. Ovviamente per spiegare cosa sono i poligoni non partiremo con le definizioni nude e crude. Invitiamo gli alunni a guardarsi intorno un momento e a fare attenzione agli oggetti che li circondano: il soffitto di una stanza, il pavimento e le piastrelle che lo costituiscono sono esempi concreti di ciò di cui parleremo tra poco: i poligoni. Formule per un poligono regolare. Esistono molte formule che si possono applicare a un qualsiasi poligono regolare di n n lati per ricavare alcune grandezze a esso relative. Se il lato del poligono misura l l, abbiamo: Perimetro: 2p = n \cdot l 2p = n ⋅l. Area: abbiamo a disposizione alcune formule, a seconda di cosa conosciamo; per esempio: In realtà i poligoni regolari non finiscono qua: esistono infatti l'ettagono (con 7 lati), l'ottagono (con 8 lati), l'ennagono (con 9 lati), il decagono (con 10 lati) e così via. Caratteristiche dei poligono regolari Poligoni. Un poligono è una figura piana chiusa i cui lati sono dei segmenti. Un poligono può avere un numero arbitrario di lati e angoli, ma i lati non possono essere curvi. Quale delle seguenti figure è un poligono? Per vedere più contenuti, devi prima completare tutte le attività e gli esercizi precedenti.

Paradiso delle mappe Perimetro e area poligoni 1
Passiamo ora alla classificazione dei poligoni. Essi possono essere divisi in base al numero di lati o in base al numero di angoli. triangolo: tre lati e tre angoli; quadrilatero: quattro lati e quattro angoli (se i lati sono uguali si tratta di un quadrato); pentagono: cinque lati e cinque angoli; esagono: sei lati e sei angoli; Definizione e caratteristiche dei vari poligoni, con esempi e immagini per distinguerli.. Figure piane: formule e come riconoscerle; Tipi di angolo: caratteristiche e descrizione;
L'area di un poligono è la misura della superficie interna del poligono, ovvero la misura della porzione di piano racchiusa tra i lati del poligono. Vediamo alcune formule utili per calcolare l'area dei poligoni: Rettangolo A s = a·b. Dove: a=lato 1. b=lato 2. Quadrato A s = a 2. Dove: I POLIGONI In questa lezione ci occuperemo delle FIGURE GEOMETRICHE PIANE. Con questa espressione si intende UN QUALSIASI INSIEME DI PUNTI APPARTENENTI AD UNO STESSO PIANO. Disegniamo il PIANO α: Ricordiamo α è una lettera dell'alfabeto greco e si legge Alfa.
Coach Brita Poligoni e non poligoni
Calcolare l'area dei poligoni utilizzando altre formule, ad esempio per un triangolo scaleno o un quadrilatero. Come si usa il calcolatore per l'area del poligono regolare — un esempio Supponiamo che tu voglia calcolare l'area di uno specifico poligono regolare, ad esempio un poligono con 12 lati o un dodecagono con lati di 5 centimetri. Inserisca il numero dei lati. il numero dei lati. n = Inserisca 1 valore. lato. a = cerchio circoscritto (raggio) R = cerchio inscritto (raggio). Arrotondare a cifra decimale. Il procedimento di calcolo. Formule poligono. n: il numero dei lati: area $$ A = \frac{1}{4} n a^2 \cot\frac{180^\circ}{n} $$ perimetro $$ P = n \cdot a $$




