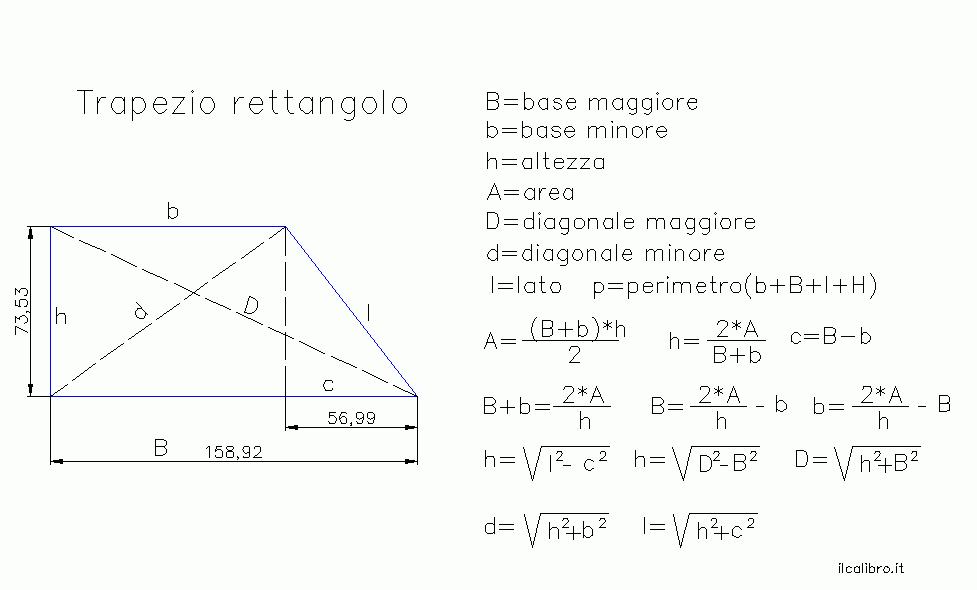B + b = 2p - 2 × L. Formule del Trapezio rettangolo: area, perimetro, base maggiore, base minore, altezza. Disegno, definizione e proprietà. Formule del trapezio Ora occupiamoci delle formule del trapezio. Partendo dal caso generale passiamo successivamente alle formule del trapezio rettangolo e alle formule del trapezio isoscele, casi in cui le formule generali per area e perimetro continuano ovviamente a valere.
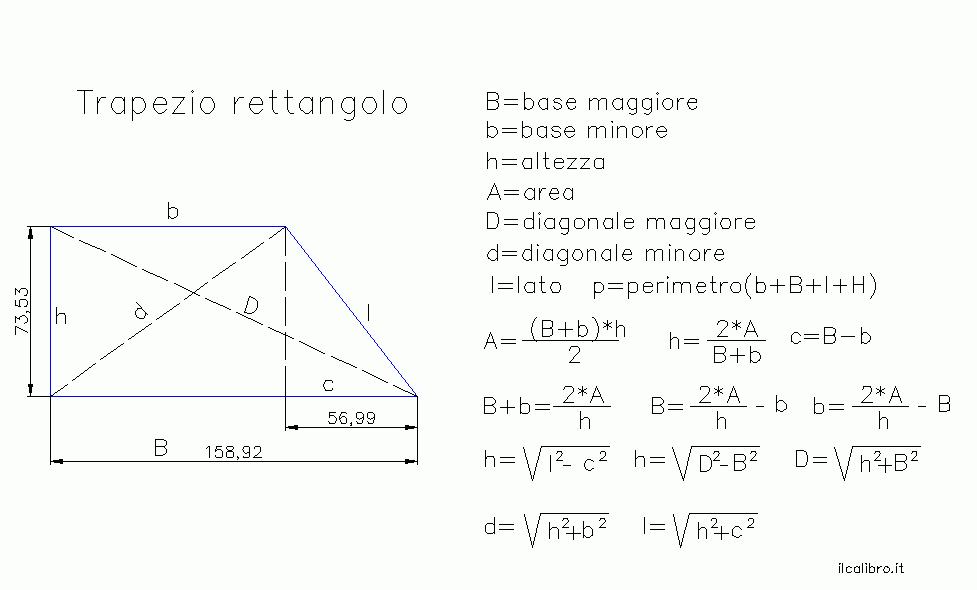
GEOMETRIA PIANA Formule del Trapezio
Il perimetro del trapezio rettangolo si ottiene sommando le due basi (maggiore e minore) e i due lati del trapezio. Formula del perimetro del trapezio isoscele: P = B + b + L1 + L2 Il trapezio rettangolo è chiamato così perché possiede un angolo interno di 90°. Formule Trapezio Rettangolo Dirette e Inverse A= area, b= base minore, B= base maggiore, l= lato obliquo, h= altezza o altro lato, HB= spazietto sulla base maggiore, d= diagonale minore, D= diagonale maggiore. Area = [(b+B) * h] / 2 Altezza = 2A / (b + B) HB. Cominciamo con le formule dirette: perimetro = base minore+base maggiore+altezza+lato obliquo area = [ (base minore+base maggiore) x altezza] : 2 Procediamo, ora, con le formule inverse che possono esserti molto utili in diversi casi. Per alcune sarà necessario applicare anche il Teorema di Pitagora: Gli angoli Un TRAPEZIO si dice RETTANGOLO se: i LATI OBLIQUI sono DISUGUALI; uno dei lati obliqui è PERPENDICOLARE alle BASI. Disegniamo un TRAPEZIO RETTANGOLO: LA LEZIONE PROSEGUE SOTTO LA PUBBLICITA' Notiamo che i lati obliqui AD e BC sono disuguali. Inoltre il lato AD è perpendicolare alle basi AB e DC.
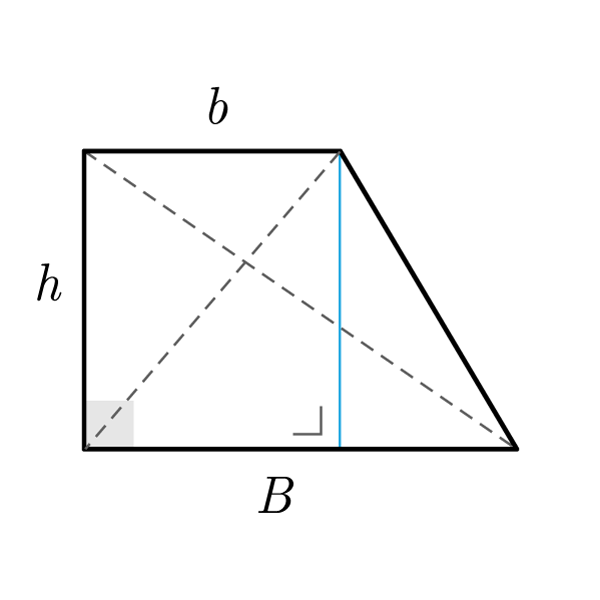
Formule Trapezio rettangolo Risolvi Geometria
Quali sono le formule del trapezio rettangolo? Come si calcolano perimetro e area? Scopriamolo insieme. Cominciamo dando una definizione precisa di trapezio. Si tratta di un quadrilatero che ha due lati paralleli detti basi e due lati obliqui. La formula dell'area del trapezio deriva da una equivalenza di superfici. Un trapezio è equivalente, infatti, ad un triangolo che ha la stessa altezza H del trapezio e per base b la somma delle. Il trapezio rettangolo è un trapezio per il quale i due angoli adiacenti ad un lato obliquo sono angoli congruenti e quindi retti. La figura del trapezio rettangolo è la seguente: Proprietà del trapezio isoscele L'area di un trapezio rettangolo è uguale a quella di qualsiasi altro trapezio. E' uguale al semiprodotto tra la somma delle basi (b 1 +b 2) per l'altezza (h). A = (b1 +b2)⋅h 2 A = ( b 1 + b 2) ⋅ h 2 Dove b 1 è la base minore, b 2 è la base maggiore e h è l'altezza del trapezio.

Teorema di Pitagora nel trapezio rettangolo YouTube
Formula per l'area del trapezio rettangolo L'area di un trapezio rettangolo si calcola come prodotto tra l'altezza e la somma delle basi, tutto fratto 2. A = ( (b+B)×h)/ (2) Nella formula A indica l'area, B la base maggiore, b la base minore e h l'altezza, che coincide con uno dei lati del trapezio. se uno dei due lati del trapezio è perpendicolare a una base (e quindi anche all'altra) il trapezio si dice trapezio rettangolo; se il trapezio non ha particolari proprietà, diremo che è un trapezio scaleno. Valgono i seguenti risultati: TEOREMA: Un trapezio è isoscele se e solo se gli angoli adiacenti a ciascuna base sono congruenti.
A seconda delle relazioni che sussistono tra i lati, si possono distinguere 3 tipi di trapezi: trapezio isoscele - quando i lati obliqui sono tra loro uguali. trapezio rettangolo - quando uno dei lati obliqui è perpendicolare alle basi. trapezio scaleno - quando i quattro lati sono diversi. Come si calcola l'area del trapezio rettangolo, isoscele e scaleno. Formule rapide, formule inverse dal perimetro del trapezio
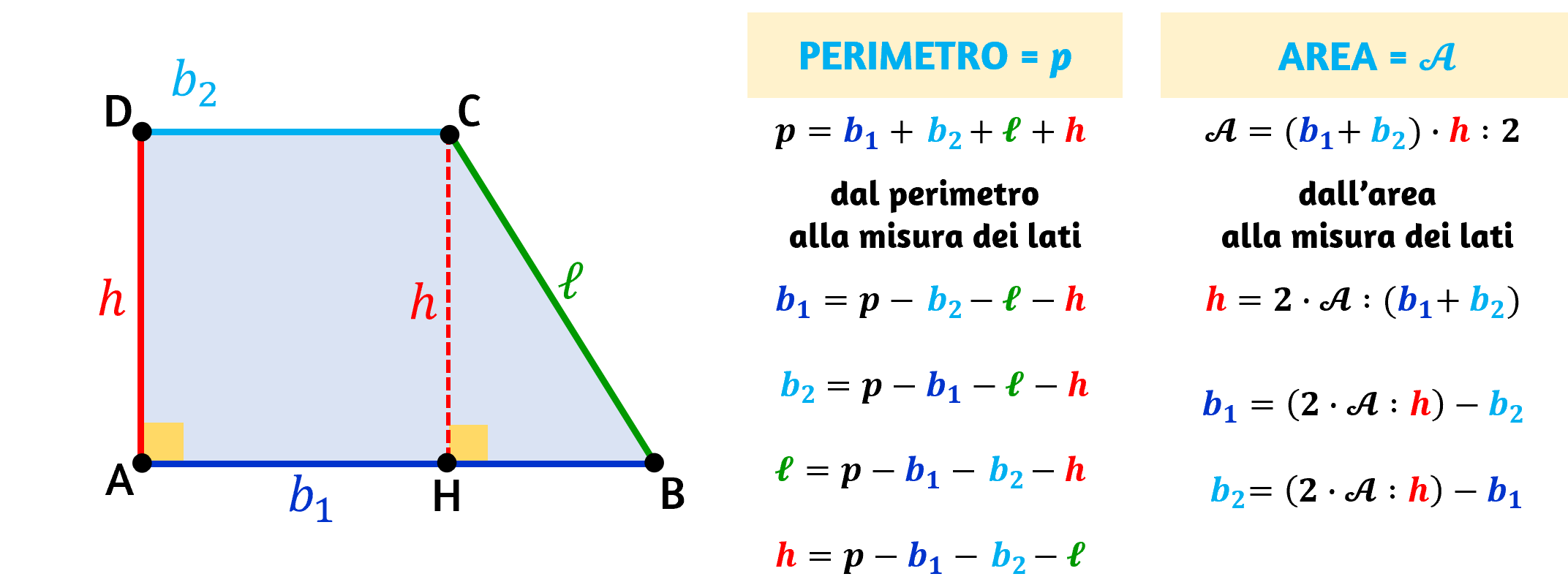
Come Si Trova L Altezza Del Trapezio Rettangolo bayiggins
Le formule del trapezio Tipi di trapezio Osservazioni Le formule del trapezio Le principali formule per calcolare le misure di un trapezio Perimetro Il perimetro del trapezio è uguale alla somma dei lati obliqui e delle basi. P = l1 + l2 +b1 + b2 P = l 1 + l 2 + b 1 + b 2 Area del trapezio Formule del Trapezio. Si chiama trapezio ogni quadrilatero con due soli lati opposti paralleli. I lati paralleli AB e CD si dicono basi e precisamente: AB è la base maggiore, CD la base minore. I lati non paralleli AD e BC si dicono lati obliqui o, semplicemente, lati.