Funzione crescente e funzione decrescente in termini rigorosi. In termini matematici si dice che una funzione è monotona se presenta sempre lo stesso andamento: cresce o decresce, e non l'una e l'altra cosa insieme.Se invece cresce su una porzione del dominio e decresce altrove, diciamo che la funzione considerata non è monotona.In sostanza una funzione è monotona se ha sempre lo stesso. Per verificare se una funzione è crescente o decrescente, si può usare il criterio di monotonia delle funzioni in base al quale c'è una relazione tra la derivata prima della funzione f(x) e la crescenza o decrescenza della funzione stessa. Funzione crescente. Una funzione f(x) continua in [a,b] e derivabile in (a,b) è crescente in [a,b] se.
06. Funzione crescente e decrescente
Esempi di funzioni crescenti e decrescenti. Consideriamo la seguente funzione f (x) = x f (x) = x. Consideriamo ad esempio l'intervallo I, cioè la parte destra del dominio D. Questa è sicuramente crescente in senso stretto, perché oltre a salire, non è mai costante. Ossia sale sempre in tutto I. Chiaramente lo è anche in tutto D. PROPOSIZIONE. Supponiamo che una funzione f f sia definita e continua su un intervallo I \subset \mathbb {R} I ⊂ R e derivabile in ogni punto interno di I I: allora dove la derivata è positiva la funzione è crescente, mentre dove è negativa, la funzione è decrescente. In simboli: f' (x) > 0 \ \forall x \in I \Rightarrow f '(x) > 0 ∀. Funzioni. La monotonia di una funzione è una proprietà che riguarda l'andamento di crescita e decrescita della funzione, e che può essere riferita al suo dominio o ad un intervallo contenuto in esso. Nella lezione precedente abbiamo presentato la nozione di monotonia in generale e la definizione di funzione crescente o decrescente. Funzione crescente e decrescente; Rapporto incrementale; Derivata prima; FUNZIONE CRESCENTE . Data una funzione ad una variabile reale diciamo che essa è crescente in un certo tratto se per qualsiasi coppia di punti x1 e x2 con x1 minore di x2 allora il valore della funzione in x2, ovvero f(x2) è maggiore o uguale al valore della funzione in.

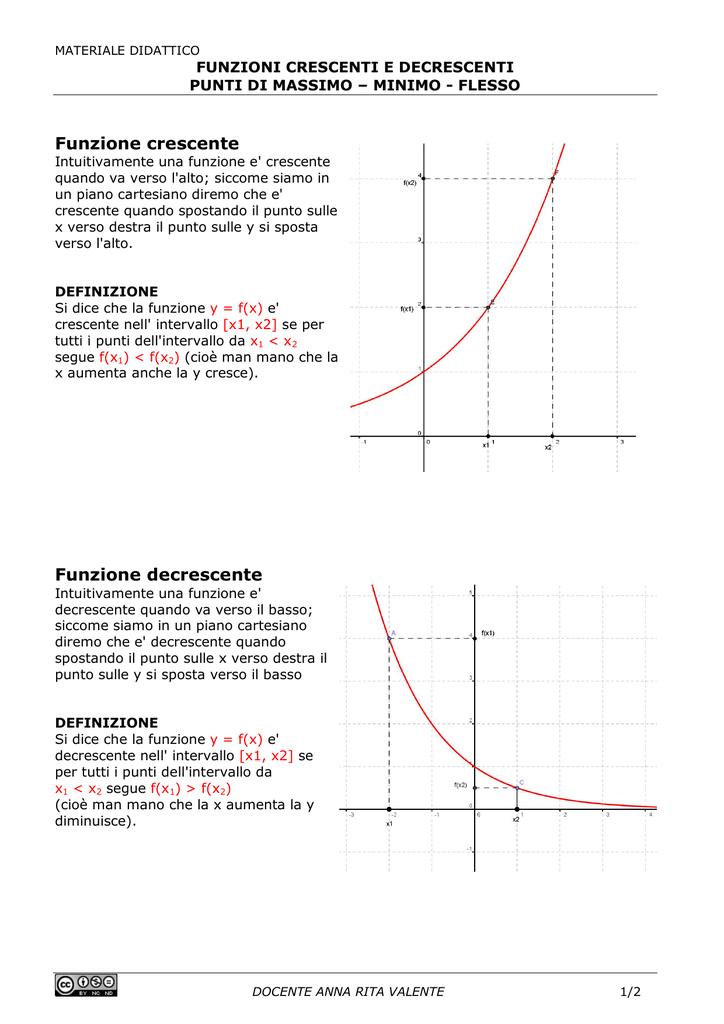
Funzione crescente e decrescente Funzione crescente Intuitivamente
Una funzione strettamente crescente è anche detta crescente in modo stretto. Le funzioni crescenti e strettamente crescenti appartengono all'insieme delle funzioni monotòne. Nota. Una funzione è detta monotòna in un intervallo del suo dominio se nell'intervallo è sempre crescente o sempre decrescente. Esempio. Considero la funzione $$ y=x^2 $$ Una funzione strettamente decrescente è anche detta decrescente in modo stretto. Le funzioni decrescenti e strettamente decrescenti appartengono all'insieme delle funzioni monotòne. Nota. Una funzione si dice monotòna in un intervallo quando è sempre crescente oppure decrescente nell'intervallo. Esempio. Considero la funzione $$ y=x^2 $$ IV) Esercizio calcolo e studio del segno della derivata prima di una funzione fratta con logaritmo. V) e VI) Due esercizi sullo studio di crescita e decrescita con le derivate. VII) Monotonia di una funzione fratta con radice a denominatore. VIII) Studiare crescita e decrescita di una funzione con differenza di esponenziali. Funzioni crescenti e decrescenti. Data una funzione , se si ha allora esiste un intorno di in cui la funzione è crescente. Se la derivata è positiva in tutti i punti di un intervallo, allora la funzione è crescente nell'intervallo. Analogo ragionamento si può fare per le funzioni decrescenti. Queste affermazioni si possono ricavare.

Monotonia e segno della derivata prima
E, in questo intervallo, quindi, la funzione è crescente. Di conseguenza, essendo la derivata della funzione negativa per ( x lt -1 \text{ e } x lt 1 ), in tali intervalli la funzione è decrescente. Un esempio di funzione decrescente è la funzione f(x) = -x. La funzione f(x) = x 2 risulta crescente nell'intervallo [0, + ∞), decrescente invece in (- ∞, 0). Graficamente ci aspettiamo che una funzione sia crescente se i valori sulle y diventano sempre maggiori guardando la funzione da sinistra a destra, decrescente invece se i valori delle y diventano sempre minori.
Crescenza e decrescenza. definizione di funzione crescente. definizione di funzione decrescente. legame fra la crescenza/decrescenza e derivata prima. funzione decrescente funzione decrescente funzione di una variabile, definita in un insieme ordinato E a valori in un insieme ordinato F, tale che per ogni coppia di punti x′ e x″ di E, con x′ < x″, ƒ(x′ ) ≥ ƒ(x″ ). Si definisce funzione decrescente nel punto x0 ∈ E una ƒ(x) tale che, presi comunque x′ e x″ ∈ E, con x′ < x0 < x″, si ha: ƒ(x′ ) ≥ ƒ(x0.

PPT FUNZIONE DEFINIZIONE PowerPoint Presentation, free download ID
Appunto di matematica per le scuole superiori che descrive che cosa sia la Funzione crescente, decrescente e punti stazionari, con analisi delle loro caratteristiche. Funzioni crescenti e decrescenti. Una funzione f (x) è monotona in un intervallo I se, per ogni x 1, x 2 ∈ I, risulta verificata una delle relazioni seguenti: f (x) decrescente : x1 < x2 ⇒ f (x1) ≥ f (x2). Si dice che f (x) è strettamente monotona in I, se essa è strettamente crescente, oppure se è strettamente decrescente in I.




