Home Lezioni Geometria Geometria Analitica L' iperbole in Geometria Analitica è il luogo geometrico dei punti del piano per cui è costante la differenza delle distanze da due punti fissi detti fuochi, ed è una conica. L' iperbole equilatera riferita ai propri asintoti è un'iperbole con gli asintoti perpendicolari coincidenti con gli assi. Si chiama iperbole il luogo geometrico dei punti del piano per i quali la differenza delle distanze da due punti fissi detti fuochi si mantiene costante in valore assoluto. Se poniamo uguale a 2a 2a il valore della costante, la definizione si traduce nella scrittura che segue: | \bar {PF_1} - \bar {PF_2} | = 2a ∣P F 1 − P F 2∣ = 2a

Iperbole equilatera riferita agli asintoti. Esercizio 412
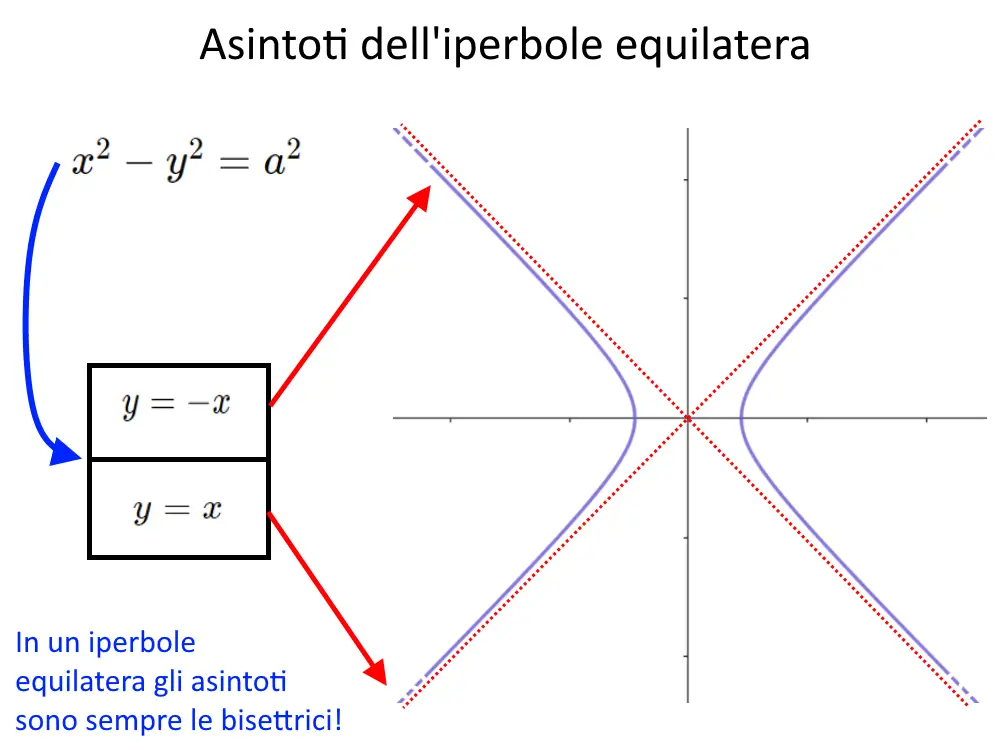
Soluzione L' equazione dell'iperbole equilatera genera solitamente molti dubbi perché può presentarsi in due diverse forme: riferita agli assi (detta anche in forma canonica) oppure riferita agli asintoti. Vediamo di fare chiarezza partendo dalla definizione di iperbole equilatera: è un'iperbole in cui i due semiassi sono congruenti: a = b. In questo contesto ci sono alcune formule per gli elementi caratteristici della funzione omografica (intesa come iperbole equilatera) che possono risultare utili nella risoluzione degli esercizi. Le equazioni degli asintoti dell'iperbole equilatera sono dati da. y = (a)/(c) ; x = −(d)/(c) Il centro di simmetria ha coordinate: C = (−(d)/(c. Iperbole equilatera - teoria - YouTube 0:00 / 7:42 Iperbole equilatera - teoria Agostino Perna 34.5K subscribers Join Subscribe 1.9K views 2 years ago Iperbole Un rapido ripasso sulle. Iperbole equilatera Se nell'equazione canonica a = b l'iperbole si dice equilatera e la sua equazione può essere scritta nella forma: x 2 - y 2 = a 2 se i fuochi sono sull'asse x; x 2 - y 2 = - a 2 se invece i fuochi appartengono all'asse y. :: asintoti: y = - x , y = x (coincidono con le bisettrici dei quadranti) :: semidistanza focale: c = a 2
Asintoti di un iperbole FORMULE ed ESEMPI spiegati
Se un'iperbole equilatera viene riferita ai propri asintoti (e cioè se gli asintoti dell'iperbole coincidono con gli assi cartesiani), allora la sua equazione assume una forma molto semplice:. In entrambe le formule è detto semiasse trasverso o semiasse maggiore; è la metà della distanza tra i due rami; è chiamato. nell'iperbole equilatera gli asintoti coincidono con le bisettrici del I e III e del II e IV quadrante iperbole equilatera ruotata di funzione omografica Si dice funzione omografica, l'iperbole equilatera ruotata di e traslata rispetto all'origine degli assi cartesiani equazione coordinate di equazioni asintoti F 1 F 2 a a Vediamo come rappresentare l' iperbole equilatera riferita agli asintoti e l'iperbole traslata. Vedremo inoltre come fare a trovarne l'equazione e le coordin. Iperbole in Geometria Analitica : Introduzione Elia Bombardelli 505K subscribers 329K views 8 years ago Ellisse ed Iperbole in Geometria Analitica Vediamo come si definisce e come si.

Equazione iperbole teoria e formule
Possiamo quindi avere una iperbole equilatera con fuochi sull'asse x, o un iperbole equilatera con fuochi sull'asse y. Lo svolgimento dell'esercizio del grafico di un iperbole equilatera si rifà dunque ai due esercizi già fatti, con l'unica differenza che nelle formule avete un solo coefficiente, visto che a=b. Successivamente si introduce il concetto di asintoto, concentrandosi sugli asintoti verticali e orizzontali, e si illustra il nesso tra proporzionalità inversa e asintoti: l'iperbole equilatera, che rappresenta la proporzionalità inversa, ha sempre un asintoto verticale e uno orizzontale.
L' equazione dell'iperbole individua l'iperbole come luogo geometrico dei punti del piano per i quali la differenza delle distanze da due punti fissi, detti fuochi, resta costante. Poiché tutte le definizioni e le formule dell'iperbole sono proposte nell'omonimo formulario qui mi limiterò ad una panoramica sull'equazione dell'iperbole e a mostrarti un paio di esempi di esercizi in cui è. In un' iperbole equilatera le misure dei semiassi coincidono, ovvero a = b. La sua equazione pertanto è del tipo: x 2 - y 2 = a 2. nel caso in cui intersechi l'asse delle ascisse, oppure. x 2 - y 2 = -a 2. nel caso in cui intersechi l'asse delle ordinate. Se invece l'iperbole è tale per cui i suoi asintoti corrispondono agli assi.
Iperbole equilatera equazione, asintoti, disegno ed ESEMPI
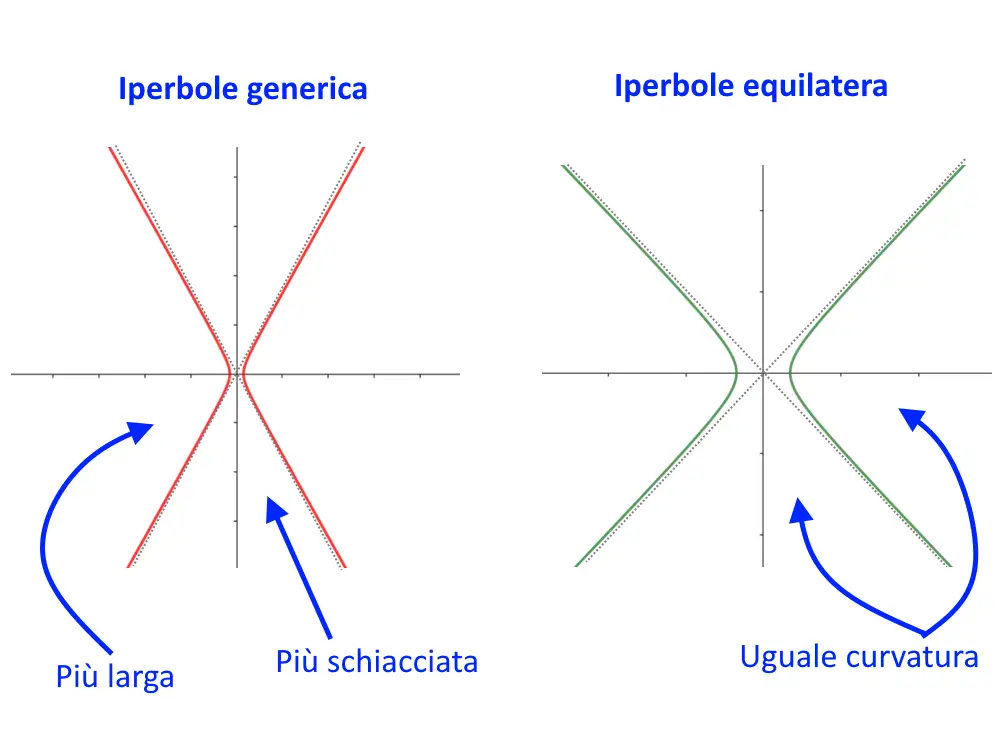
Eccentricità dell'iperbole equilatera. Calcolare l'eccentricità è fondamentale per capire il significato di "equilatera". La formula dell'eccentricità ricordiamo essere in un iperbole generica: e = \frac {\sqrt {a^2 + b^2} } {a} e = aa2+b2. Ma nel caso di una iperbole equilatera, noi abbiamo i coefficienti uguali, ossia a^2 = b^2. Definizione di iperbole ed equazione dell'iperbole con asse reale o trasverso, disposto sull'asse x (con fuochi sull'asse x e vertici reali sull'asse x) e quella con asse non trasverso disposto sull'asse y (con fuochi sull'asse y e vertici reali sull'asse y) Formule per trovare Vertici, Fuochi, eccentricità e asintoti dell'iperbole




