I limiti notevoli sono particolari limiti di funzioni elementari ricorrenti che vengono dimostrati una volta per tutte e che vengono dati per buoni nel calcolo dei limiti. In altri termini, i limiti notevoli possono essere usati come risultati assodati nel calcolo di limiti più complessi che li coinvolgono. Limiti notevoli in un limite con seno e tangente Ho un limite con seno e tangente da risolvere ricorrendo ai limiti notevoli, almeno questo suggerisce il libro. lim_ (x → 0) (2x+sin (4x))/ (tan (x)) Come posso risolverlo? Grazie in anticipo a chi mi risponderà. Domanda di Fede180910 Soluzione Il limite è lim_ (x → 0) (2x+sin (4x))/ (tan (x))

Limiti Notevoli Esercizi di Analisi Matematica 1 Michele Di Luca
12) Limite notevole associato: lim_ (x → 0) (tan (x))/ (x) = 1 13) Derivata della tangente: (d)/ (dx)tan (x) = (1)/ (cos^2 (x)) 14) Integrale della tangente: ∫tan (x)dx = −ln (|cos (x)|)+c Limite notevole della tangente lim x → 0 tan ( x) x = 1 Limite notevole della potenza con differenza lim x → 0 ( 1 + x) k − 1 x = k, k ∈ R Sono qui presentati alcuni limiti notevoli utilizzati per una risoluzione più veloce di limiti che possono sembrare poco immediati. Tali limiti sono anche usati nell'applicazione del principio di sostituzione degli infinitesimi equivalenti. Scriviamo la tangente sfruttando la sua definizione di rapporto tra seno e coseno dell'angolo: 3. Forum In questo capitolo prenderemo in considerazione le seguenti funzioni trigonometriche: seno coseno tangente cotangente Limiti delle funzioni seno e coseno Consideriamo i seguenti tipi di limiti: limite in un determinato punto (ad esempio ) limite all'infinito. Limite della funzione in un punto

Limiti Con Taylor Esercizi Svolti loneighton
Formulario limiti notevoli: tabella dei limiti notevoli o fondamentali, in uno schema per risolvere gli esercizi riconducendosi ai limiti immediati di funzione Come nel caso dei prodotti notevoli, i limiti notevoli ci permettono di semplificare e velocizzare i calcoli, in modo da risolvere velocemente i nostri limiti: Solitamente, per risolvere un limite, la strada più veloce è quella di semplificare Facciamo un esempio: lim x→3 2x = 2⋅ 3 = 6 lim x → 3 2 x = 2 ⋅ 3 = 6 Limiti Notevoli: Tabella. funzioni goniometriche. funzioni goniometriche. s e n x l i m = 1. x → 0. x. tg x lim = 1. x → 0. x. Home - Limiti di funzioni In questa lezione ci occupiamo di fornire le dimostrazioni dei limiti notevoli fondamentali, ovvero il limite notevole del seno e il limite notevole di Nepero. La dimostrazione del limite notevole del seno si basa in prevalenza su considerazioni di carattere geometrico.

Esercizi Svolti Sui Limiti Notevoli Trigonometrici Matematica Oltre
Ciao ragazzi!In queso video vediamo la dimostrazione del più classico dei limiti notevoli.sfrutteremo un pò di trigonometria e il teorema del confronto----. Limiti notevoli: definizione, tabella e risoluzione. Argomento valido per: Scuola superiore. Scritto da Valerio Panetta. Il limite di funzione è un argomento molto utile in matematica e serve per capire come si comporta una funzione vicino a un punto del suo dominio. Molte volte, nel calcolo del limite, ci imbattiamo in delle forme indeterminate.
In conclusione, i limiti notevoli sono uno strumento importante nell'analisi matematica per calcolare il valore di una funzione quando l'argomento si avvicina a un particolare punto. Attraverso una serie di esercizi , abbiamo visto come applicare i limiti notevoli a diverse funzioni, tra cui la tangente, l'esponenziale, la funzione. Limite notevole dell'arcotangente lim x → 0 arctan ( x) x = 1; lim f ( x) → 0 arctan ( f ( x)) f ( x) = 1 Limite notevole del seno iperbolico lim x → 0 sinh ( x) x = 1; lim f ( x) → 0 sinh ( f ( x)) f ( x) = 1
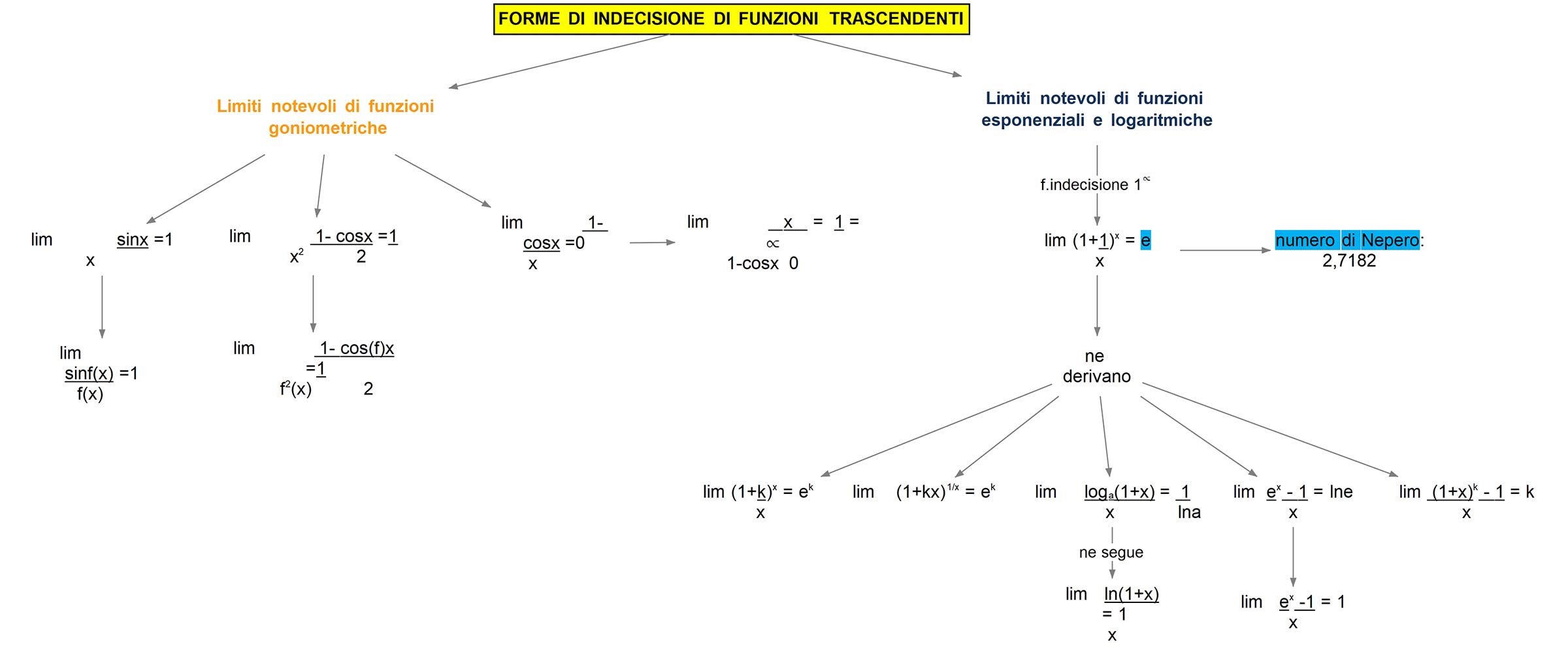
limiti notevoli Mappa concettuale
Esercizi Analisi 1 Esercizi sui limiti Qui di seguito vi proponiamo la prima di due schede di esercizi risolti sui limiti notevoli, tutti interamente svolti e commentati in ogni singolo passaggio. Ovviamente i limiti notevoli qui sono i protagonisti. v.scudero appunti di analisi matematica - limiti notevoli cos ≤ ≤1 x senx x Al tendere di x → 0 le quantità esterne tendono entrambe a 1 (limcos 1 0 = → x x e la funzione y=1 è costante) per cui, per il teorema del confronto (cfr. T3.3) anche la quantità interna tende allo stesso valore. c.v.d. 2. Il numero di Nepero "e"




