Per definizione un triangolo isoscele è un triangolo con due lati congruenti. In alternativa, ed equivalentemente, possiamo affermare che un triangolo isoscele è un triangolo con due angoli di uguale ampiezza. È bene precisare che i triangoli isosceli sono frutto di una classificazione dei triangoli in base ai lati e non agli angoli. Formule da applicare per calcolare la mediana di un triangolo di qualsiasi tipologia. La prima m (a) = ½√2 (AC² + AB²) - BC². La seconda m (b) = ½√2 (BC² + AB²) - AC². Infine, la terza.

Triangolo Isoscele definizione, formule e proprietà μatematicaΘk
Nel corso della spiegazione noterete che a ogni segmento notevole è associato un particolare punto: all'altezza di un triangolo è associato l'ortocentro, alla bisettrice l'incentro, alla mediana il baricentro e all'asse il circoncentro. Tali punti sono detti punti notevoli del triangolo e li trattiamo nel dettaglio nella lezione successiva. Di conseguenza: A O ( = O V + V A) = 2 ⋅ K O. B O ( = O W + W B) = 2 ⋅ Q O. Ripetendo le stesse considerazioni anche per le coppie mediane AK e CH, e poi BQ e CH, otterremo risultati del tutto. I triangoli isosceli sono quelli con due lati congruenti. Se un triangolo è isoscele, allora ha (anche) due angoli congruenti. Per dimostrare il teorema del triangolo isoscele tracciamo la bisettrice dell'angolo opposto alla base e troviamo così due nuovi triangoli, a questi applichiamo il primo criterio di congruenza per concludere che i. Proprietà. Alcune proprietà della mediana: 1 - Il triangolo viene diviso dalla mediana in due triangoli aventi la stessa superficie e tutte le altre rette che dividono il triangolo in due parti di uguale superficie non passano per il baricentro.. 2 - Le tre mediane di un triangolo si intersecano in un punto chiamato baricentro o centro di massa (per una dimostrazione si veda per esempio il.

Teorema del triangolo isoscele YouTube
Se in un triangolo l'altezza, la mediana e la bisettrice condotte dal vertice opposto alla base sono coincidenti allora il triangolo e' isoscele. Per esercizio fai la dimostrazione. Siccome abbiamo un teorema ed anche il suo inverso d'ora in avanti i fatti. triangolo isoscele <=> altezza=mediana=bisettrice. saranno equivalenti. TEOREMA DIRETTO DEL TRIANGOLO ISOSCELE. Teorema: " un triangolo isoscele ha gli angoli alla base uguali ". Ipotesi: è dato un triangolo ABC del quale sappiamo che i lati AB e AC sono uguali. La bisettrice di un triangolo isoscele relativa all'angolo al vertice coincide con altezza, mediana e asse relativi alla base. Ci sono alcuni triangoli che si possono considerare triangoli isosceli particolari. Essi sono: triangoli equilateri, triangoli rettangoli isosceli. Esistono anche triangoli isosceli ottusangoli e acutangoli. Teoremi del triangolo isoscele. Il triangolo isoscele ha almeno due lati congruenti, l'eventuale lato non congruente si chiama base, i due lati congruenti si dicono lati obliqui. Il triangolo equilatero è un caso particolare di triangolo isoscele: si dice che il triangolo equilatero è isoscele rispetto a qualsiasi lato preso come base.

All'interno un triangolo isoscele abc con base. Teoria dettagliata con
Misura la lunghezza della mediana utilizzando un righello o un metro. La mediana sarà uguale alla distanza tra il vertice superiore e il punto medio del lato opposto. È importante ricordare che la mediana di un triangolo isoscele divide il lato opposto in due segmenti di lunghezza uguale. Esempio: Supponiamo di avere un triangolo isoscele con. Teorema del triangolo isoscele e sua dimostrazione; uguaglianza tra mediana, altezza e bisettrice relative alla base di un triangolo isoscele
Triangolo isoscele. In geometria, si definisce triangolo isoscele un triangolo che possiede due lati congruenti.. Vale il seguente teorema: "Un triangolo è isoscele se e solo se ha due angoli congruenti".Questo teorema costituisce la quinta proposizione del Libro I degli Elementi di Euclide ed è noto come pons asinorum.. In un triangolo isoscele la bisettrice relativa all'angolo al vertice. Una spiegazione più dettagliata sulle altezze nei triangoli equilatero e isoscele. La caratteristica dell'altezza, della mediana e della bisettrice in questo.
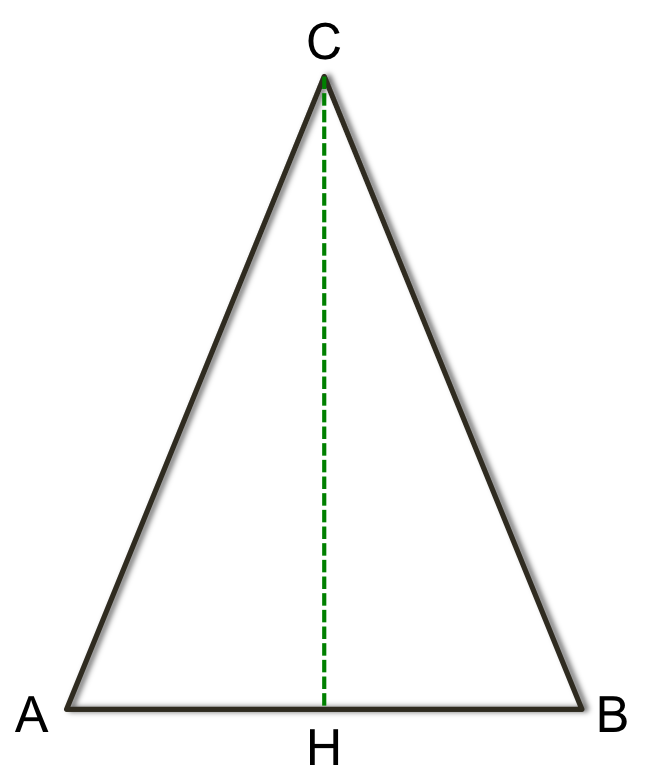
Problema Triangolo Isoscele (calcolo perimetro e area conoscendo base
Triangoli Mediana e baricentro. Primo e secondo criterio di congruenza dei triangoli. Teorema: "Un triangolo isoscele ha gli angoli alla base congruenti"🍀. Formule del Triangolo isoscele: area, perimetro, base, altezza, lato obliquo. Disegno, definizione e proprietà.




