La mediana relativa all'ipotenusa Agostino Perna 40.3K subscribers 21K views 5 years ago geometria razionale In un triangolo rettangolo la mediana relativa all'ipotenusa è congruente a metà. 15 - Somma degli angoli interni di un poligono (animazione) 16 - La somma degli angoli esterni di un poligono convesso. 17 - Quarto criterio di congruenza. 18 - La mediana relativa all'ipotenusa. 19 - La distanza tra due rette parallele.
Mediana relativa all'ipotenusa GeoGebra
Lunghezza della mediana relativa all'ipotenusa relativa all'ipotenusa è metà dell'ipotenusa stessa. TEOREMA In un triangolo rettangolo, la mediana DIM. Costruzione: prolungo la mediana AM di un segmento MD = AM . Congiungo D con B. I due triangoli AMC e DMB sono uguali per il 1° Criterio: MC = BM per ipotesi, AM = MD per costruzione, AMC l = DMB l perché opposti al vertice. Se la mediana è quella relativa all'ipotenusa è la metà di essa e quindi l'ipotenusa sarà il doppio: i = 13 x 2 = 26 cm Per capire meglio si deve fare il disegno di un rettangolo qualsiasi e tracciare le due diagonali e si può vedere che, cancellando uno dei due triangoli rettangoli, rimane una diagonale a metà e questa è la mediana perché la mediana relativa all'ipotenusa è metà dell'ipotenusa stessa; l'altezza relativa a un cateto coincide con l'altro cateto; l' ortocentro del triangolo coincide con il vertice dell'angolo retto; il circocentro del triangolo coincide con il punto medio dell'ipotenusa. Veniamo alle formule relative a un triangolo rettangolo generico.

TEOREMA DE LA MEDIANA RELATIVA A LA HIPOTENUSA YouTube
Geometria Geometria Piana Un triangolo rettangolo è un triangolo in cui uno degli angoli interni è un angolo retto (90°). I due lati perpendicolari di un triangolo rettangolo vengono detti cateti, mentre il lato opposto all'angolo retto è detto ipotenusa. Calcoliamo la lunghezza della mediana relativa all'ipotenusa. Ricordiamo che la mediana è il segmento che congiunge il punto medio d'un lato con il vertice opposto, calcoliamo le coordinate del punto medio di BC: x_M = (x_B+x_C)/ (2) = (3−8)/ (2) = − (5)/ (2) 2) L'altezza relativa all'ipotenusa è anche mediana e bisettrice, quindi: - il punto di intersezione tra altezza e ipotenusa è punto medio dell'ipotenusa; di conseguenza le proiezioni dei due cateti sull'ipotenusa sono segmenti congruenti; - l'altezza divide l'angolo retto in due angoli congruenti, ciascuno ampio 45°. la bisettrice è isoscele dell'angolo al vertice è mediana e altezza relativa In un la triangolo Vale anche: è bisettrice dell'angolo al vertice e altezza relativa alla base è mediana alla base e bisettrice dell'angolo al Se un triangolo è equilatero I teorema sul triangolo equilatero allora gli angoli sono tutti congruenti

TEOREMA DE LA MEDIANA RELATIVA A LA HIPOTENUSA CONGRUENCIA DE
le misure di due lati (relative ai due cateti oppure ad un cateto e all'ipotenusa); l'area del triangolo e la misura di un cateto; informazioni sulle somme e/o differenze tra le misure dei lati e sui rapporti tra le misure dei lati. Ricordiamo che per misura di un lato si intende la lunghezza del segmento ad esso corrispondente. Formule del Triangolo rettangolo: area, perimetro, ipotenusa, cateti, teorema di Pitagora. Disegno, definizione e proprietà.
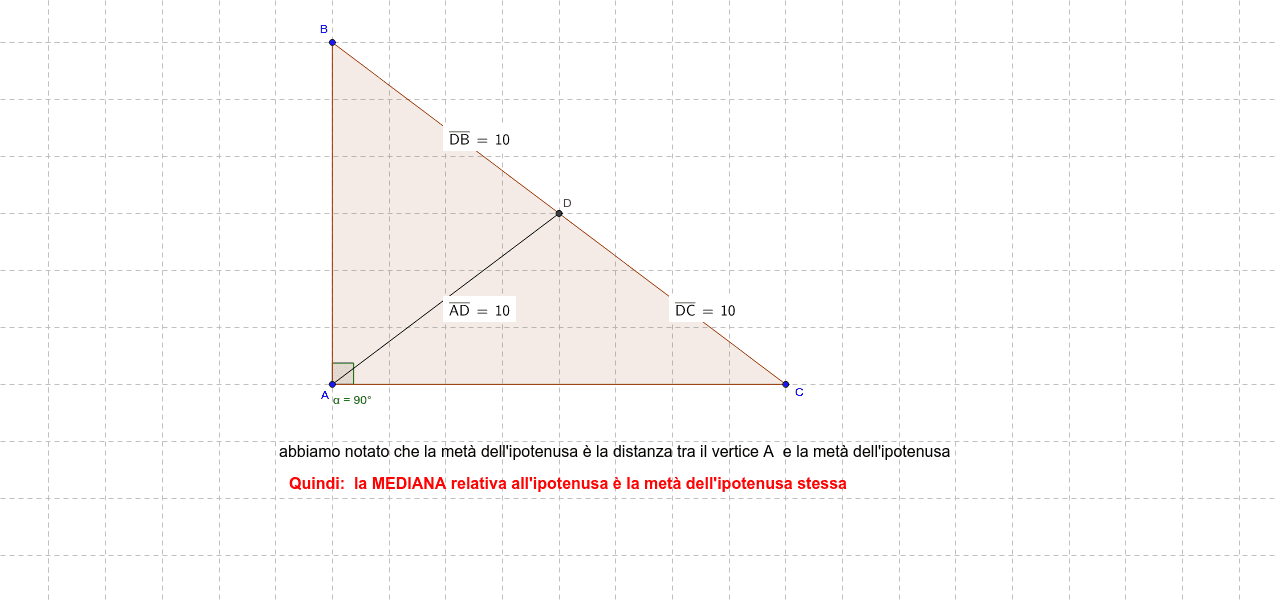
L' ipotenusa è il lato di un triangolo rettangolo opposto all'angolo di 90°; dato un triangolo rettangolo ABC con angolo retto in A, l'ipotenusa è il lato BC opposto ad esso e si calcola mediante il teorema di Pitagora come BC=√ (AB^2+CA^2). Come riconoscere l'ipotenusa in un triangolo rettangolo La mediana relativa all'ipotenusa è un concetto geometrico utilizzato nel contesto dei triangoli rettangoli. Quando si parla di mediana relativa all'ipotenusa, ci si riferisce ad una particolare linea che congiunge il vertice dell'angolo retto di un triangolo rettangolo con il punto medio dell'ipotenusa. La mediana relativa all'ipotenusa.

CRITERI DI CONGRUENZA DEI TRIANGOLI RETTANGOLI, mediana relativa all
La mediana relativa all'ipotenusa. La mediana relativa all'ipotenusa è un concetto geometrico utilizzato nel contesto dei triangoli rettangoli. Quando si parla di mediana relativa all'ipotenusa, ci si riferisce ad una particolare linea che congiunge il vertice dell'angolo retto di un triangolo rettangolo con il punto medio dell'ipotenusa. Teorema de la mediana en el triángulo rectángulo, demostración y problemas resueltos.Aplicaciones de la congruencia de triángulos. #geometría Bienvenido! Est.




