Qui di seguito elenchiamo tutte le formule dell'area di un quadrato. Indichiamo con A l'area, con L la misura del lato, con 2p il perimetro e con d la misura della diagonale. Dati. Formula. Area del quadrato con il lato. A = L^2. Area del quadrato con il perimetro. A = ( (2p)^2)/ (16) Area del quadrato con la diagonale. Oggi parliamo di geometria del piano, la materia che studia le figure a due dimensioni.Per farlo partiamo da quella più semplice in assoluto, il quadrato, con una spiegazione facile da capire, alcuni esempi e le formule per calcolare l'area e il perimetro. Il quadrato è un quadrilatero regolare, lo si riconosce facilmente perché è formato da quattro lati che sono tutti uguali, cioè della.

Pin su matematica
Formule del Quadrato: area, perimetro, lato, diagonale. Disegno, definizione e proprietà. Per calcolare il perimetro del quadrato dall'area si deve estrarre la radice quadrata dell'area e moltiplicare il risultato per 4. 2p = 4 √(A) Esempio. Calcolare il perimetro di un quadrato la cui area è di 25 metri quadrati. 2p = 4 √(A) = 4·√(25 m^2) = 4·(5 m) = 20 m. Per cominciare proponiamo la definizione e le formule del quadrato, comprese le formule inverse, utili nella risoluzione dei problemi e degli esercizi: area, diagonale, perimetro, lato e così via. Successivamente passiamo a elencarne le proprietà e mettiamo in mostra le principali relazioni con le altre figure piane in Geometria. L è il lato del quadrato; d è la diagonale del quadrato; A corrisponde all'area del quadrato; 2p è il perimetro del quadrato. Formula perimetro del quadrato. 2p = 4L 2 p = 4 L. Formula lato del quadrato con il perimetro. L = 2p 4 L = 2 p 4. Formula area del quadrato con il lato.

Perimetro e area del quadrato
Moltiplica la misura del perimetro per 1/4, in modo da individuare la lunghezza di un singolo lato. Questa operazione corrisponde a dividere il perimetro per il numero 4. Dato che il quadrato è un parallelogramma speciale, in cui tutti i lati sono uguali, partendo dal perimetro puoi risalire facilmente alla lunghezza dei lati dividendolo per 4. In questa lezione vediamo le caratteristiche del quadrato, come si calcola la misura del perimetro, dell'area e della diagonale con alcuni esempi pratici. L'area e il perimetro del quadrato. I lati del quadrato sono della stessa lunghezza, i latti adiacenti formano un angolo retto. Le diagonali sono della stessa lunghezza, si dividono mutuamente a metà e sono perpendicolari. quadrato. 3. Moltiplica il valore del lato per 4 e otterrai il perimetro. Prendi la lunghezza s che hai appena ricavato e inseriscila nella formula del perimetro: P = 4s! Per il quadrato di area pari a 20 e lato 4,472, il perimetro è P = 4 * 4,472 cioè 17,888. Per il quadrato di area pari a 25 e lato 5, il perimetro è P = 4 * 5 cioè 20.
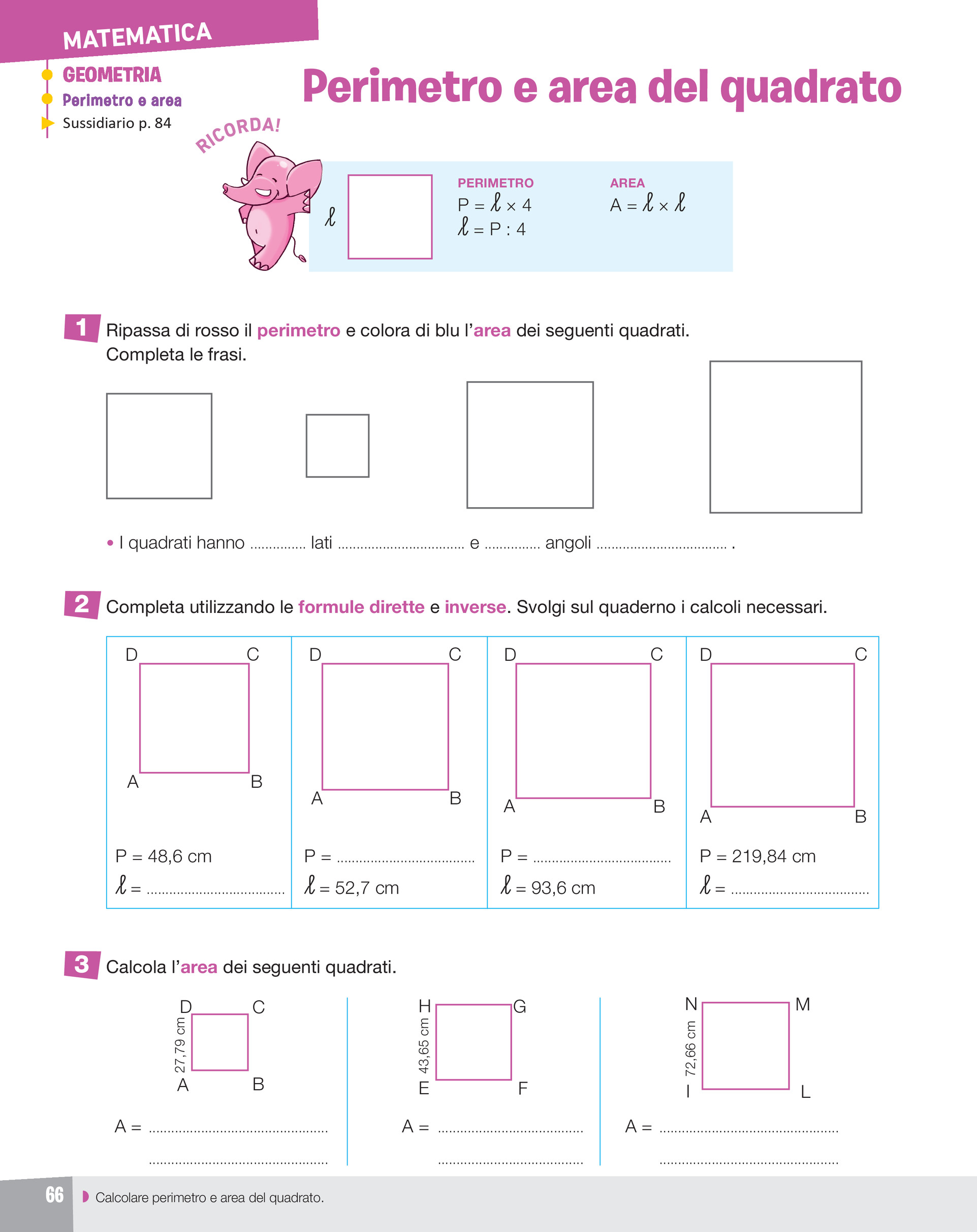
Perimetro e area del quadrato
Scoprite come calcolare area e perimetro del quadrato, scaricate le schede didattiche (per la scuola primaria) e gli esercizi interattivi.. Il quadrato 1.1 Formule. Perimetro . 2p = 4 x l . Area. A = l x l . 1.2 Proprietà. Lati . Il quadrato ha 4 lati uguali tra loro. Angoli. I 4 angoli interni del quadrato sono tutti uguali e sono angoli. Proponiamo delle schede per favorire la capacità dei bambini di calcolare il perimetro e l'area del quadrato. Destinatari: bambini della scuola primaria. Questa attività favorisce: la capacità di calcolare il perimetro e l'area del quadrato. Materiale occorrente: fogli A4, pastelli.
Problema 4: calcola l'area di un quadrato che ha il perimetro lungo 116 cm. Dati: Richieste: Perimetro = 116 cm. Area? Per determinare l'area del quadrato è necessaria la misura del suo lato: avendo la misura del perimetro, questo problema si svolge applicando la formula inversa del perimetro del quadrato , ottenendo: Studiamo le formule per il calcolo di area e perimetro delle tre principali figure geometriche: quadrato, rettangolo e triangolo. Indichiamo qui di seguito A A per l'area e 2p 2p per il perimetro. Quadrato di lato l l: A= (l)^2 A = (l)2. 2p= 4l 2p = 4l.

Schede di geometria il quadrato (perimetro e area) Fantavolando
Per quanto detto nella definizione, quindi, un quadrato è contemporaneamente un rettangolo e un rombo. Inoltre, essendo equiangolo (cioè, con tutti gli angoli congruenti) ed equilatero (cioè, con tutti i lati uguali), è un poligono regolare. Ciascun angolo interno del quadrato misura $\frac{\pi}{2}$ radianti, cioè $90^\circ$. Perimetro quadrato: O = 4 × a [m] Area quadrato: P = a × a = a² [m²] Diagonale quadrato: u = a √2 ≈ a × 1,41 [m] a. Lato del quadrato. u. Diagonale. Il rappporto tra quadrato e cerchio. Diagonale (u) = diametro della circonferenza circoscritta Lato del quadrato (a) = diametro della circonferenza inscritta


