Prodotti: il prodotto è l'operazione di moltiplicazione. E fin qua non c'è nulla di difficile. Sappiamo quindi che si tratta di eseguire una o più moltiplicazioni. Notevoli: l'unica cosa che hanno di notevole questi prodotti è la loro frequenza. Mi spiego meglio. Si tratta di moltiplicazioni che capita spesso di incontrare. 18K 875K views 6 years ago Monomi e Polinomi : Calcolo Letterale Vediamo cosa si intende per prodotti notevoli e come svolgere il quadrato di un binomio e la somma per differenza =).

Prodotti notevoli Quadrato di un binomio YouTube
Prodotti notevoli: Quadrato di un binomio matematicaoggi 14.1K subscribers Subscribe 139 Share 9.6K views 7 years ago Prodotti notevoli Video lezione sul prodotto notevole quadrato di. 30 Prodotti Notevoli - Quadrato di un binomio BB Prof 50.6K subscribers 94K views 4 years ago Algebra We reimagined cable. Try it free.* Live TV from 100+ channels. No cable box or long-term. Cosa sono e a cosa servono i prodotti notevoli?Dimostreremo poi la regola del quadrato di un binomio, ovvero un binomio elevato alla seconda.Infine tre eserc. Il quadrato di un binomio è il prodotto notevole (A±B) 2 =A 2 ±2AB+B 2 e si calcola come quadrato del primo monomio, più o meno il doppio prodotto dei due monomi, più il quadrato del secondo monomio.

Prodotti notevoli il quadrato di un binomio Matematica Facile
I prodotti notevoli sono formule di calcolo che permettono di sviluppare velocemente determinate potenze e prodotti tra polinomi, e viceversa di scomporre determinati tipi di polinomi. Tali regole vengono chiamate prodotti notevoli perché si riferiscono a prodotti ricorrenti nel calcolo polinomiale. In simboli matematici, tale prodotto notevole si esprime come: (A+B)^2 = A^2+2AB+B^2 Alla luce di ciò, applichiamo la formula per sviluppare il quadrato ( (1)/ (2)x+ (3)/ (4)y^2)^2 = ( (1)/ (2)x)^2+2· ( (1)/ (2)x)· ( (3)/ (4)y^2)+ ( (3)/ (4)y^2)^2 = Qui si seguito i prodotti notevoli più importanti e comunemente utilizzati: Il quadrato di binomio con somma e il quadrato di un binomio con differenza: (a +b)2 = a2 + 2ab+ b2 ( a + b) 2 = a 2 + 2 a b + b 2. (a −b)2 = a2 − 2ab+ b2 ( a − b) 2 = a 2 − 2 a b + b 2. Il quadrato di un binomio è uguale al quadrato del primo termine, più il. #algebra #matematica #maths #scuola #prodotto

Prodotti notevoli. Quadrato di un binomio. Quadrato del trinomio
particolari del primo più prodotti il cubo del notevoli cubo del primo meno il cubo del secondo Prodotti notevoli oppure consideriamo il seguente esempio con n = 5, da potenza n-sima esso possiamo dedurre le regole di un binomio lo sviluppo della potenza n-sima di un binomio valide per ogni n La differenza di quadrati Tra i prodotti notevoli è il più difficile da riconoscere. Si ha quando in certi casi dove due binomi si devono moltiplicare fra loro. La condizione è che il primo binomio è la somma fra due monomi e il secondo la differenza fra gli stessi monomi. La formula di calcolo rapido è (a + b) (a - b) = a2 - b2.
Prodotti notevoli :come sviluppare il quadrato di un binomio . Dopo aver trattato i polinomi (playlist precedente ) e in particolare il prodotto tra due o più polinomi , è il momento. I prodotti notevoli sono formule ricorrenti di calcolo per i polinomi, che consentono la risoluzione immediata di prodotti e potenze tra polinomi. Le prime tre formule contengono esclusivamente termini al quadrato, per questo sono le prime ad essere apprese. Il primo prodotto notevole è il quadrato di binomio con somma di monomi: (a.
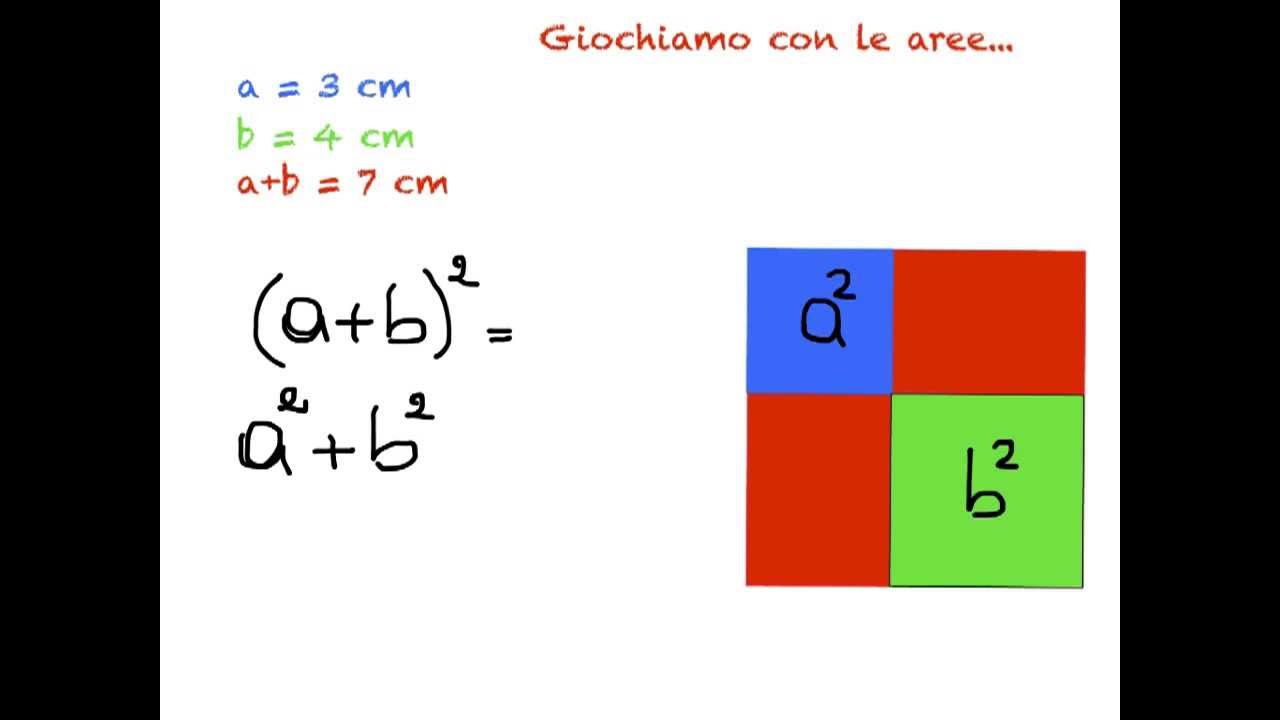
Prodotti notevoli Quadrato del binomio YouTube
Impara come usare i prodotti notevoli in matematica con questa lezione sul quadrato di binomio, trinomio e cubo di binomio. Con esempi pratici!. Il quadrato di un binomio è la formula che si ottiene quando si eleva al quadrato un binomio. La formula è: $$(a + b)^2 = a^2 + 2ab + b^2$$ Prodotti notevoli formule. Di seguito trovi un formulario con tutti i prodotti notevoli che si studiano a scuola. Puoi cliccare sul nome di ciascuno per aprire la lezione guida di approfondimento.. Il quadrato di binomio è pari al quadrato del primo termine più il doppio prodotto tra primo e secondo termine, più quadrato del secondo.



