Le funzioni iperboliche sono seno iperbolico, coseno iperbolico, tangente iperbolica, cotangente iperbolica, secante iperbolica e cosecante iperbolica, e costituiscono una famiglia di funzioni elementari dotate di proprietà analoghe a quelle delle funzioni goniometriche.. Questa pagina, più che una lezione, è una scheda di riepilogo sulle funzioni iperboliche in cui vedremo dapprima come si. L'argomento delle funzioni seno e coseno che definiscono la circonferenza può essere interpretato naturalmente come un angolo; la argomento delle funzioni iperboliche rappresenta invece due volte l'area del settore iperbolico compreso tra il segmento che collega l'origine con il punto (, ) su un ramo dell'iperbole equilatera di equazione.
funzione iperbolica inversa in "Enciclopedia della Matematica"
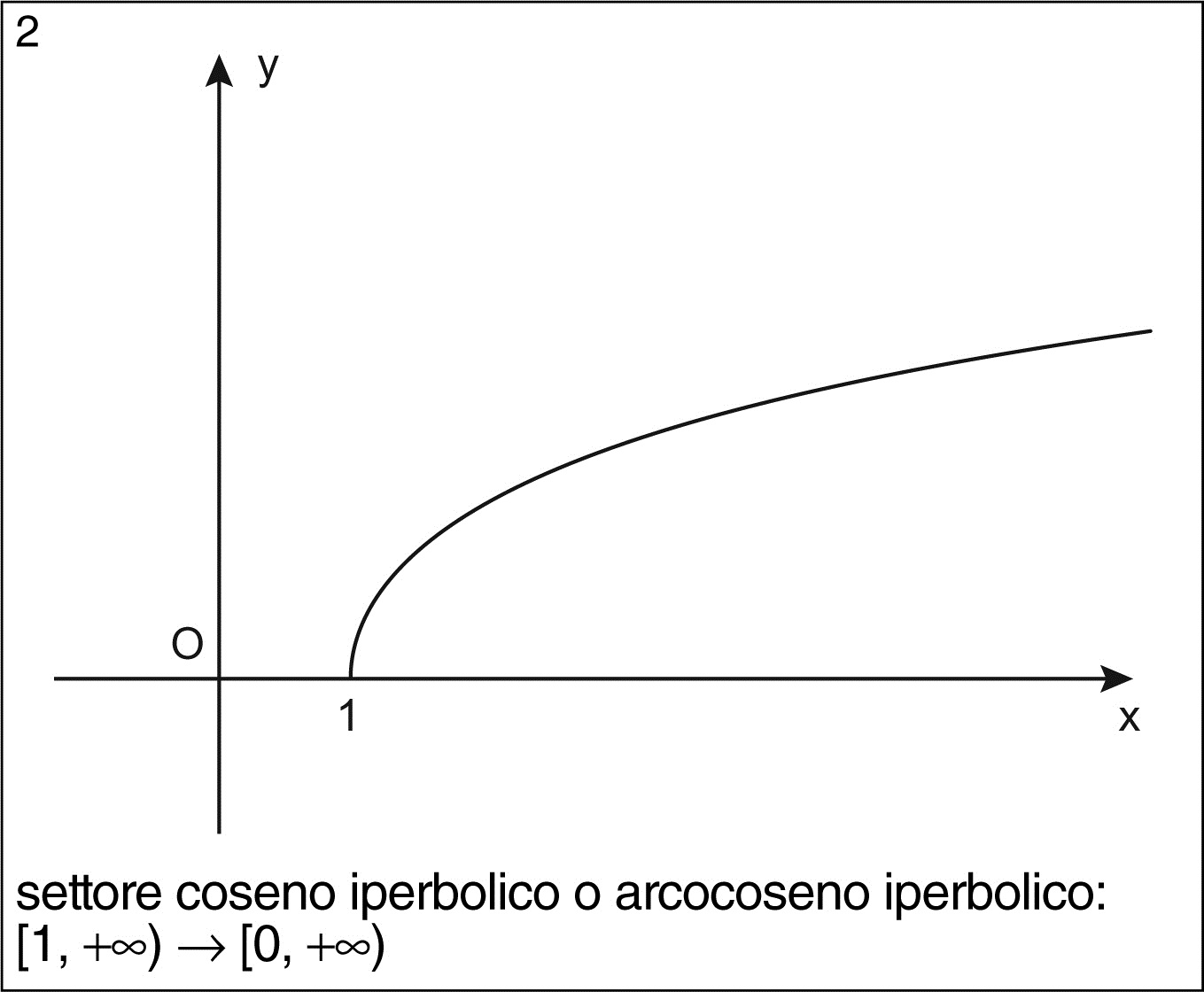
settore seno iperbolico settore seno iperbolico funzione inversa del seno iperbolico indicata con settsinh (ma talvolta anche con sinh−1 o con arcsinh) definita per ogni numero reale. Si ha: (Si veda anche → funzione iperbolica inversa). Si definisce settore seno iperbolico o arcoseno iperbolico di x la funzione: sett sinh(x) = arcsinh(x) = ln(x+√(x^2+1)) ∀ x∈R. ed è la funzione inversa della funzione seno iperbolico. Si definisce invece settore coseno iperbolico, o arcocoseno iperbolico di x la funzione: Il seno iperbolico sinh(x) è una funzione iperbolica, definita come differenza di esponenziali, così denominata per un interessante proprietà analoga all'identità fondamentale della Trigonometria che la lega all'equazione dell'iperbole.. Vediamo la definizione, le proprietà e il grafico del seno iperbolico, la prima delle funzioni iperboliche che trattiamo nella nostra rassegna. Ci interessiamo delle funzioni iperboliche inverse e delle loro proprietà. Va sottolineato che il logarirmo naturale è qui indicato con log, non con ln.

Qual é o cosseno hiperbólico? ⁉️
Il seno iperbolico è una funzione definita su tutto R e sempre crescente: è dunque invertibile su tutto R. La sua funzione inversa è detta arcoseno iperbolico e si denota comunemente con arcsinh. Si ha. Dalla seconda delle (3.9), ricordando che ey >0, si ha. e infine. Derivazione delle funzioni iperboliche. Voce principale: Funzioni iperboliche. L'equazione dell'iperbole equilatera in figura è: quindi: L'area del settore iperbolico è uguale all'area del triangolo meno l'area della regione del piano delimitata dall'arco di iperbole , dall'asse delle e dal segmento. Posto , si ha: La funzione seno iperbolico è crescente sul semiasse positivo, avvicinadosi indefinitamente a , perché lim → ˘ =0. La funzione seno iperbolico è crescente su tutto R. La monotonia della funzione è sufficiente ad assicurarne l'invertibilità. Ragionando sulla definizione ˆ= , si ottiene: −2ˆ− =0, e2x -2 y ex -1 = 0, Il seno iperbolico e il coseno iperbolico di un numero reale x sono legati dalla identità fondamentale cosh2 (x) − sinh2 (x) = 1. Il seno iperbolico è una funzione dispari, continua, differenziabile e illimitata: essa tende esponenzialmente a +∞ (rispettivamente −∞) per x tendente a +∞ (rispettivamente per x tendente a −∞); la sua.

La matematika in 100 schede versione 1.0 by Progetto matematika Issuu
Derivata delle funzioni iperboliche. Per calcolarne le derivate è sufficiente ricordare che Dxex = ex D x e x = e x e che in base alla regola della funzione composta è Dxe−x = −e−x D x e − x = − e − x; qui di seguito la procedura di calcolo della derivata del coseno iperbolico: In modo del tutto analogo si ricava la derivata del. Seno iperbolico e coseno iperbolico: le funzioni iperboliche. L'equazione x^2 + y^2 = 1 x2 + y2 = 1, nel piano cartesiano, descrive il luogo dei punti distanti 1 1 dall'origine degli assi: è la circonferenza unitaria centrata nell'origine. In trigonometria, questa circonferenza viene chiamata circonferenza goniometrica e in questo.
settore seno iperbolico settore coseno iperbolico settore tangente iperbolica settore cotangente iperbolica settore secante iperbolica settore cosecante iperbolica sviluppo in serie di Mac Laurin per alcune funzioni iperboliche funzione seno iperbolico. Data un'iperbole equilatera di equazione X²-Y²=1 centrata sull'origine degli assi cartesiani e dato un angolo α, andiamo a considerare il settore iperbolico disegnato in rosso di area α/2. Questo determina sull'iperbole un punto P. Si definisce seno iperbolico l'ordinata del punto P.. sinh(x)=y P. Le funzioni iperboliche vengono definite attraverso l'uso di funzioni esponenziali.

La Matematika in 100 schede versione 4.0 by Progetto matematika Issuu
funzione iperbolica funzione iperbolica particolare funzione definita a partire dalla funzione esponenziale. Le principali funzioni iperboliche sono le funzioni seno iperbolico, coseno iperbolico e tangente iperbolica, definite dalle identità: Similmente al caso goniometrico, si possono definire le altre funzioni iperboliche a partire dal coseno e dal seno iperbolici: la cotangente iperbolica. Le funzioni inverse delle funzioni iperboliche considerate sono rispettivamente settore seno iperbolico, settore coseno iperbolico, settore tangente iperbolica, settore cotangente iperbolica.




