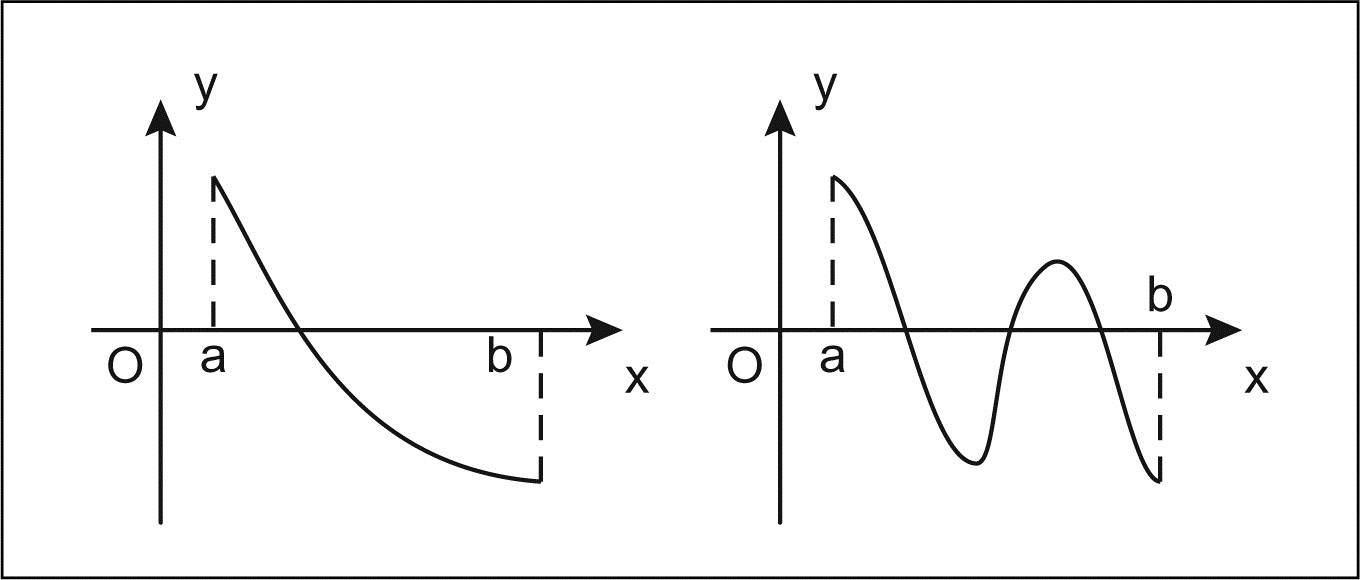
Il teorema degli zeri (detto anche teorema di Bolzano) è un risultato relativo alle funzioni continue il quale, sotto opportune ipotesi, stabilisce l'esistenza di almeno uno zero della funzione su un dato intervallo, ossia l'esistenza di almeno un punto in cui la funzione si annulla. Secondo il teorema di esistenza degli zeri ( o teorema di Bolzano) in una funzione f (x) continua in un intervallo [a,b] con f (a)<0 e f (b)>0 esiste un punto intermedio x 0 in (a,b) tale che f (x 0 )=0 ossia esiste una radice. Il teorema vale anche nel caso inverso, quando f (a)>0 e f (b)<0.

Teorema di Bolzano Weierstrass Appunti di analisi
Teorema di Bolzano In analisi matematica il teorema di Bolzano, detto anche teorema degli zeri per le funzioni continue, assicura l'esistenza di almeno una radice delle funzioni continue reali che assumano segni opposti ai due estremi di un intervallo. Vediamo l'enunciato del teorema di esistenza degli zeri ed un esempio di applicazione proveniente dai quesiti della maturità =) Si tratta di un importante teorema che si incontra. Il Teorema degli zeri è uno strumento che serve proprio a individuare una famiglia di funzioni per cui siamo certi esista almeno una radice. Come vedremo, ci sono anche funzioni che ammettono una o persino più radici, ma non soddisfano le ipotesi del nostro Teorema. Ci sono essenzialmente due tipi di richieste che in alcuni casi si presentano singolarmente e in altri sono accoppiate. La prima riguarda la sola e semplice esistenza degli zeri di funzioni, che a volte vengono interpretati come soluzioni di equazioni; la seconda riguarda l' approssimazione degli zeri.

[Modificato da ]
Bolzano teorema di esistenza degli zeri Luca Tomassini Sia f una funzione continua a valori reali su un intervallo chiuso [a,b] della retta reale ℝ e sia c un numero reale compreso tra f (a) e f (b). Il teorema di Bolzano, noto anche come teorema di Cauchy, stabilisce allora che esiste un punto x0∈ [a,b] tale che f (x0)=c. Arte Cataloghi TAG Teorema di esistenza degli zeri Funzione continua Intervallo Bolzano, teorema di Bolzano, teorema di detto anche teorema di esistenza degli zeri di una funzione, in analisi, stabilisce che una funzione c. zeri di una funzione, teorema di esistenza degli zeri di una funzione, teorema di esistenza degli stabilisce che una funzione continua in un intervallo [a, b], che assume valori discordi agli estremi di tale intervallo, si annulla in almeno un punto interno ad [a, b]. La dimostrazione di tale teorema si ottiene col metodo di → bisezione (dicotomia), ed è quindi costruttiva e particolarmente. Soluzione Per prima cosa enunciamo il teorema degli zeri: data una funzione f : [a,b] → R continua sull' intervallo chiuso e limitato [a,b] e tale da assumere agli estremi valori di segno opposto, cioè f (a)·f (b) < 0 allora esiste un punto x_0∈ (a,b) (estremi esclusi) tale che f (x_0) = 0. Controlliamo ora se la funzione f (x) = √ (x)+x^2−3
zeri di una funzione, teorema di esistenza degli in "Enciclopedia della
In questo video vengono enunciati e dimostrati il teorema di esistenza degli zeri ed il teorema di Darboux.http://www.ingcerroni.it/corsi-e-lezioni-private/ http://www.lezionidimate.it http://www.wikimate.it CLICCA SUL NOSTRO SITO PER L'INDICE COMPLETO DELLE VIDEOLEZIONITeorema di esistenza degli zeri
Oggi andremo a parlare del primo, che è il teorema di esistenza degli zeri: il teorema di esistenza degli zeri infatti dice che se la nostra funzione è continua in un intervallo chiuso a b da noi scelto e inoltre il prodotto tra f di a e f di b, quindi la funzione nell'estremo di sinistra per la funzione nell'estremo di destra è minore di zero,. Secondo il teorema di esistenza degli zeri, esiste un punto intermedio x 0 in cui la funzione è nulla. f (x0) = y f ( x 0) = y Essendo una funzione continua, la presenza del punto intermedio f (x 0) dimostra l'esistenza dei valori intermedi tra gli estremi f (a) e f (b) per qualsiasi x di [a,b]. Corollario di esistenza tra un minimo e un massimo

Teorema degli zeri Appunti di analisi matematica
teorema di esistenza degli zeri teorema di esistenza degli zeri Luca Tomassini Sia f una funzione continua a valori reali su un intervallo chiuso [a,b] della retta reale ℝ e sia c un numero reale compreso tra f(a) e f(b). Il teorema [.] , tale risultato è noto con il nome di teorema di esistenza degli zeri.La dimostrazione può essere realizzata a partire dal principio degli intervalli. In questa scheda forniamo la dimostrazione del teorema (di esistenza) degli zeri, di cui ripetiamo per comodita` l'enunciato. Teorema degli zeri Sia f una funzione definita e continua in un intervallo chiuso e limitato 1⁄2a, b . TEOREMA 4.5 Se fðaÞ fðbÞ < 0, allora la funzione ammette almeno uno zero in ða, bÞ, ossia esiste un punto x0 2 ða, bÞ


