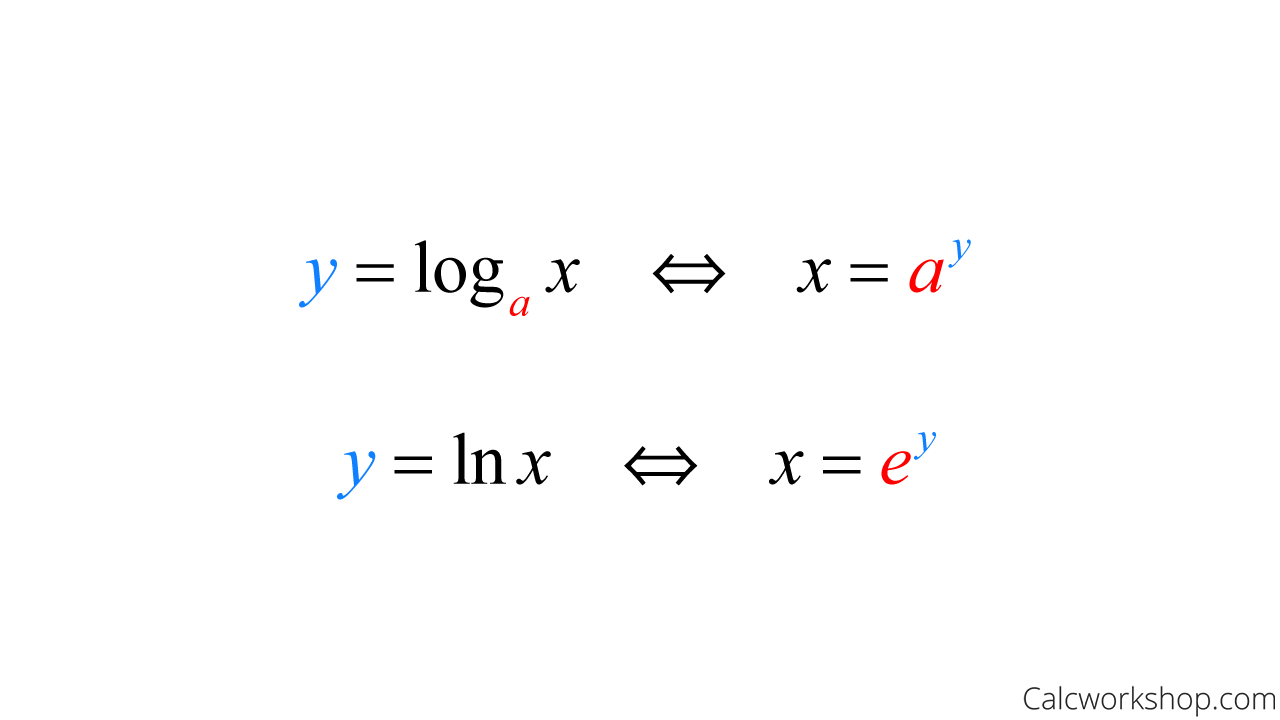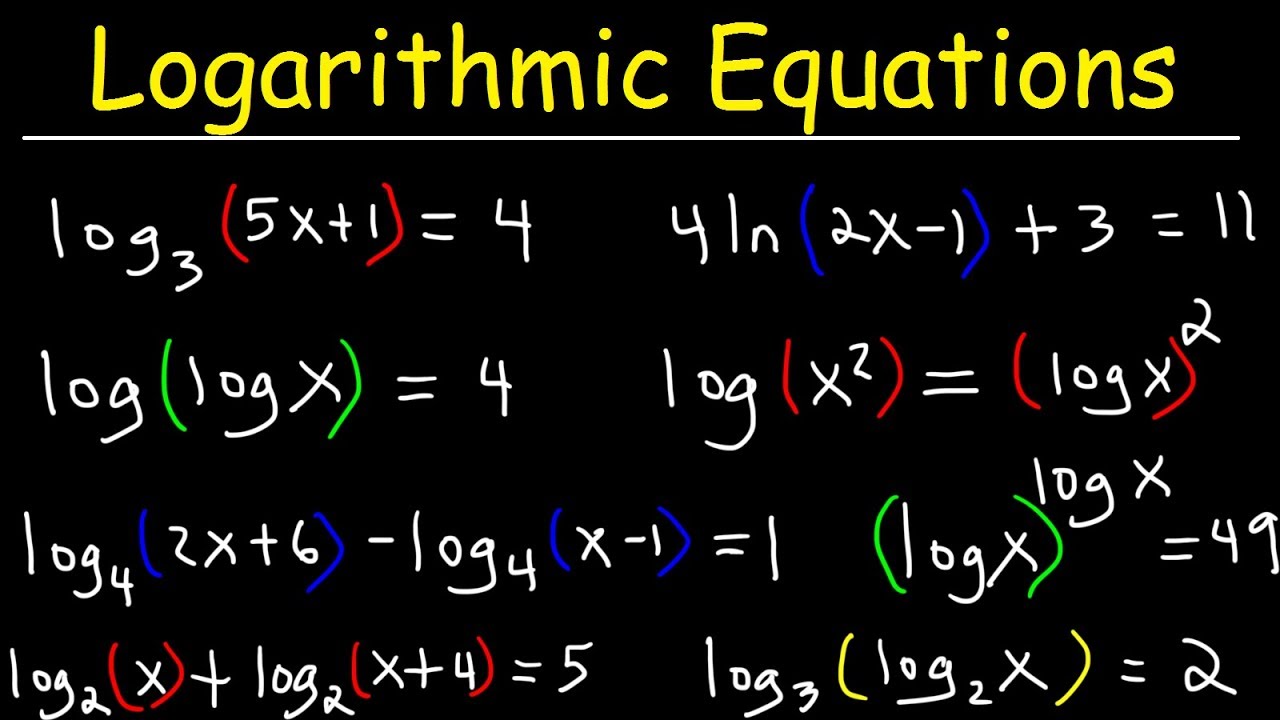Logarithm definition When b is raised to the power of y is equal x: b y = x Then the base b logarithm of x is equal to y: log b ( x) = y For example when: 2 4 = 16 Then log 2 (16) = 4 Logarithm as inverse function of exponential function The logarithmic function, y = log b ( x) is the inverse function of the exponential function, x = by Logarithms, like exponents, have many helpful properties that can be used to simplify logarithmic expressions and solve logarithmic equations. This article explores three of those properties. Let's take a look at each property individually. The product rule: log b ( M N) = log b ( M) + log b ( N)

a^log x base a=x a^log x base a proof logarithm YouTube
In mathematics, the logarithm is the inverse function to exponentiation. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 103, the logarithm base 10 of 1000 is 3, or log10 (1000) = 3. This identity is useful to evaluate logarithms on calculators. For instance, most calculators have buttons for ln and for log 10, but not all calculators have buttons for the logarithm of an arbitrary base.. Proof/derivation. Let , +, where , Let +.Here, and are the two bases we will be using for the logarithms. They cannot be 1, because the logarithm function is not well defined for the base. Definition of a logarithm Generalizing the examples above leads us to the formal definition of a logarithm. log b ( a) = c b c = a Both equations describe the same relationship between a , b , and c : b is the base , c is the exponent , and a is called the argument . A helpful note log(x) Natural Language; Math Input; Extended Keyboard Examples Upload Random. Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music…
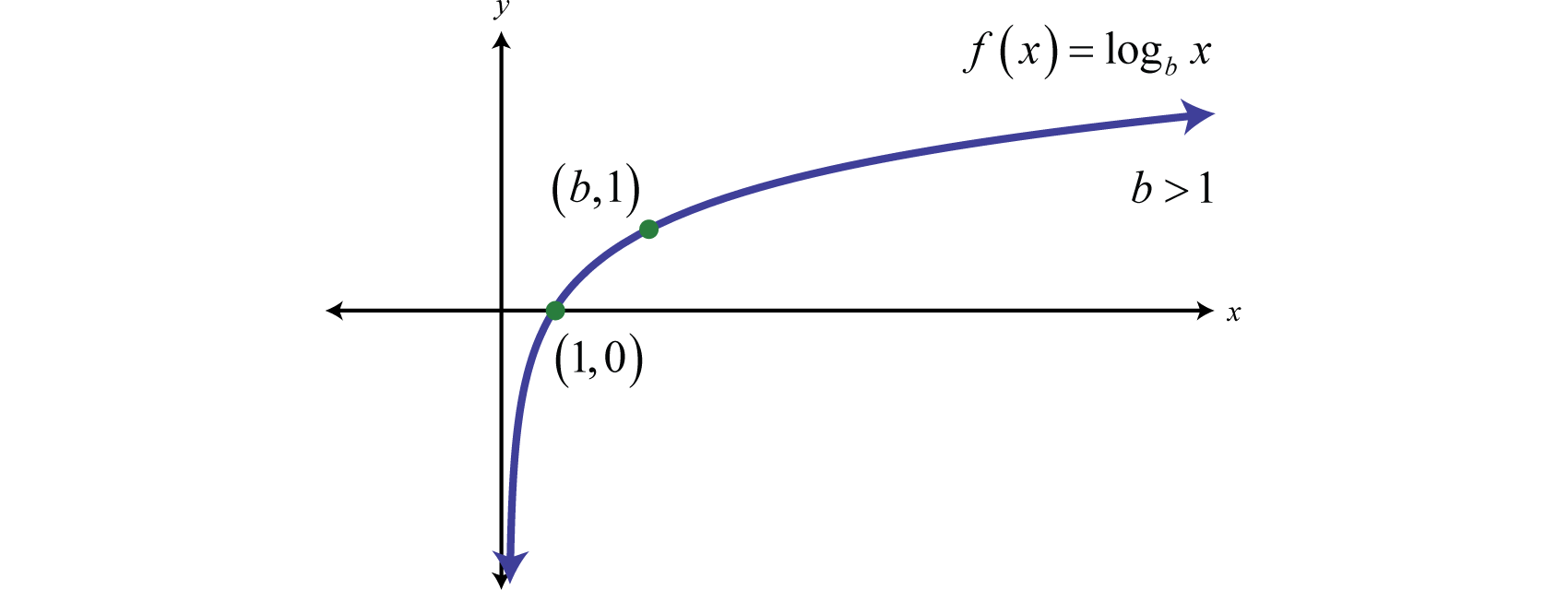
Logarithmic Functions and Their Graphs
log(a)log(x) = log(a)log(x) log ( a) l o g ( x) = log ( a) log ( x) This is essentially another way of saying what sanjab has already said, but in a way that gives it a bit more intellectual context. Its sort of the "deeper reason" why it works. So why does plog(q) qlog(p) p log ( q) = q log ( p)? 4 Answers. By definition, the log − log − function is the inverse of the exponential function. It means that, if f: R →R+ f: R → R + such that, f(f−1(x)) = x. f ( f − 1 ( x)) = x. We then define f−1 f − 1 as f−1(x) =loga x f − 1 ( x) = log a x. So, f(f−1(x)) = x ⇔ aloga x = x. f ( f − 1 ( x)) = x a log a x = x. logarithm, the exponent or power to which a base must be raised to yield a given number. Expressed mathematically, x is the logarithm of n to the base b if bx = n, in which case one writes x = log b n. For example, 2 3 = 8; therefore, 3 is the logarithm of 8 to base 2, or 3 = log 2 8. In the same fashion, since 10 2 = 100, then 2 = log 10 100. Logarithmic Functions. Like many types of functions, the exponential function has an inverse. This inverse is called the logarithmic function. logax = y means ay = x. where a is called the base; a > 0 and a≠1. For example, log232 = 5 because 25 = 32. log5 = - 3 because 5-3 = . To evaluate a logarithmic function, determine what exponent the.
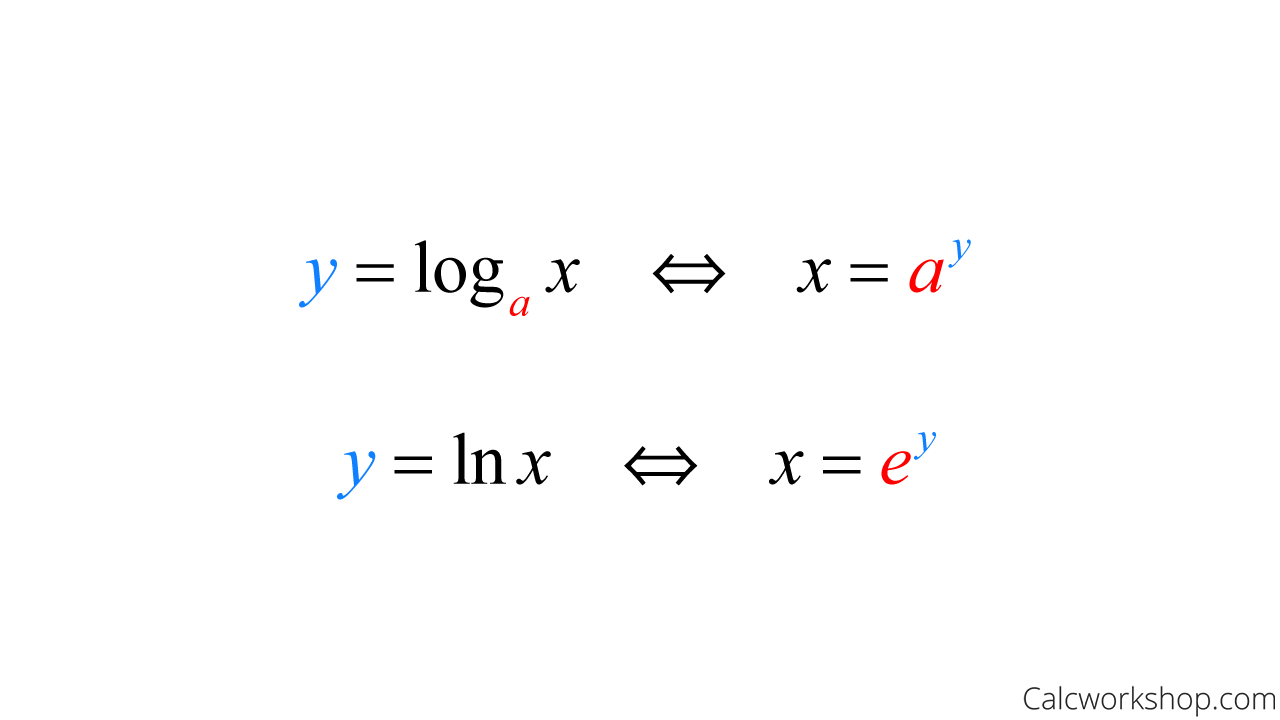
Logarithmic Function Formula
This is the Logarithmic Function: f (x) = log a (x) a is any value greater than 0, except 1 Properties depend on value of "a" When a=1, the graph is not defined Apart from that there are two cases to look at: Plot the graph here (use the "a" slider) In general, the logarithmic function: always has positive x, and never crosses the y-axis k+1) with ∂f(x k+1) = A⊤log Ax k+1 b M k+1 = G(x k+1)−1 with inverse metric tensor as listed in Table1 x k+1 = exp x k (τv k) Increment k←k+ 1. Unlike monotone strategies that strictly ensure a decrease in the sequence of function values (f(x k)) k∈N with each iteration, this approach does not require f(x k+1)
Let's go through the correct application of the logarithmic properties and show why the statement is incorrect: The product rule for logarithms states that log_x (A) + log_x (B) = log_x (A * B). Suppose we have the expressions: (LogX (A) = l) and (LogX (B) = m). According to the product rule, combining these two expressions should give us: Product Formula of logarithms The product formula of logs is, log b (xy) = log b x + log b y. Derivation: Let us assume that log b x = m and log b y = n. Then by the definition of logarithm, x = b m and y = b n. Then xy = b m × b n = b m + n (by a law of exponents, a m × a n = a m + n) Converting xy = b m + n into logarithmic form, we get 
Solving Logarithmic Equations YouTube
Free Logarithms Calculator - Simplify logarithmic expressions using algebraic rules step-by-step What is the Derivative of log x? The derivative of logₐ x (log x with base a) is 1/ (x ln a). Here, the interesting thing is that we have "ln" in the derivative of "log x". Note that "ln" is called the natural logarithm (or) it is a logarithm with base "e". i.e., ln = logₑ.