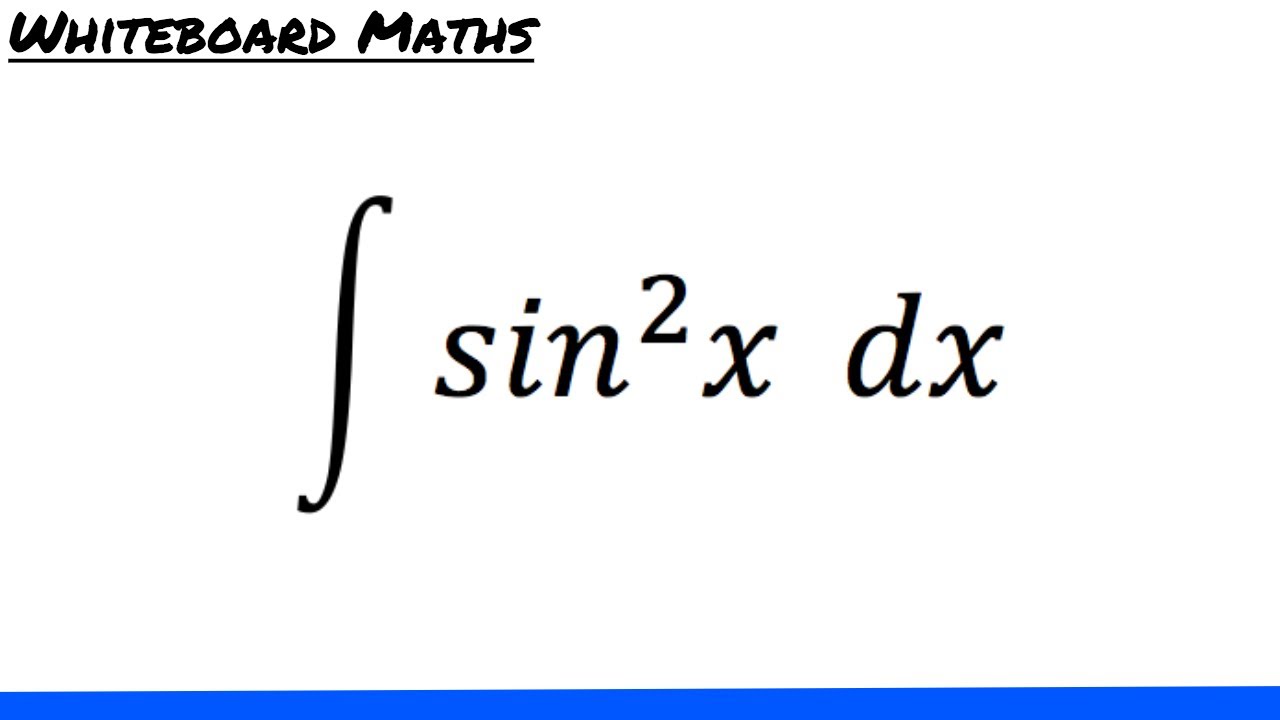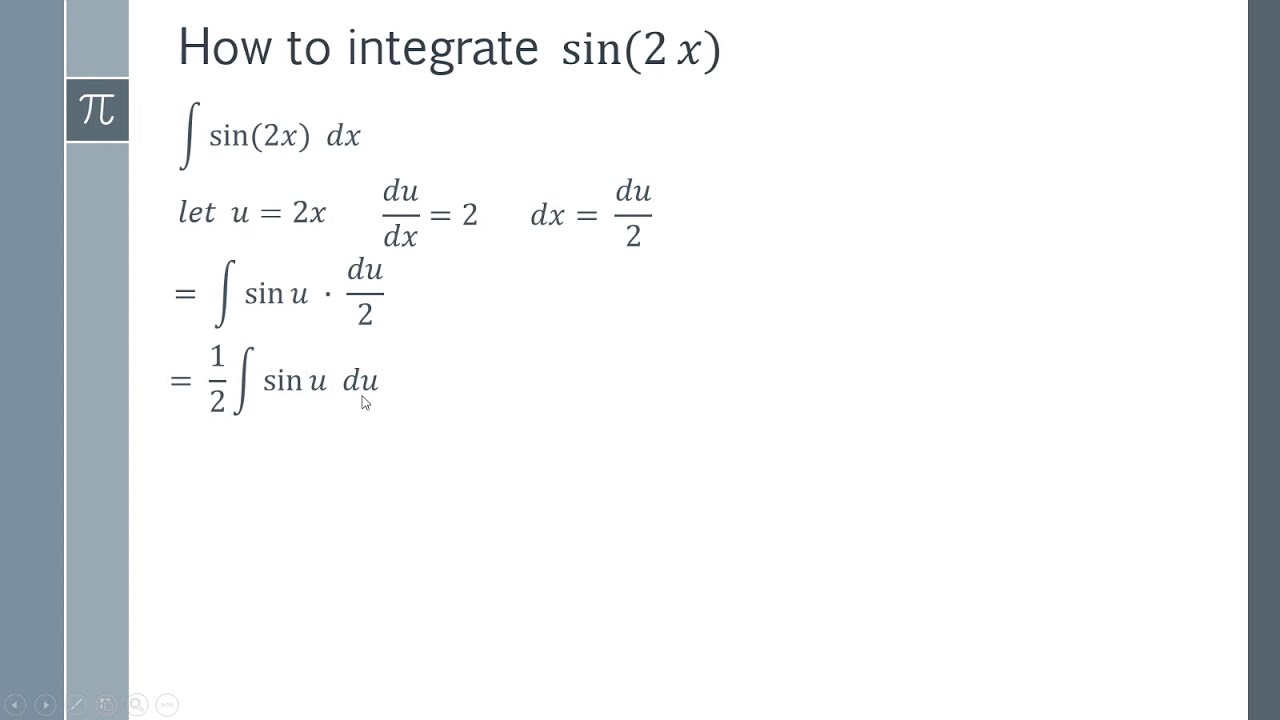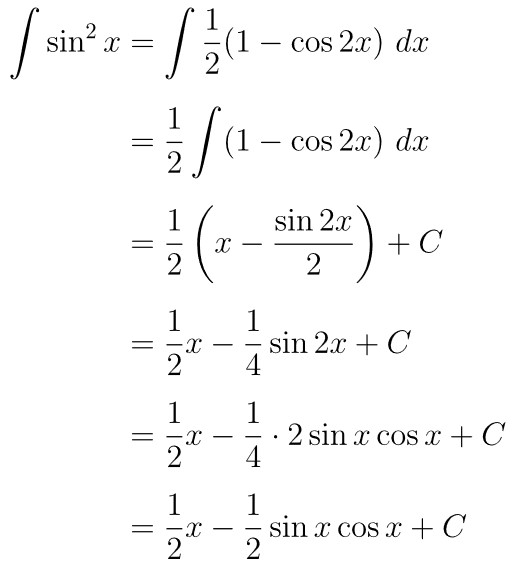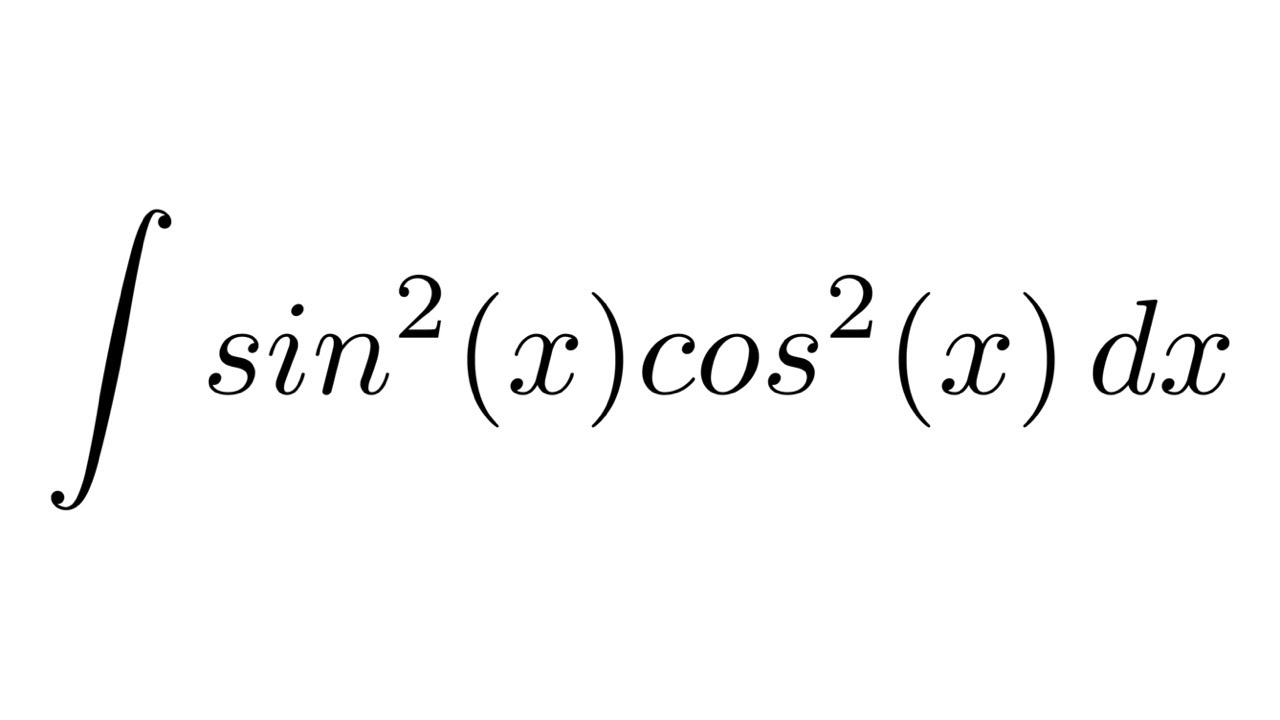Advanced Math Solutions - Integral Calculator, the basics. Integration is the inverse of differentiation. Even though derivatives are fairly straight forward, integrals are. Save to Notebook! Free integral calculator - solve indefinite, definite and multiple integrals with all the steps. Type in any integral to get the solution, steps and. Free Pre-Algebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step
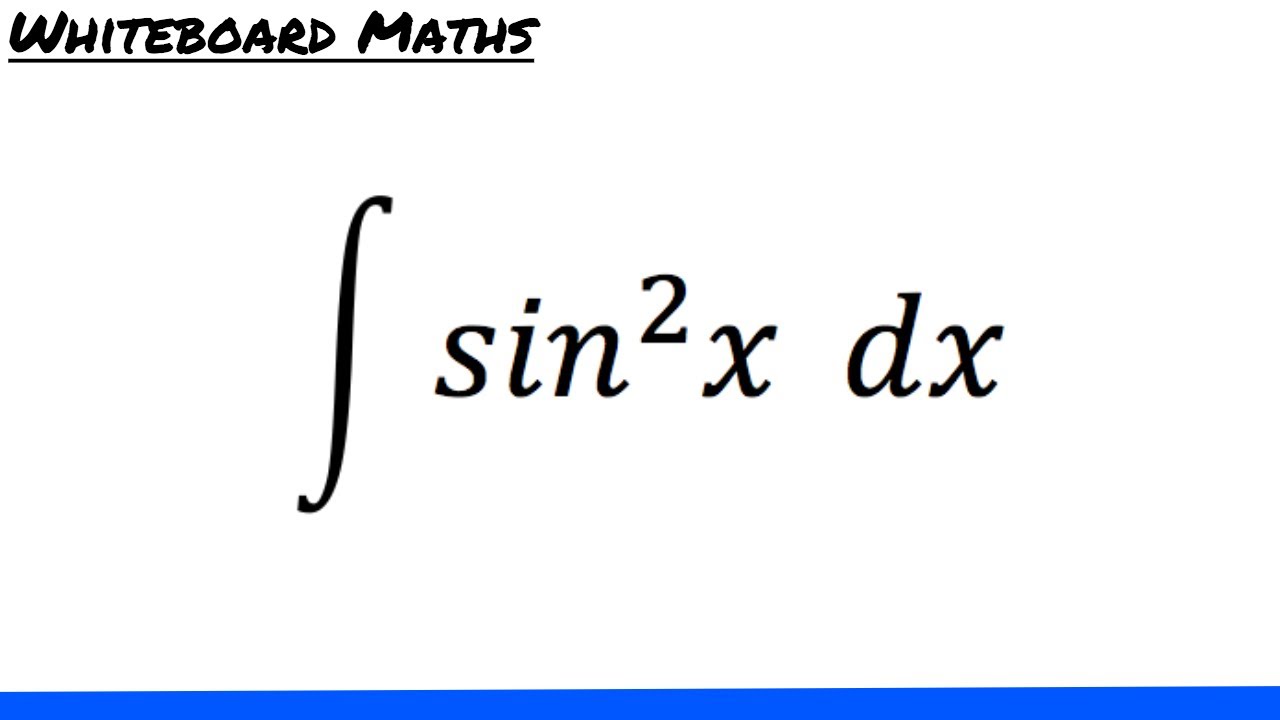
Integral of sin^2 x YouTube
integrate x sin(x^2) integrate x sqrt(1-sqrt(x)) integrate x/(x+1)^3 from 0 to infinity; integrate 1/(cos(x)+2) from 0 to 2pi; integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; View more examples; Access instant learning tools. Get immediate feedback and guidance with step-by-step solutions for integrals and Wolfram Problem Generator. Learn more. Explanation: Now, using the simplified value for sin 2 x, the integral converts to: ∫ sin 2 x = x/2 - (sin 2x)/4 + C [Since the integral of cos ax = sin ax / a] ☛Note: Here, ∫ cos 2x dx value can be computed using integration by substitution. where, C is the constant of integration. For more information, click here. The integral of sin 2x is denoted by ∫ sin 2x dx and its value is - (cos 2x) / 2 + C, where 'C' is the integration constant. For proving this, we use the integration by substitution method. For this, we assume that 2x = u. Then 2 dx = du (or) dx = du/2. Substituting these values in the integral ∫ sin 2x dx, integral of sin^2(x) Natural Language; Math Input; Extended Keyboard Examples Upload Random. Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music…
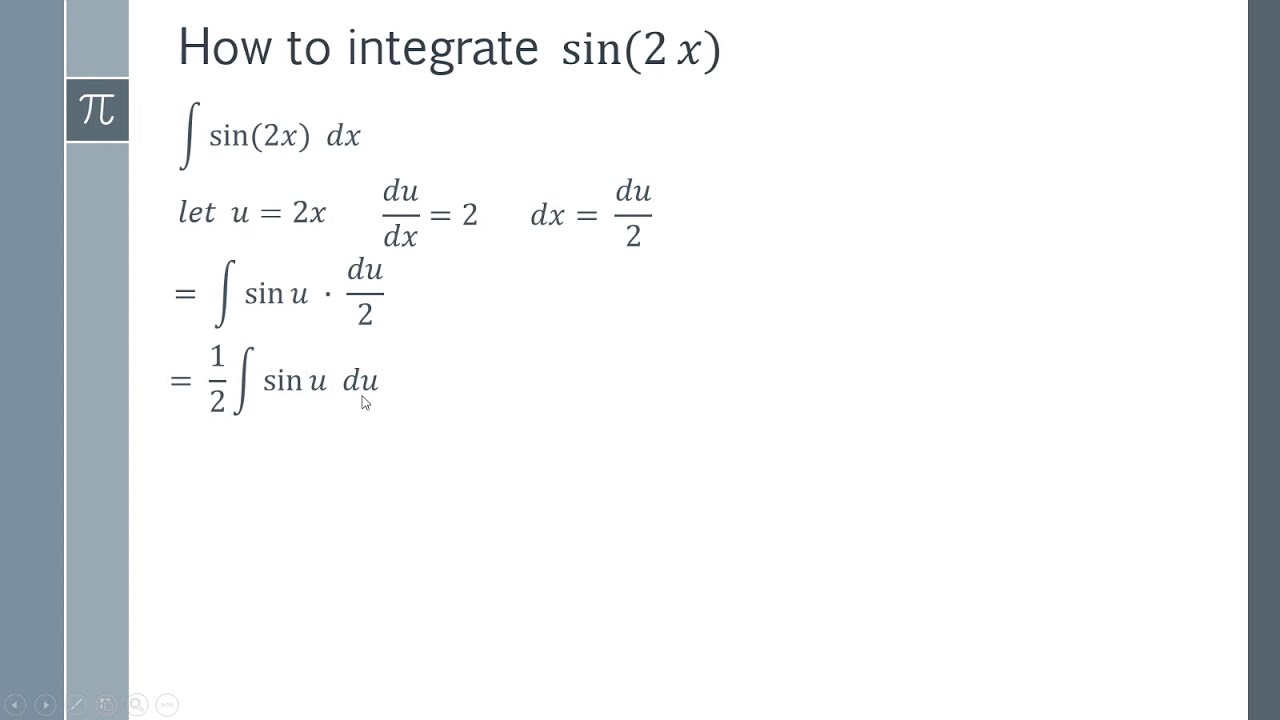
How to Integrate sin 2x Step by Step Integration Proof YouTube
How to integrate sin^2 x using the addition formula for cos(2x) and a trigonometric identity. Case 2: Suppose our integration is of the form. \int \sin^m (x) \cos^n (x)dx, ∫ sinm(x)cosn(x)dx, where m m and n n belong to integers. In this case, we can solve it using u u -substitution: If. m. m m is odd, put. cos ( x) = t. \cos (x) = t cos(x) = t and proceed. If. The cos2(2x) term is another trigonometric integral with an even power, requiring the power--reducing formula again. The cos3(2x) term is a cosine function with an odd power, requiring a substitution as done before. We integrate each in turn below. cos3(2x) = cos2(2x)cos(2x) = (1 − sin2(2x))cos(2x). Equation 1.8.3. cos(2x) = cos2x − sin2x = 2cos2x − 1 = 1 − 2sin2x. Notice that the last two lines of Equation 1.8.3 follow from the first line by replacing either sin2x or cos2x using Equation 1.8.1. It is also useful to rewrite these last two lines:
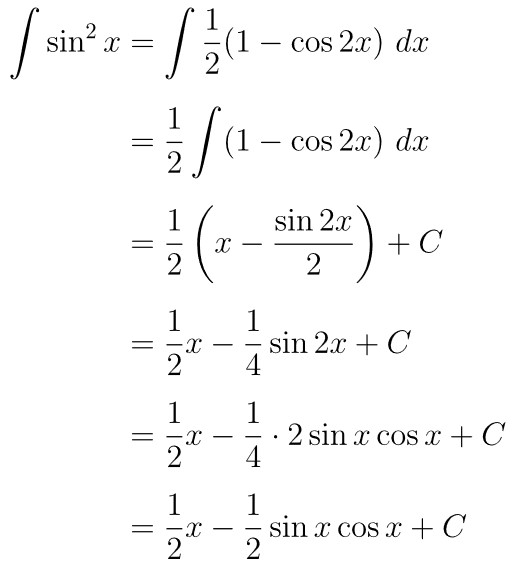
Integral sin^2 x dx Contoh integral trigonometri berpangkat
Integration of Sin 2x Derivation. We can derive the formula of integral of sin2x using the method of integration by substitution. Consider ∫sin2x dx.. \int_{0}^{\frac{\pi}{2}}sin2x\ dx\end{array} \) This is the definite integral of sin2x with lower limit 0 and upper limit π/2. We know that, ∫ sin2x dx = -(½) cos2x + C. First we split sin2(x) = (1−e2ix)+(1−e−2ix) 4 sin 2 ( x) = ( 1 − e 2 i x) + ( 1 − e − 2 i x) 4. To avoid the pole at x = 0 x = 0, drop the path of integration a bit below the real line (this function has no poles and it vanishes at infinity, so this is okay). Next, let γ+ γ + be the path below the real axis, then circling back in.
#intsin^2(x)dx=intfrac{d}{dx}(x)sin^2(x)dx# #=xsin^2(x)-intxfrac{d}{dx}(sin^2(x))dx# #=xsin^2(x)-intx(2sin(x)cos(x))dx# #=xsin^2(x)-intxsin(2x)dx# The cos2(2x) term is another trigonometric integral with an even power, requiring the power--reducing formula again. The cos3(2x) term is a cosine function with an odd power, requiring a substitution as done before. We integrate each in turn below. cos3(2x) = cos2(2x)cos(2x) = (1 − sin2(2x))cos(2x).
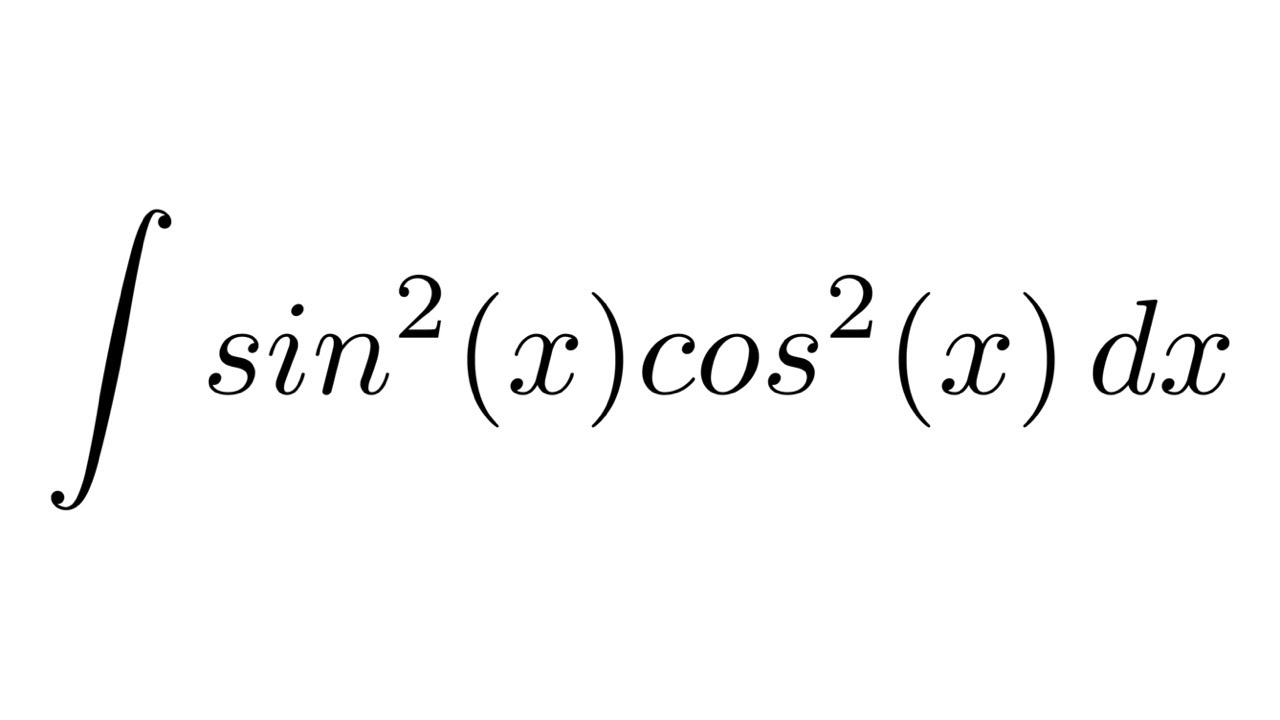
Integral of sin^2(x)cos^2(x) (trigonometric identities) YouTube
As soon as you see a question asking you to integrate the square of sin, cos or tan, your first approach should be to use trigonometric identities and double angle formulas. For sin 2 (X), we will use the cos double angle formula: cos(2X) = 1 - 2sin 2 (X) The above formula can be rearranged to make sin 2 (X) the subject: sin 2 (X) = 1/2(1 - cos(2X)) You can now rewrite the integration: $-\frac{\cos 2x}{2}+C = \int \sin(2x) dx$ Hence the integral of sin2x is -cos 2x/2. Integration of sin2x by using definite integral. The definite integral is a type of integral that calculates the area of a curve by using infinitesimal area elements between two points. The definite integral can be written as: