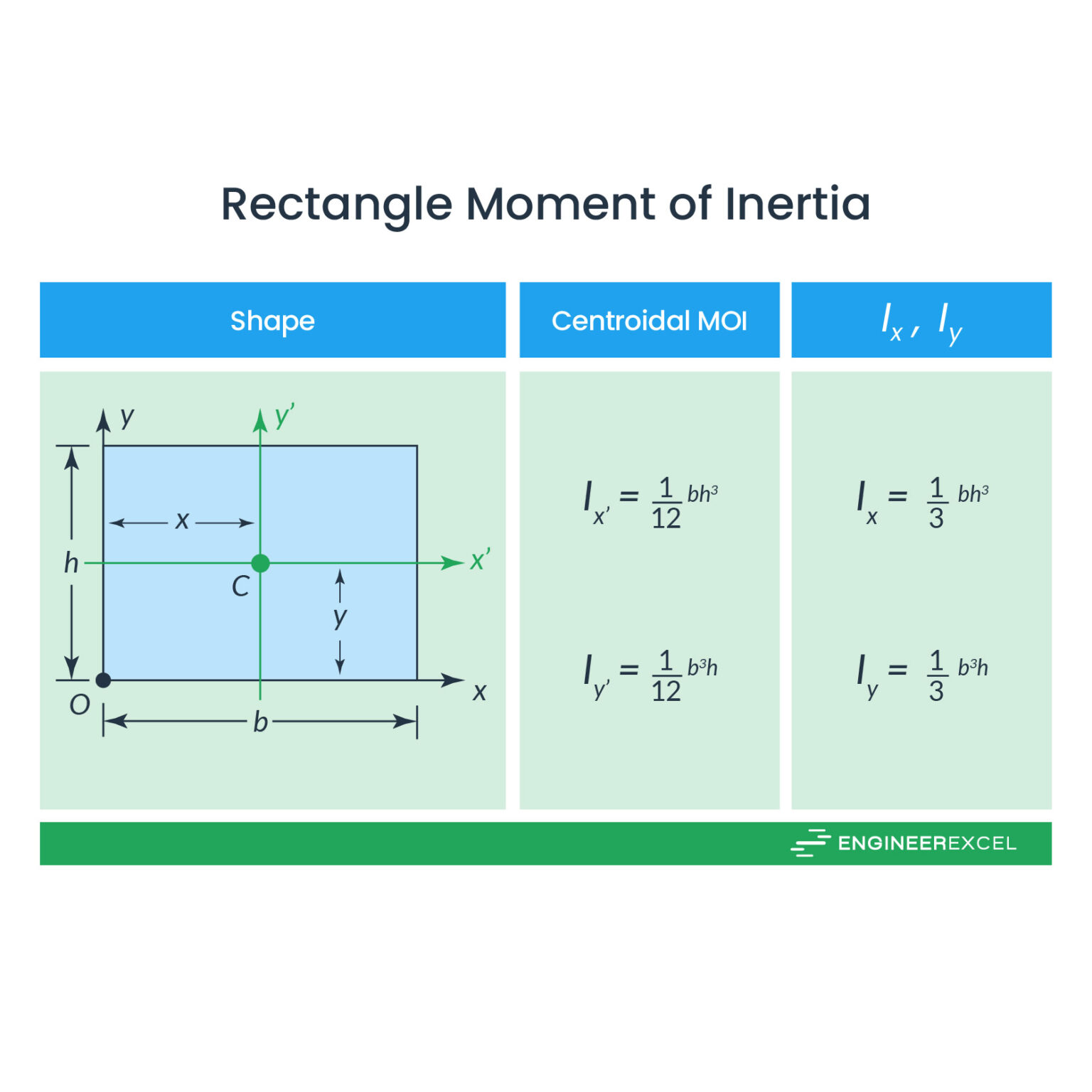
The moment of inertia of a rectangle with respect to an axis passing through its base, is given by the following expression: This can be proved by application of the Parallel Axes Theorem (see below) considering that rectangle centroid is located at a distance equal to h/2 from base. With this result, we can find the rectangular moments of inertia of circles, semi-circles and quarter circle simply. Noting that the polar moment of inertia of a shape is the sum of its rectangular moments of inertia and that \(I_x\) and \(I_y\) are equal for a circle due to its symmetry. Therefore, by (10.5.2), which is easily proven,

Moment of Inertia Formula, Definition, Equations, Units, Examples
In summary, the formula for determining the moment of inertia of a rectangle is Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. For rectangular hollow sections, the formula is Ixx=BD³ ⁄ 12 - bd³ ⁄ 12. The moment inertia is important for both bending moment force/stress and deflection. When we take a situation when the axis passes through the centroid, the moment of inertia of a rectangle is given as: I = bh 3 / 12 Here, b is used to denote the rectangle width (the dimension parallel to the axis) and h is said to be the height (dimension perpendicular to the axis). 2. An Axis Passing Through Its Base Moment of inertia, denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, it is the rotational analogue to mass (which determines an object's resistance to linear acceleration ). The moments of inertia of a mass have units of dimension ML 2 ( [mass] × [length] 2 ). Fundamentally, the moment of inertia is the second moment of area, which can be expressed as the following: Ix = ∫ ∫y2dA I x = ∫ ∫ y 2 d A. Iy = ∫ ∫x2dA I y = ∫ ∫ x 2 d A. To observe the derivation of the formulas below, we try to find the moment of inertia of an object such as a rectangle about its major axis using just the.
Parallel Axis Theorem for Area Moment of Inertia EngineerExcel
Moment of inertia is the property of a deformable body that determines the moment needed to obtain a desired curvature about an axis. Moment of inertia depends on the shape of the body and may be different around different axes of rotation. Moment-curvature relation: E: Elasticity modulus (characterizes stiffness of the deformable body) : curvature To calculate the moment of inertia of a rectangle, you can use the formula: I = (b * h^3) / 12. I is the moment of inertia of the rectangle b is the width of the rectangle h is the height of the rectangle. It is important to note that the unit of measurement for b and h must be consistent (e.g., inches, millimeters, etc.). When the moment of inertia is calculated about two orthogonal axes in the plane of the area, it is called the rectangular moment of inertia. If x and y are two perpendicular axes (Fig. 10.2), the moments of inertia of an area about the x and y axes are denoted as and and determined by, (10.2) Moment of Inertia of Rectangle Definition The rectangle's moment of inertia is defined as: The summation of products is obtained from the entire mass of every attached element of the rectangle and then multiplied the value by the square of the particles with respect to its distance from the central point.
Moment Of Inertia Of Rectangle Engineering Mechanics Civil Stuff YouTube
See also: Moment of Inertia--Rectangular Parallelepiped, Routh's Rule . Mechanics: Angular Momentum: Moment of Inertia--Rectangle : Consider an ellipse of mass M and semiaxes lengths a and b. The surface density is then (1) and the moment of inertia tensor is (2) (3) Moment of Inertia--Rectangular Parallelepiped, Routh's Rule The moment of inertia is defined as the product of mass of section and the square of the distance between the reference axis and the centroid of the section. Spinning figure skaters can reduce their moment of inertia by pulling in their arms, allowing them to spin faster due to conservation of angular momentum.
I parallel-axis = 1 2 m d R 2 + m d ( L + R) 2. Adding the moment of inertia of the rod plus the moment of inertia of the disk with a shifted axis of rotation, we find the moment of inertia for the compound object to be. Itotal = 1 3mrL2 + 1 2mdR2 + md(L + R)2. I total = 1 3 m r L 2 + 1 2 m d R 2 + m d ( L + R) 2. The moment of inertia of a rectangle has been expressed as follows when an axis passes through the base: I = bh3 / 3 It is seamlessly determined by applying the Parallel Axis Theorem because the rectangle centroid is located at a distance equal to h/2 from the base. Parallel Axis Theorem

CE1103Moment of inertia for the rectangle sectionStaticsEnglish. YouTube
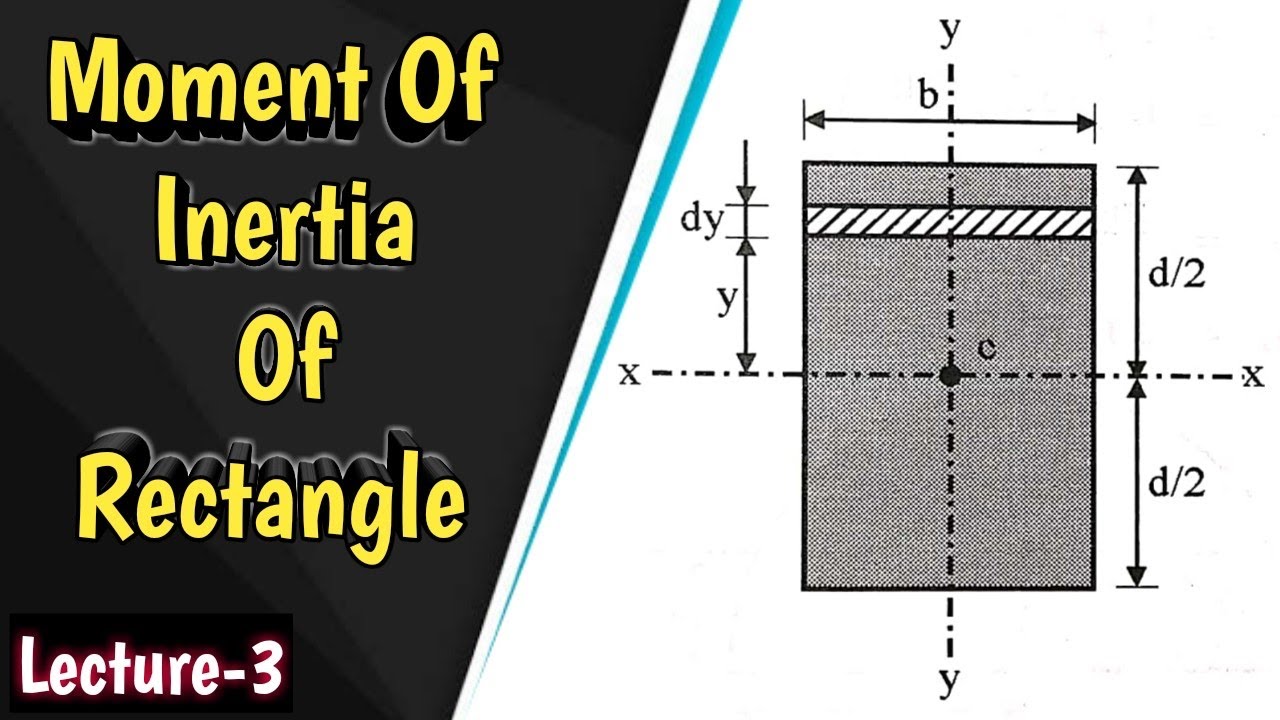
Moment of Inertia of a Rectangle. Example 10.3.7. Interactive: Semi-Circle. Use this interactive to practice computing the area moments of inertia of the semi-circle about the centroidal \(x'\) axis, the bottom edge \(x''\text{,}\) and the system \(x\) axis. You can change the location and size of the semicircle by moving the red points.. 2 Answers Sorted by: 7 You have misunderstood the parallel axis theorem. The moment of inertia of an object around an axis is equal to I = ∬ R ρ2dA where ρ is the distance from any given point to the axis. In the case of a rectangular section around its horizontal axis, this can be transformed into




