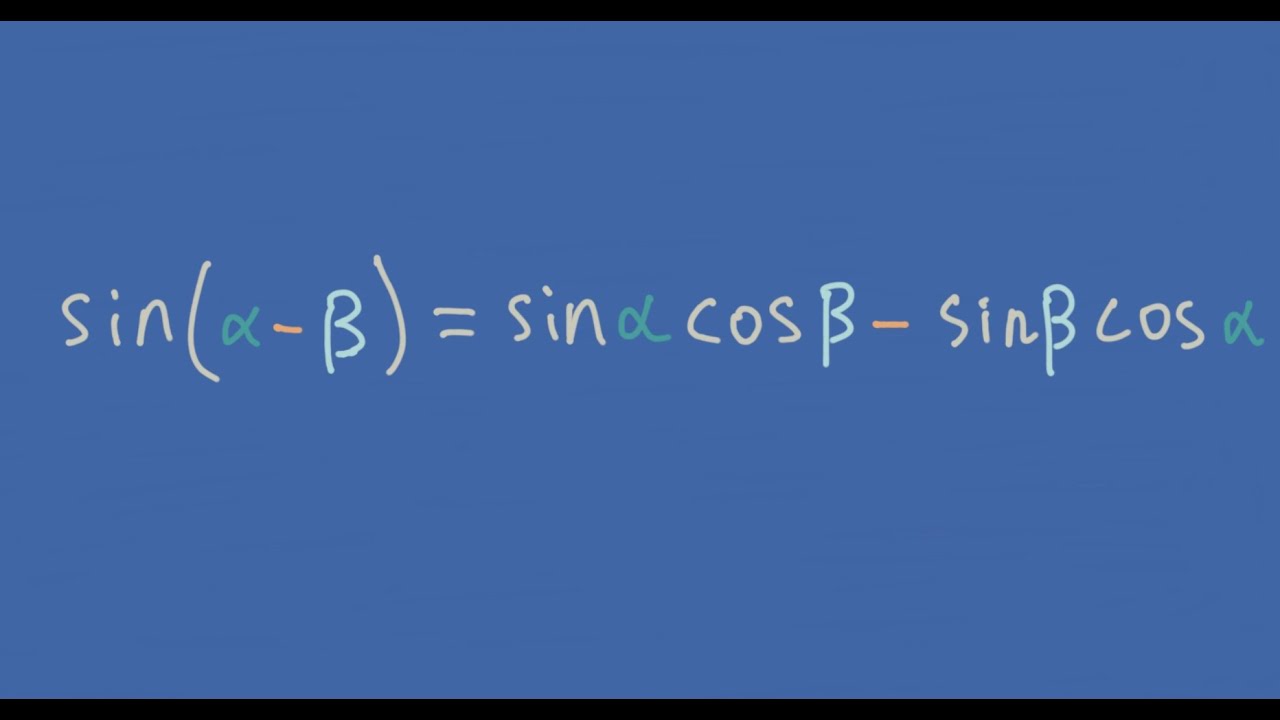The basic relationship between the sine and cosine is given by the Pythagorean identity: where means and means This can be viewed as a version of the Pythagorean theorem, and follows from the equation for the unit circle. Mathematical form The sine of difference of two angles formula can be written in several ways, for example sin ( A − B), sin ( x − y), sin ( α − β), and so on but it is popularly written in the following three mathematical forms. ( 1) sin ( A − B) = sin A cos B − cos A sin B ( 2) sin ( x − y) = sin x cos y − cos x sin y

Visual proof of sin(A+B) formula YouTube
Sin (a + b) is one of the important trigonometric identities used in trigonometry. It is one of sum and difference formulas. It says sin (a + b) = sin a cos b + cos a sin b. We use the sin (a + b) identity to find the value of the sine trigonometric function for the sum of angles. Sin (a - b) is one of the important trigonometric identities used in trigonometry, also called sin (a - b) compound angle formula. Sin (a - b) identity is used in finding the value of the sine trigonometric function for the difference of given angles, say 'a' and 'b'. Sin A - Sin B is an important trigonometric identity in trigonometry. It is used to find the difference of values of sine function for angles A and B. It is one of the difference to product formulas used to represent the difference of sine function for angles A and B into their product form. Free trigonometry calculator - calculate trignometric equations, prove identities and evaluate functions step-by-step

How to Use the Sine Rule 11 Steps wikiHow
The Trigonometric Identities are equations that are true for Right Angled Triangles. (If it is not a Right Angled Triangle go to the Triangle Identities page.) Each side of a right triangle has a name: Adjacent is always next to the angle And Opposite is opposite the angle 1 4 involving products of sines and cosines now add equation (2) to equation (7) sin(A − B) +(sin(A + B) = sin A cos B − cos A sin B = sin A cos B + cos A sin B) we find sin(A − B) + sin(A + B) = 2 sin A cos B and dividing both sides by 2 we obtain the identity 1 1 sin A cos B = sin(A − B) + sin(A + B). 2 2 3/1. 4/0. Given Triangle abc, with angles A,B,C; a is opposite to A, b opposite B, c opposite C: a/sin (A) = b/sin (B) = c/sin (C) (Law of Sines) c ^2 = a ^2 + b ^2 - 2ab cos (C) b ^2 = a ^2 + c ^2 - 2ac cos (B) a ^2 = b ^2 + c ^2 - 2bc cos (A) (Law of Cosines) The Law of Sines The Law of Sines (or Sine Rule) is very useful for solving triangles: a sin A = b sin B = c sin C It works for any triangle: And it says that: When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B, and also equal to side c divided by the sine of angle C Sure. ?
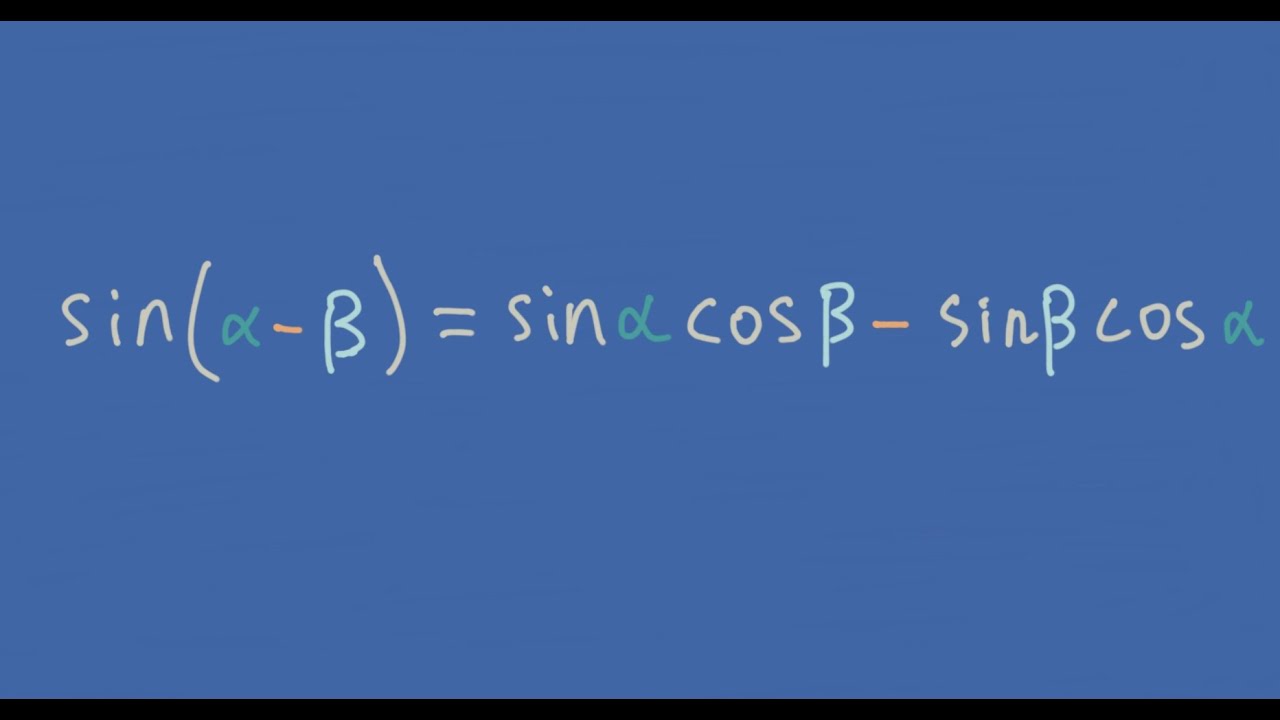
sin(ab) Formula DERIVED YouTube
Sum and product formulae cosA+ cosB= 2cos A+ B 2 cos A B 2 (13) cosA cosB= 2sin A+ B 2 sin A B 2 (14) sinA+ sinB= 2sin A+ B 2 cos A B 2 (15) sinA sinB= 2cos A+ B 2 sin A B 2 (16) Note that (13) and (14) come from (4) and (5) (to get (13), use (4) to expand cosA= cos(A+ B 2+2) and (5) to expand cosB= cos( A+B 2 2), and add the results). Sin (A + B) is the two parts of the opposite - all divided by the hypotenuse (9). Putting that into its trig form: sin (A + B) = sin A cos B + cos A sin B
The following (particularly the first of the three below) are called "Pythagorean" identities. sin 2 ( t) + cos 2 ( t) = 1. tan 2 ( t) + 1 = sec 2 ( t) 1 + cot 2 ( t) = csc 2 ( t) Advertisement. Note that the three identities above all involve squaring and the number 1. You can see the Pythagorean-Thereom relationship clearly if you consider. Part of Maths Geometry and measure The sine rule - Higher The angles are labelled with capital letters. The opposite sides are labelled with lower case letters. Notice that an angle and its.

Даю 50 баллов!!!! Помоги Алгебра.упростите выраженияsin (aB) + 2 cos a×sin B Школьные
Proving Trigonometric Identities - Basic. Trigonometric identities are equalities involving trigonometric functions. An example of a trigonometric identity is. \sin^2 \theta + \cos^2 \theta = 1. sin2 θ+cos2 θ = 1. In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identities. In this post, we will establish the formula of sin (a+b) sin (a-b). Note that sin (a+b) sin (a-b) is a product of two sine functions. We will use the following two formulas: sin (a+b) = sin a cos b + cos a sin b. (i) sin (a-b) = sin a cos b - cos a sin b. (ii) Table of Contents Formula of sin (a+b) sin (a-b) sin (a+b) sin (a-b) Formula: