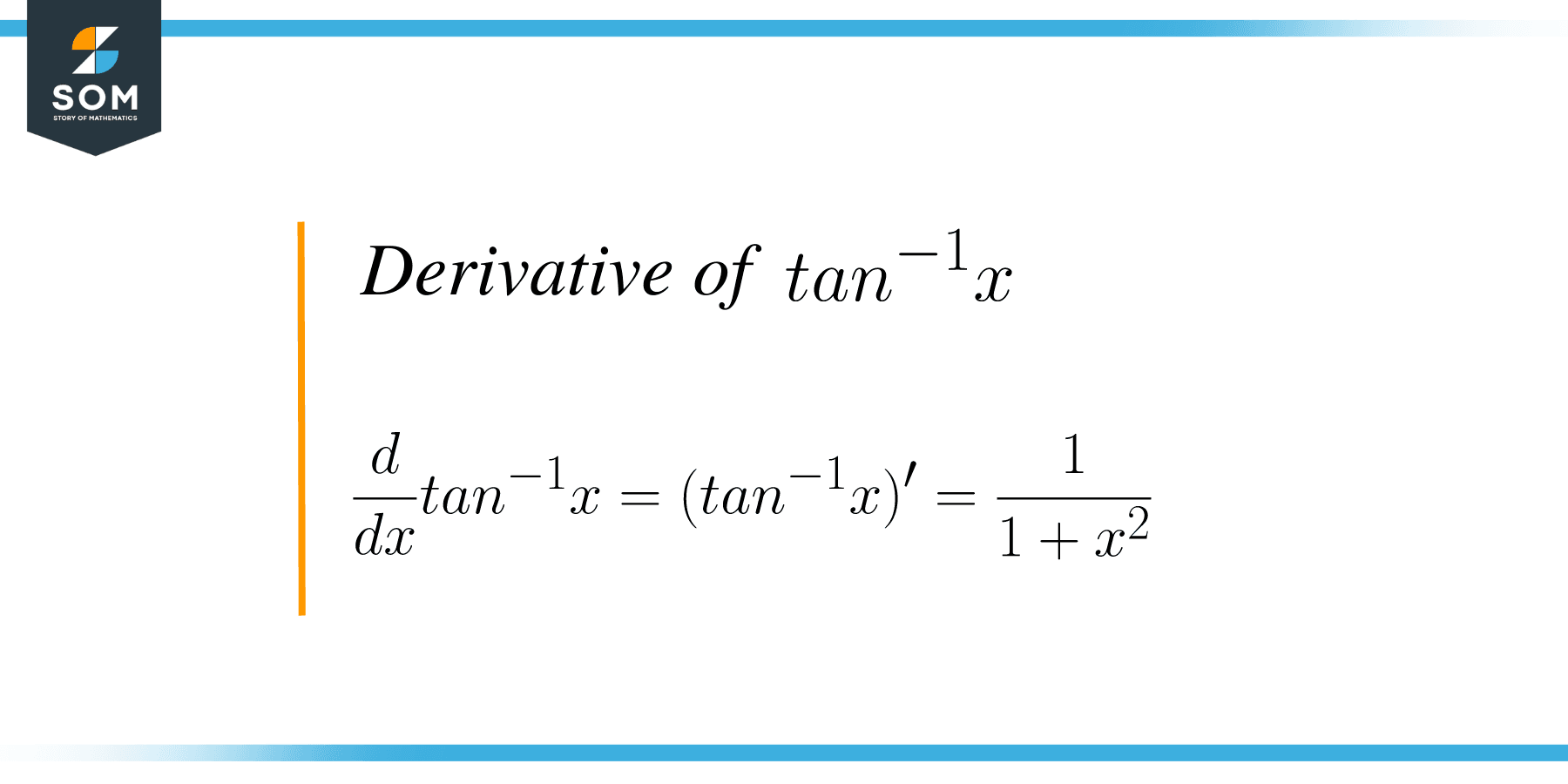Free derivative calculator - differentiate functions with all the steps. Type in any function derivative to get the solution, steps and graph Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2 ). The derivative of tan inverse x can be calculated using different methods such as the first principle of derivatives and using implicit differentiation.

Derivative of Tan Differentiation & Formula Video & Lesson Transcript
1 Answer Truong-Son N. Jul 1, 2015 I seem to recall my professor forgetting how to deriving this. This is what I showed him: y = arctanx tany = x sec2y dy dx = 1 dy dx = 1 sec2y Since tany = x 1 and √12 +x2 = √1 +x2, sec2y = ( √1 + x2 1)2 = 1 + x2 ⇒ dy dx = 1 1 + x2 I think he originally intended to do this: dy dx = 1 sec2y sec2y = 1 + tan2y Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier. (tan^{-1}x\right) en. Related Symbolab blog posts. Practice Makes Perfect. Learning math takes practice, lots of practice. Just like running, it takes practice. 1 It boils down to: what do you mean by $\tan^ {-1} (x)$. I think most people think of it as the inverse tangent function, i.e. $\arctan (x)$, but some think of it as $\frac {1} {\tan (x)}$. The derivative of the former is $\frac {1} {1+x^2}$, and the derivative of $\tan (x)$ is $\sec^2 (x)$. The differentiation of the tan inverse function can be written in terms of any variable. Here are some of the examples to learn how to express the formula for the derivative of inverse tangent function in calculus. ( 1) d d y ( tan − 1 ( y)) = 1 1 + y 2 ( 2) d d l ( tan − 1 ( l)) = 1 1 + l 2 ( 3) d d z ( tan − 1 ( z)) = 1 1 + z 2 Proof

Derivative of Tangent x Formula, Rules, Examples
[Math Processing Error] Answer link I'm assuming you are thinking of this as being a function of two independent variables x and y: z=tan^ {-1} (y/x). The answers are \frac {\partial z} {\partial x}=-\frac {y} {x^ {2}+y^ {2}} and \frac {\partial z} {\partial y}=\frac {x} {x^2+y^2}. What Is the Derivative of Tan^-1 x? The derivative of t a n − 1 x or arc tan (x) is the process of differentiating the arc tan trigonometric function with respect to "x". Tangent is a trigonometric function, and if we take the inverse of this function, then it is called the inverse tangent function or arc tan function. Since tan y=x, the tan ratio opposite/adjacent tells you that your opposite side is x and adjacent side is 1. Now use pythagorean theorem to find the hypoteneuse, which is sqrt (x^2+1). Then form cos y= 1/sqrt (x^2+1) and sub. it back into the above formula, squaring it to give you 1/ (1+x^2). •. 1 Answer Jim H Aug 4, 2015 Use the derivative of tan−1 and the chain rule. Explanation: The derivative of tan−1x is 1 1 +x2 (for "why", see note below) So, applying the chain rule, we get: d dx (tan−1u) = 1 1 +u2 ⋅ du dx In this question u = 2x, so we get: d dx (tan−12x) = 1 1 +(2x)2 ⋅ d dx (2x) = 2 1 + 4x2 Note If y = tan−1x, then tany = x
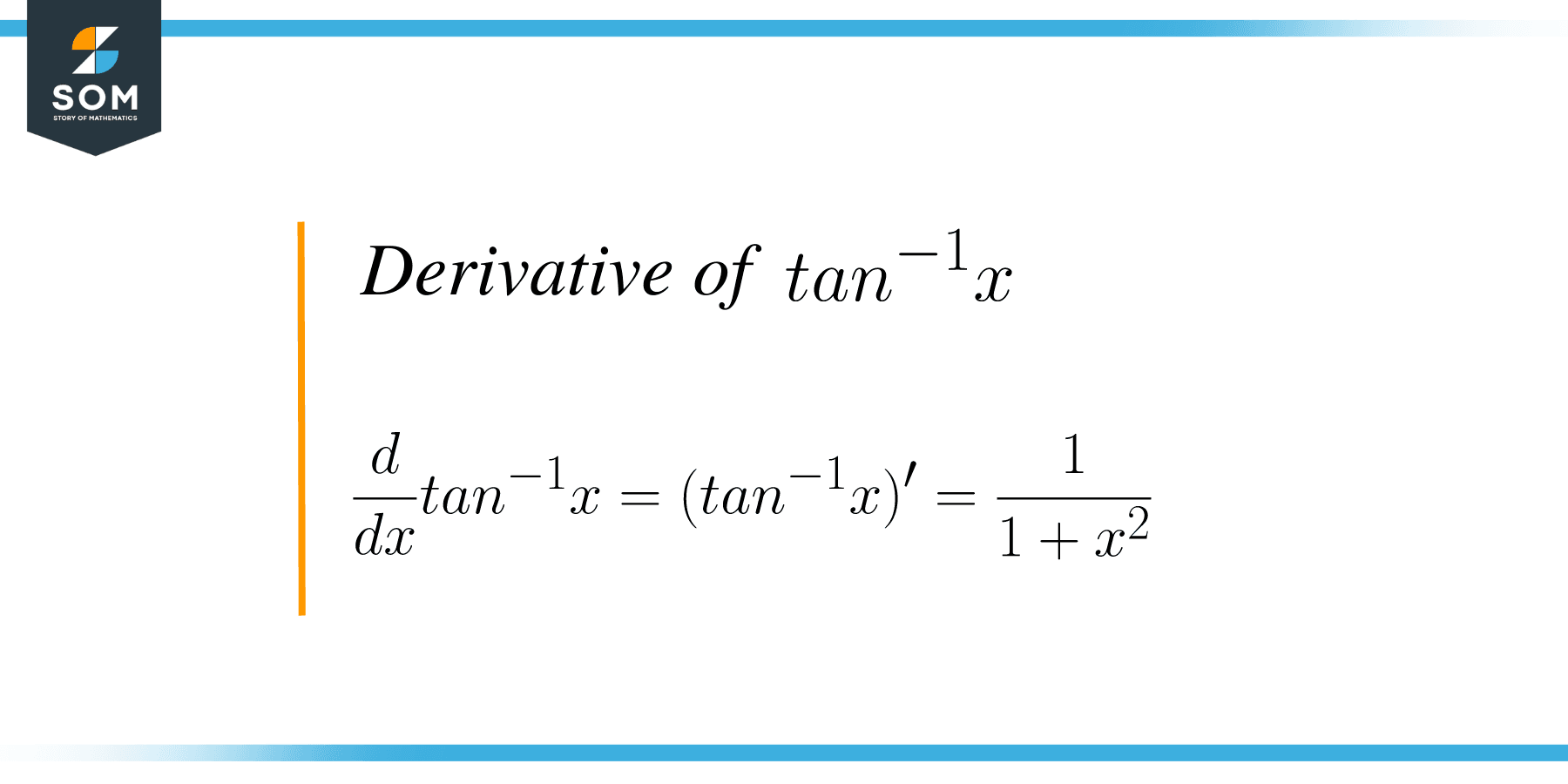
Derivative of Tan^1 x Detailed Explanation and Examples The Story of Mathematics A History
The differentiation of t a n − 1 x with respect to x is 1 1 + x 2. i.e. d d x t a n − 1 x = 1 1 + x 2. Proof using chain rule : Let y = t a n − 1 x. Then, t a n ( t a n − 1 x) = x tan y = x Differentiating both sides with respect to x, we get d d x (tan y) = d d x (x) d d x (tan y) = 1 By chain rule, s e c 2 y d y d x = 1 d y d x = 1 s e c 2 y Thus we have found the derivative of y = arcsin x, (6) d d x ( arcsin x) = 1 1 − x 2. Exercise 1. Use the same approach to determine the derivatives of y = arccos x, y = arctan x, and y = arccot x. Answer. Example 2: Finding the derivative of y = arcsec x. Find the derivative of y = arcsec x.
Here is a list of the derivatives that you need to know: d (sin x) = cos x dx. d (cos x) = -sin x dx. d (sec x) = sec x tan x dx. d (cosec x) = -cosec x cot x dx. d (tan x) = sec²x dx. d (cot x) = -cosec²x dx. One condition upon these results is that x must be measured in radians. Applying the Chain Rule Example 3.5.2: Finding the Derivative of a Function Containing cos x. Find the derivative of g(x) = cosx 4x2. Solution. By applying the quotient rule, we have. g′ (x) = ( − sinx)4x2 − 8x(cosx) (4x2)2. Simplifying, we obtain. g′ (x) = − 4x2sinx − 8xcosx 16x4 = − xsinx − 2cosx 4x3.

Differentiation of tan inverse x is ? Brainly.in
How Wolfram|Alpha calculates derivatives. Wolfram|Alpha calls Wolfram Languages's D function, which uses a table of identities much larger than one would find in a standard calculus textbook. It uses well-known rules such as the linearity of the derivative, product rule, power rule, chain rule and so on. Additionally, D uses lesser-known rules. All derivatives of circular trigonometric functions can be found from those of sin ( x) and cos ( x) by means of the quotient rule applied to functions such as tan ( x) = sin ( x )/cos ( x ). Knowing these derivatives, the derivatives of the inverse trigonometric functions are found using implicit differentiation .