The unit circle with tangent is also known as the trigonometric circle of the tangent function. It gives the values of the trigonometric function "tan" for different standard angles that lie between 0° and 360°. The standard angles between 0° and 360° are tabulated below both in terms of degrees and radians. Unit circle Google Classroom About Transcript Learn how to use the unit circle to define sine, cosine, and tangent for all real numbers. Created by Sal Khan. Questions Tips & Thanks Sort by: Top Voted Vamsavardan Vemuru 11 years ago Do these ratios hold good only for unit circle? What if we were to take a circles of different radii? • 2 comments
Tan 30 Degrees Value (Unit Circle Tangent Value)
Unit test About this unit Discover how to measure angles, distances, and heights using trigonometric ratios and the unit circle. Learn how to use sine, cosine, and tangent to solve real-world problems involving triangles and circular motion. Unit circle introduction Learn Unit circle The trig functions & right triangle trig ratios Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: For a given angle θ each ratio stays the same no matter how big or small the triangle is Trigonometry Index Unit Circle TL;DR Unit circle relations for sine and cosine: Sine is the y-coordinate; and Cosine is the x-coordinate 🙋 Do you need an introduction to sine and cosine? Visit our sine calculator and cosine calculator! Standard explanation: Let's take any point A on the unit circle's circumference. The coordinates of this point are Answer. A unit circle is a circle that is centered at the origin and has radius 1, as shown below. If (x, y) are the coordinates of a point on the circle, then you can see from the right triangle in the drawing and the Pythagorean Theorem that x2 + y2 = 1. This is the equation of the unit circle.
How to Use the Unit Circle in Trigonometry HowStuffWorks
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) [1] [2] are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. Unit circle with cos, sin and tan. Save Copy. Log InorSign Up. This animation shows the unit circle and the value of three trigonometric functions in terms of the angle "a" in radians. 1. y 2 + x 2. On the unit circle, tan (θ) is the length of the line segment formed by the intersection of the line x=1 and the ray formed by the terminal side of the angle as shown in blue in the figure above. This trigonometry tutorial video explains the unit circle and the basics of how to memorize it. It provides the angles in radians and degrees and shows you.

Unit Circle Quick Lesson Printable PDF Chart · Matter of Math
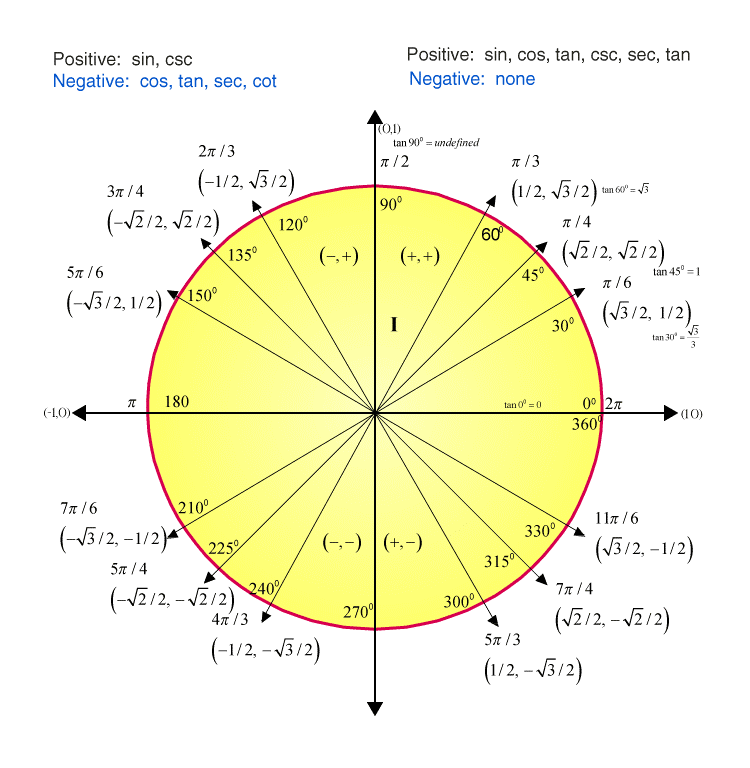
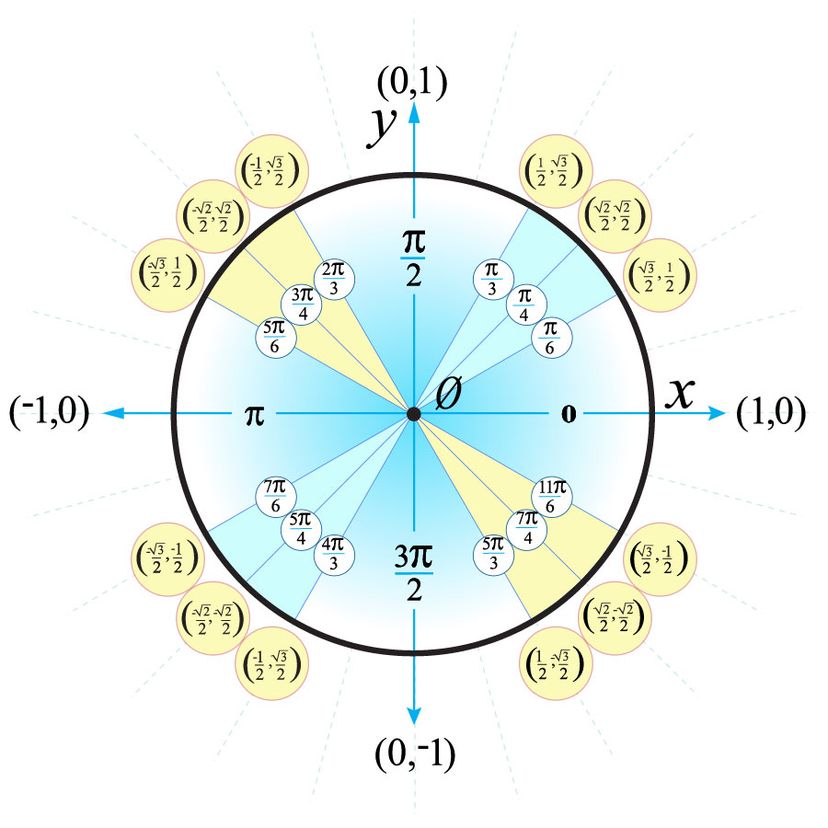
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:tri. Unit Circle Trigonometry Drawing Angles in Standard Position UNIT CIRCLE TRIGONOMETRY The Unit Circle is the circle centered at the origin with radius 1 unit (hence, the "unit" circle). The equation of this circle is xy22+ =1. A diagram of the unit circle is shown. tan() y x θ= ()x ≠0 () 1 cot tan x y
1: The Trigonometric Functions The unit circle is a circle centered on the origin with a unit radius, 1. Sine, Cosine, Tangent The measurements of sin, cos, and tan become clear when you see them on a graph. Take a moment to soak in what they mean. Sin, Cos, Tan at 0° So, what are the sin, cos, and tan of an angle of 0°? Sin, Cos, Tan at 90° And what about 90°?

Unit Circle Quick Lesson Printable PDF Chart · Matter of Math
The "Unit Circle" is a circle with a radius of 1. Being so simple, it is a great way to learn and talk about lengths and angles. The center is put on a graph where the x axis and y axis cross, so we get this neat arrangement here. Sine, Cosine and Tangent Because the radius is 1, we can directly measure sine, cosine and tangent. The relationships between the graphs (in rectangular coordinates) of sin(x), cos(x) and tan(x) and the coordinates of a point on a unit circle are explored using an applet. Definitions 1- Let x be a real number and P(x) a point on a unit circle such that the angle in standard position whose terminal side is segment OP is equal to x radians.(O is the origin of the system of axis used).




