Zijde AC is de overstaande rechthoekszijde van (hoek) ∠B. Zijde AB is de aanliggende rechthoekszijde van ∠B. Met de tangens kun je de zijden en hoeken berekenen in een rechthoekige driehoek. In een niet-rechthoekige driehoek gelden er andere goniometrische regels, zoals de sinus- en cosinus regel. De tangens is altijd de uitkomst van een. Er zijn verschillende mogelijkheden om een hoek te berekenen. In dit voorbeeld gaan we uit van een rechthoekige driehoek en berekenen we de hoek aan de hand van sinus formule. Formule: sin ∠ = overstaande zijde / schuine zijde. We kijken naar bovenstaand voorbeeld. ∠C = hier de hoek van 90 graden.

hoek berekenen met de tangens YouTube
Door het been tegenover de hoek te delen door de catheth die een van de zijden van de hoek is, wordt de tangenswaarde verkregen die overeenkomt met een bepaalde graadmaat. Tangens. Hoe de raaklijn te berekenen ? Laat ABC een rechthoekige driehoek zijn op C en op de hoek op A. tan(a) = tegenoverliggende zijde / aangrenzende zijde = BC / AC goniometrische functie » tangens Tangensfunctie. Funtion tangens is gedefinieerd als de verhouding van de rechthoekige driehoek tegenover en aangrenzende zijde. De functie wordt gedefinieerd in het traject van 90 ° ± k · 180 ° tot 270 ° ± k · 180 ° en neemt waarden uit −∞ tot +∞. Ga nu naar http://www.WiskundeAcademie.nl voor nog meer online gratis video uitleg over alle onderwerpen van wiskunde op de middelbare school!Volg ons op twi. Slagen voor je examen? Check: https://www.mathwithmenno.nl/Volg Math with Menno op Instagram: https://www.instagram.com/mathwithmenno/?hl=nl Blij met mijn vi.

06. Zijde berekenen met tangens (Serie goniometrie) YouTube
Video met uitleg over hoe je bepaalt welke formule je nodig hebt om een hoek in een rechthoekige driehoek uit te rekenen. Gebruik je sinus, cosinus of tangen. In deze theorie leggen we je de basis uit van hoe je met de sinus, cosinus en tangens kunt werken om zo elke scherpe hoek van een rechthoekige driehoek te kunnen berekenen. Methode. De sinus, cosinus en tangens geven allen de verhouding aan tussen twee zijden van een rechthoekige driehoek. Tangens. Dat tangens een breuk is heeft belangrijke gevolgen voor de grafiek van y = tan x. Immers als de noemer van een breuk nul is, dan bestaat die breuk niet, en dat geeft in de grafiek een verticale asymptoot. Dus op de plaatsen waar cos x = 0 zal de grafiek van tan x een asymptoot hebben. Dat is bij x = 1 / 2 π en x = 1 1 / 2 π (en. Berekenen van een percentage van een getal, wijzigen van een getal met een percentage:. De cosinus van de hoek berekenen: cos 1 8 0 = −1: tan: De tangens van de hoek berekenen: tan 4 5 = 1: cot: De cotangens van de hoek berekenen: cot 9 0 = 0: sec csc: Berekenen van de secans van de hoek en de cosecans van de hoek: sec 6 0 = 2: sinh cosh.

Hoeken berekenen met de tangens (3 HAVO & 3 VWO) YouTube
Maak een schets als deze nog niet gegeven is. 2. Schrijf de regel voor de tangens op. Gebruik indien nodig 2 = 6 3. Voorbeeld 1: Hoek berekenen. Vraag: Bereken A op één decimaal nauwkeurig. Antwoord: 2. tan(A) = o a 3. tan(A) = 10 3 4. A = tan-1 (10 3. Bereken de lengte van AC op één decimaal nauwkeurig. Antwoord: 1. Maak eerst een. Bereken de tangens van een gegeven hoek in graden of radialen. berekening.net. Berekening.net / Wiskundige rekenmachines / Tangens rekenmachine. Tangens rekenmachine.
Als je de tangens van een hoek hebt berekend, kan je de hoek berekenen met: shift tan (getal) = hoek. Drieletternotatie van een hoek. De middelste letter geeft de hoek aan, de andere letters de driehoek. ∠ADC betekent. Slide 21-Quizvraag. zijde berekenen als de hoek bekend is. C. A. B. Methode. De formule die we kennen om met behulp van de tangens een hoek te berekenen, is als volgt: tan(∠A) = overstaande rechthoekszijde van ∠A aanliggende rechthoekszijde van ∠A tan ( ∠ A) = overstaande rechthoekszijde van ∠ A aanliggende rechthoekszijde van ∠ A. Als je nu deze formule omschrijft zodat een van de zijden alleen aan.
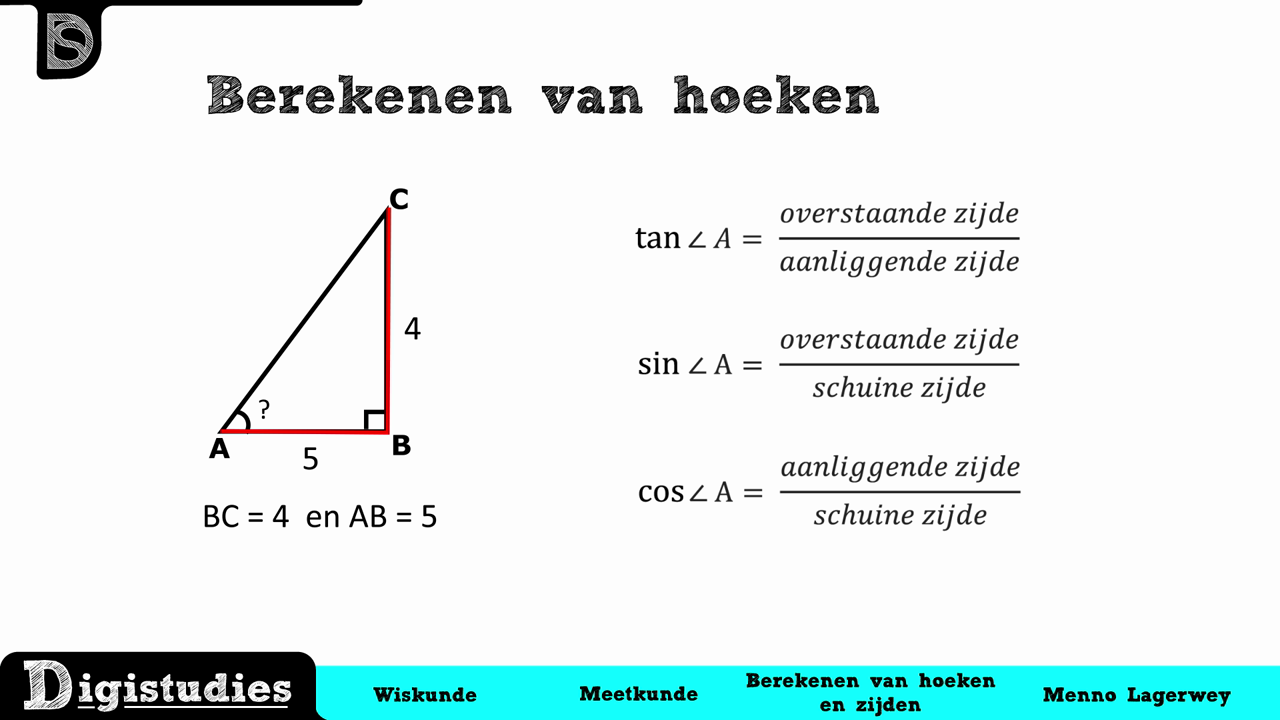
Digistudies Hoeken berekenen Wiskunde uitleg vmbo
Video met uitleg over het berekenen van hoeken met behulp van de tangens.Video's over sinus en cosinus:Sinus: https://youtu.be/jeTgyLt3PeACosinus: https://yo. In deze paragraaf leer je hoe je een hoek kunt berekenen met de tangens. Ook leer je dat je hoeken op twee verschillende manieren kunt noteren. Je moet hiervoor het ezelsbruggeltje TOA kennen. Ook moet je weten dat je een hoek berekent door de tan-1 (inverse tangens) te gebruiken. In het eerste filmpje hieronder vind je de uitleg.




