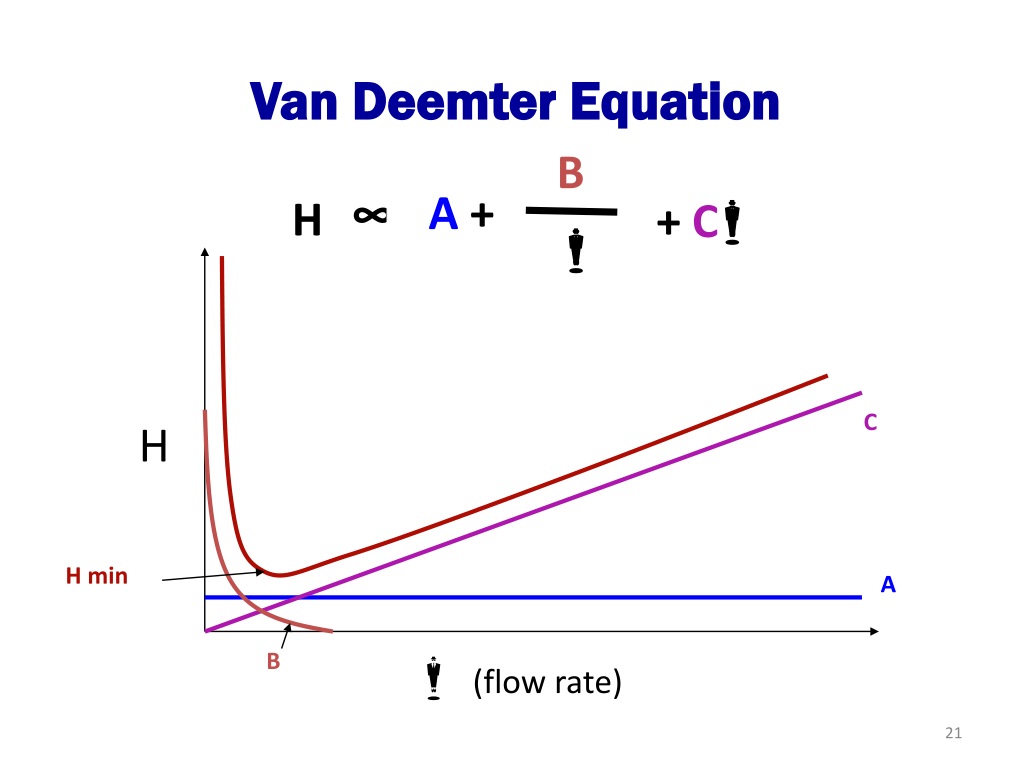
The van Deemter equation is a hyperbolic function that predicts that there is an optimum velocity at which there will be the minimum variance per unit column length and, thence, a maximum efficiency. The van Deemter equation was the result of the first application of rate theory to the chromatography elution process. Van Deemter equation The van Deemter equation is a theoretical treatment of the peak broadening within a chromatographic column. The equation, which describes the band broadening processes, is given by equation (3). (3) h = A + B v + C v where h - reduced plate height, a dimensionless measure of the band broadening. A, B, C are constants.

Van Deemter equation describes that efficiency varies with the linear... Download Scientific
By observing the Van Deemter equation, it can be deduced that an ideal mobile phase flow rate must be determined to yield the best (lowest) value of H. Decreasing the flow rate too much will result in an increase of the longitudinal diffusion factor B/u, while exceedingly increasing the flow rate will increase the significance of the mass transfer term Cu. Van Deemter equation - The Lockdown guide. Skip to Content. 01357 522 961. Quick Order. My Account. Register. Search. Search. Linear velocity is an important method parameter in chromatography and is affected by changes in flow rate, temperature, column dimensions, mobile phase type and is one of the more important factors t. In a simplified form, the Van Deemter equation is: HETP = A + (B / u) + Cu Where: A Eddy diffusion B Longitudinal diffusion C Resistance to mass transfer The effect of different carrier gases on column efficiency is represented by the van Deemter (packed columns) and the Golay equation (capillary columns). The van Deemter equation, \ref{2} , describes the three main effects that contribute to band broadening in packed columns and, as a consequence, to a reduced efficiency in the separation process.
PPT Van Deemter Equation PowerPoint Presentation, free download ID9536233
What we will develop as we analyze the four contributions to broadening above is an equation, which was first known as the van Deemter equation (J. J. van Deemter described the first treatment of this for chromatographic systems in 1956), that relates these four terms to the reduced plate height. Best known is the van Deemter equation, which describes the various contributions to plate height (H). In this equation the parameters that influence the overall peak width are expressed in three terms: H = HETP (plate height) A = eddy diffusion term B = longitudinal diffusion term u = linear velocity C = Resistance to mass transfer coefficient In 1956, van Deemter, Zuiderweg and Klinkenberg used the exact mathematical solution of Lapidus and Admundson and derived a considerably simplified equation that is the exact solution in the limit case when the column efficiency is significant and the eluted band profiles narrow. Access the complete (90 Videos) Analytical Chemistry Video Series here: https://chemguides.com/videos/Access FREE CONTENT here: https://chemguides.com/course.

Van Deemter equation is a hyperbolic function which indicates that... Download Scientific Diagram
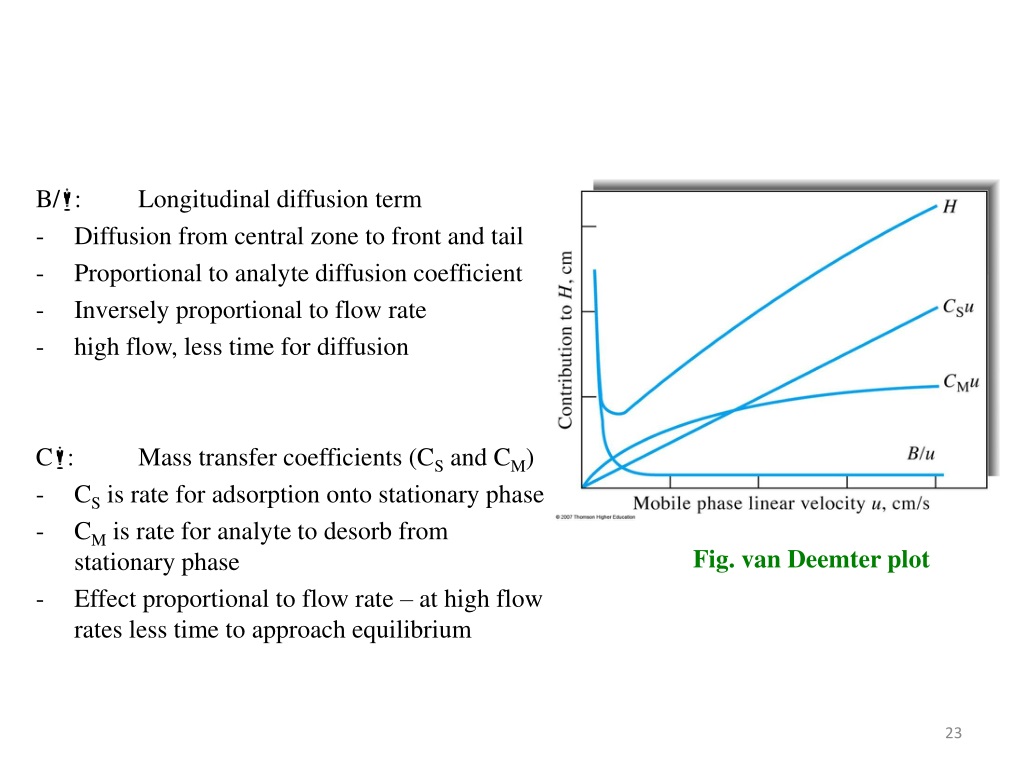
The fundamental mechanisms of band broadening are usually introduced to students through the van Deemter equation. Dimensional analysis of this equation can give physical meaning to the equation coefficients and enhance our understanding relative to qualitative descriptions. This approach can also guide improvements to future liquid chromatography (LC) column designs. The fundamental assumptions of the van Deemter height equivalent to a theoretical plate (HETP) equation were formulated nearly 60 years ago in its rigorous final mathematical derivation in 1956. The limit of applicability of this classical theory of band broadening in chromatographic columns is disc.
Van Deemter equation Mass transfer resistance in the mobile/stationary phase RPLC and HILIC columns reduced longitudinal diffusion coefficient sample concentration in the mobile phase (mol/m sample concentration in the stationary phase (mol/m reduced overall mass transfer resistance coefficient in the stationary phase As shown in Figure 12.3.7 —which uses the van Deemter equation—the optimum mobile phase velocity is the minimum in a plot of H as a function of u. Figure 12.3.7 . Plot showing the relationship between the height of a theoretical plate, H, and the mobile phase's velocity, u, based on the van Deemter equation.
PPT Van Deemter Equation PowerPoint Presentation, free download ID9536233
A gas chromatograph (GC) is an analytical instrument that measures the content of various volatile components in a sample. The analysis performed by a gas chromatograph is called gas chromatography. The Van Deemter equation is a hyperbolic function that predicts that there is an optimum velocity at which there will be the minimum variance per unit column length and, thence, a maximum efficiency. The Van Deemter equation was the result of the first application of rate theory to the chromatography elution process.




