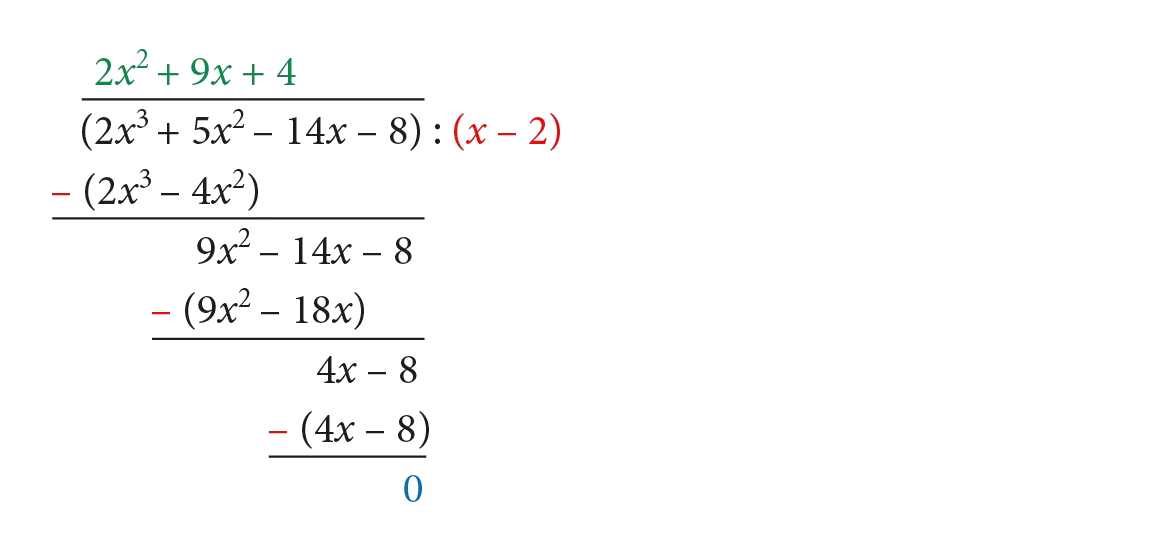dzielenie wielomianu przez trójmian. matematykaszkolna.pl. dzielenie wielomianu przez trójmian ksxr: Wykonaj dzielenie: (−2x 4 −10x 2 −18): (−x 2 +x−3) Krok po kroku jeśli można, nie wiem co zrobić gdy mam odejmować różne potęgi. 11 kwi 19:59. Kostek: https://matematykaszkolna.pl/strona/107.html. Przykład 1. Wykonaj dzielenie (x3 − 2x2 − 29x + 30): (x − 6) sposobem pisemnym. Przeanalizujmy sposób wykonania tego działania krok po kroku. 1. Aby móc wykonać dzielenie wielomianu sposobem pisemnym, musimy zacząć od następującego zapisu, który przypomina dzielenie pisemne liczb: ¯ (x3 − 2x2 − 29x + 30): (x − 6) 2.
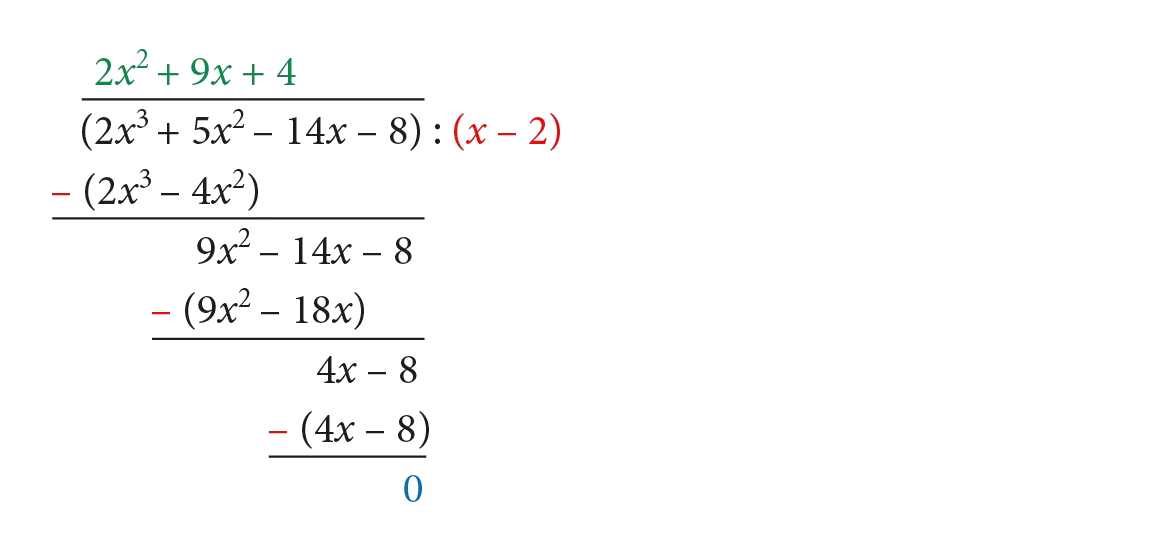
Dzielenie wielomianów dlaucznia.pl
Przykład 1 Wielomian jest podzielny przez wielomian , ponieważ istnieje wielomian taki, że jest spełniona równość: . Sprawdźmy: Tak samo jak przy dzieleniu pisemnym liczb, tak przy dzieleniu wielomianu przez inny wielomian możemy otrzymać resztę z dzielenia. Reszta z dzielenia wielomianu Twierdzenie: O dzieleniu wielomianów z resztą Dzielenie wielomianów podobne jest do dzielenia liczb całkowitych, gdzie podczas dzielenia otrzymujemy iloraz (wynik dzielenia) i resztę z dzielenia. Uwaga: Dzielenie wielomianów należy zacząć od uporządkowania wielomianów od największej do najmniejszej potęgi zmiennej x. Przykład dzielenia pisemnego wielomianów: (2x3 − 5x2 + 4x − 1): (x − 1) Podziękowania: 4 razy Otrzymane podziękowania: 9161 razy autor: Galen » 05 lis 2012, 22:27 Dzielisz pisemnie: (3x5 −x4 + x3 + 7x2 − 6x + 8): (x3 − x + 2) = 3x2 − x + 4 ( 3 x 5 − x 4 + x 3 + 7 x 2 − 6 x + 8): ( x 3 − x + 2) = 3 x 2 − x + 4 −3x5 + 3x3 − 6x2 − 3 x 5 + 3 x 3 − 6 x 2 ======================== Dzielenie wielomianów Metoda dzielenia wielomianów została dokładnie omówiona w poniższych nagraniach wideo. Zadanie 1. Wykonaj dzielenie poniższych wielomianów: a) b) c) Film Youtube Odp Zadanie 2. Wykonaj pisemne dzielenie liczb . Film Youtube Zadanie 3. Wykonaj dzielenie wielomianów . Film Youtube Zadanie 4. Wykonaj dzielenie wielomianów . Film

Dzielenie wielomianów Od Podstaw 8 MatFiz24.pl YouTube
Reszta z dzielenia wielomianu W(x) przez dwumian x+2 wynosi -4, a reszta z dzielenia tego wielomianu przez x-3 wynosi 5. Wyznacz resztę z dzielenia tego wielomianu przez x^2-x-6. Pierwiastek wielomianu. Dzielenie wielomianów. Układ równań 1. Definicja wielomianu 2. Obliczanie wartości wielomianu 3. Stopień wielomianu 4. Rozkład wielomianu na czynniki 5. Dodawanie i odejmowanie wielomianów 6. Dzielenie wielomianów 7. Równość wielomianów 8. Równania wielomianowe 9. Krotność pierwiastka wielomianu 10. Twierdzenie Bézouta 11. Wymierne pierwiastki wielomianu o współczynnikach całkowitych Dla n = 2 otrzymujemy funkcję kwadratową (trójmian kwadratowy) postaci f(x) = ax2 + bx+ c ; a , 0: Liczbę = b2 4ac nazywamy wyróznikiem trójmianu kwadratowego. (a)Jeśli < 0, to trójmian kwadratowy nie ma pierwiastków rzeczywistych. (b)Jeśli > 0, to trójmian kwadratowy ma dwa rnepierwiastki rzeczywiste określone wzorami x 1 = b p 2a. Okazuje się, że nie każde dzielenie wielomianów daje w rezultacie wielomian. Gdy nie daje, z dzielenia pozostaje nam reszta (tak, jak przy dzieleniu liczb całkowitych!). Gdy już umiemy dodawać, odejmować i mnożyć wielomiany, nadszedł czas, by nauczyć się je dzielić.

Dzielenie wielomianów przykłady mathflash YouTube
Reszta z dzielenia wielomianu W(x) = x3 − 2x2 + ax + 3 4 przez dwumian x − 2 jest równa 1. Oblicz wartość współczynnika a. W poniższe kratki wpisz kolejno trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku. Nie wykonując dzielenia, oblicz iloraz i resztę z dzielenia wielomianu f przez dwu-mian g, jeśli f(x) = x4 4x3 7x2 + 3x 20 , g(x) = x+ 2. Zadanie3. Resztazdzieleniawielomianu f przezdwumian(x+4)jestrówna4 ,aprzydzieleniu przez (x 2)jest równa 2. Oblicz resztę z dzielenia wielomianu f przez trójmian kwadratowy (x2 + 2x 8) . Zadanie 4.
W(x)=P(x)⋅G(x)+R(x). Wielomian R(x) nazywamy resztą z dzielenia wielomianu W(x) przez wielomian P(x), st R(x)
pomocy ! dzielenie wielomianów! Brainly.pl
Masz inny pomysł na rozwiązanie tego zadania? Napisz nam o tym! Rozwiązanie zadania z matematyki: Reszta z dzielenia wielomianu W (x) przez trójmian kwadratowy P (x)=x^2+2x-8 jest równaR (x)=-5x+2. Wyznacz resztę z dzielenia tego wielomianu przez dwumian (x+4).., Przez stopnia 1, 3846208. Przykład 1. Podzielmy wielomian przez wielomian . Pierwszy od lewej wyraz wielomianu dzielimy przez pierwszy wyraz dzielnika . Następnie mnożymy go przez dzielnik i mamy . Otrzymany wielomian podpisujemy pod dzielną i odejmujemy go od niej, np. poprzez dodanie wielomianu otrzymujemy pierwszą resztę z dzielenia: