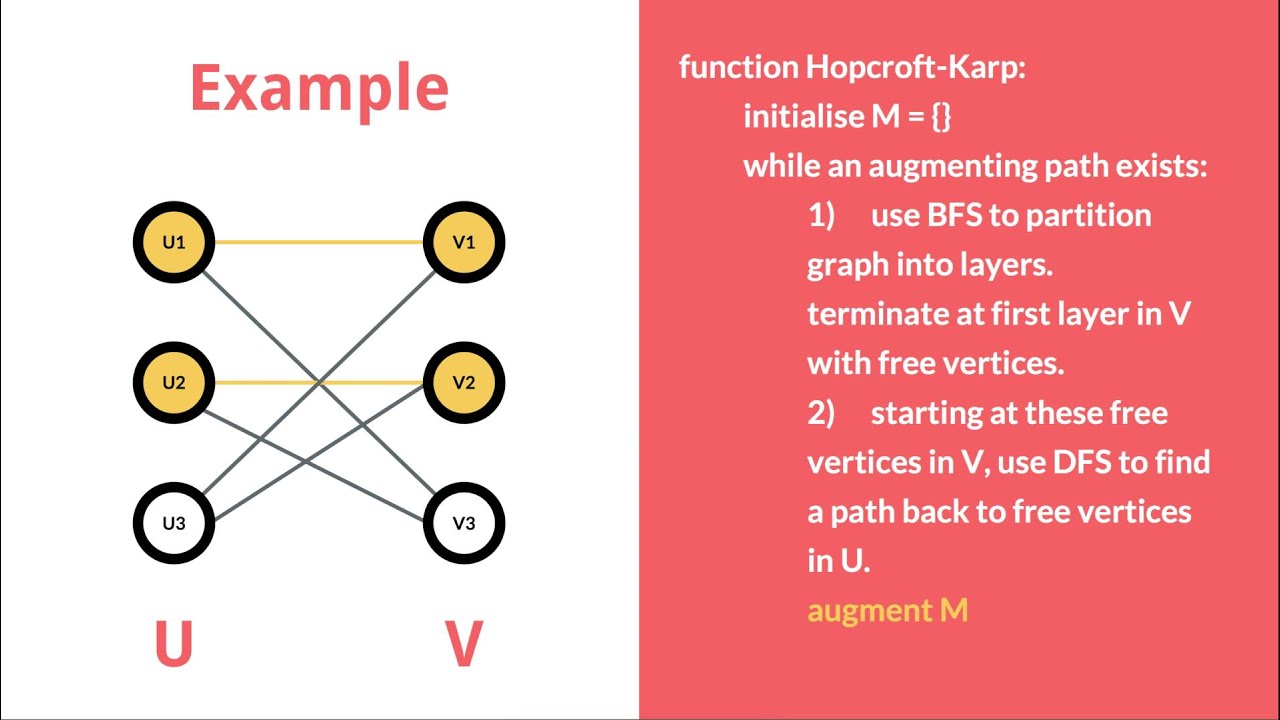
In computer science, the Hopcroft-Karp algorithm (sometimes more accurately called the Hopcroft-Karp-Karzanov algorithm) [1] is an algorithm that takes a bipartite graph as input and produces a maximum-cardinality matching as output — a set of as many edges as possible with the property that no two edges share an endpoint. Hopcroft Karp Algorithm: Initialize Maximal Matching M as empty. While there exists an Augmenting Path p Remove matching edges of p from M and add not-matching edges of p to M (This increases size of M by 1 as p starts and ends with a free vertex) Return M. Below diagram shows working of the algorithm.

HopcroftKarp Algorithm YouTube
Hopcroft-Karp Algorithm for Maximum Matching | Set 1 (Introduction) There are few important things to note before we start implementation. We need to find an augmenting path (A path that alternates between matching and not matching edges, and has free vertices as starting and ending points). The Hopcroft-Karp algorithm is an algorithm that takes a bipartite graph G (E,V) G(E,V) and outputs a maximum matching, M M. It runs in worst-case O\big (|E| \sqrt {|V|}\big) O(∣E ∣ ∣V ∣) time. The Hopcroft-Karp algorithm uses similar techniques as the Hungarian algorithm and Edmonds' blossom algorithm. The Hopcroft-Karp algorithm is an algorithm that takes as input a bipartite graph and produces as output a maximum cardinality matching, it runs in O (E √V) time in worst case. Let us define few terms before we discuss the algorithm. Bipartite graph In this section we introduce the bipartite maximum matching problem, present a na ve algorithm with O(mn) running time, and then present and analyze an algorithm due to Hopcroft and Karp that improves the running time to O(m p n). 1.1 De nitions De nition 1.
hopcroftkarp algorithm YouTube
An explanation of the Hopcroft-Karp algorithm. Created by Joromy Bou Khalil and Wesley Williams, University of Bristol. Here we demonstrate the Hopcroft-Karp algorithm that solves the problem of finding maximal matchings on bipartite graphs. What do you want to do first? Test the algorithm! Read detailed description of the algorithm This applet demonstrates the Hopcroft-Karp Algorithm How does the Hopcroft-Karp algorithm work? Ask Question Asked 12 years, 6 months ago Modified 8 years, 8 months ago Viewed 8k times 11 I am currently working on a project to pictorially explain the Hopcroft-Karp algorithm. I am using the pseudo-code from the Wikipedia article. I have also seen this algorithm implemented on Stack Overflow in Python 1 Hopcroft-Karp Algorithm Recall that the basic bipartite matching algorithm repeatedly nds an augmenting path and performs the operation M L E(P), where P is the augmenting path found at each iteration, until the graph has no more augmenting paths. The running time of the algorithm is O(mn), as an augmenting paths can

HopcroftKarp Algorithm YouTube
The Augmenting path algorithm seen in class chooses one augmenting path in each iteration, even if it nds many augmenting paths in the process of searching. The Hopcroft-Karp algorithm improves the running time of the above algorithm by correcting this wasteful aspect; in each iteration it attempts to nd many disjoint augmenting paths, and it. This is a video explaining the operations of the Hopcroft-Karp algorithm, which is an algorithm which takes as input a bipartite graph and provides as output.
1 Dinitz's Algorithm Dinitz's Algorithm improves the Edmonds-Karp Algorithm by discovering a blocking ow, which is in some sense a maximal set of shortest augmenting paths that can be used simul-taneously to update the current ow without violating capacity constraints. De nition 1. Welcome to our in-depth tutorial on understanding maximum matchings in bipartite graphs using the Hopcroft-Karp algorithm. In this video, we dive into the in.

The HopcroftKarp Algorithm YouTube
-1 I am working on graph algorithm theories (I am mathematician nothing with computer science yet) and I do have some matching problems to self, for which I am using Hopcroft-Karp for serious reasons ( Hopcroft-Karp algorithm ). I don't want to solve them by hand with it, so I would like to use a program for it. The time complexity of the Hopcroft-Karp Algorithm for maximum matching is O(√V x E), where E is the number of Edges and V is the number of vertices. Space Complexity. The space complexity of the Hopcroft-Karp Algorithm is O(V) as we are using extra space for storing u and v. Check out this problem - Check If A String Is Palindrome




