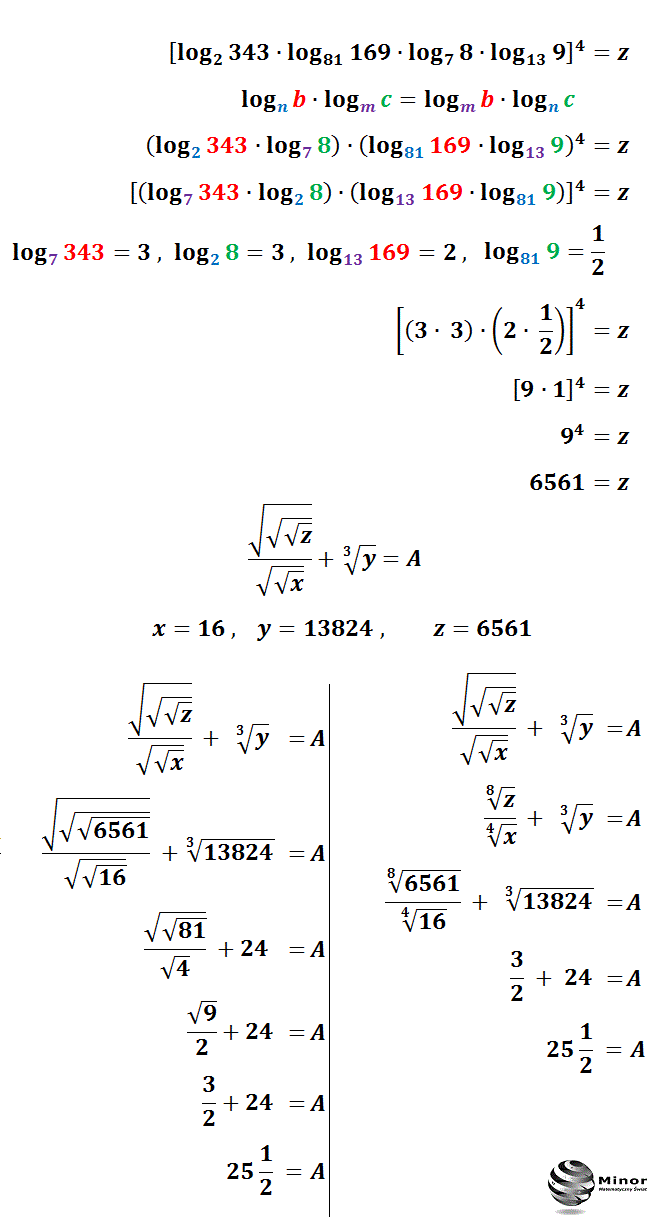Jeśli chcemy dodać do siebie logarytmy o tych samych podstawach korzystamy ze wzoru. logax +logay =loga(x ⋅y) l o g a x + l o g a y = l o g a ( x ⋅ y) Przykłady: Przedstaw logarytm w prostszej postaci. log24+log25 l o g 2 4 + l o g 2 5 = log2(4 ⋅5) = log220 = l o g 2 ( 4 ⋅ 5) = l o g 2 20. Dwa logarytmy o takiej samej podstawie dodajemy korzystając ze wzoru: loga b +loga c =loga(b ⋅ c) Z bardzo podobnego wzoru korzystamy, gdy chcemy odjąć logarytmy o wspólnej podstawie: loga b −loga c = loga(b c) Przykład 1. Oblicz log2 2 +log2 8. Rozwiązanie: log2 2 +log2 8 = log2(2 ⋅ 8) =log2 16 = 4 Przykład 2. Oblicz log2 2 −log2 8. Rozwiązanie:

Zadanie dodawanie logarytmów YouTube
Definicja Logarytmem liczby b przy podstawie a nazywamy taką liczbę c, że a podniesione do potęgi c daje liczbę b. Matematycznie zapiszemy tę definicję tak: loga b = c to ac = b Zatem żeby obliczyć loga b, wystarczy odpowiedzieć na pytanie: Do jakiej potęgi podnieść liczbę a, żeby otrzymać liczbę b? podstawa logarytmu . Liczba "c" to jest liczba logarytmowana , natomiast liczba "b" to jest właśnie logarytm . Tyle jeśli chodzi o nazwy. Liczby te muszą, zgodnie z tym co jest napisane w tablicach, spełniać określone warunki tzn. Rozwiązanie zadania. Dodawanie logarytmów o równych podstawach: log_15 3 + log_15 5, log 4 + log 25, log_4 8 + log_4 32 Oba logarytmy mają tą samą podstawę, więc możemy skorzystać ze wzoru na dodawanie logarytmów i zapisać, że: log24 + log22 = log2(4 ⋅ 2) = log28 = 3 l o g 2 4 + l o g 2 2 = l o g 2 ( 4 ⋅ 2) = l o g 2 8 = 3

Własności i działania na logarytmach Aa School, Middle School Math
Sprawdź z jakich wzorów i własności można skorzystać na mnożenie, dzielenie, dodawanie, odejmowanie logarytmów o tych samych i różnych podstawach. Dowód działania 7, 8, 9, 10 Wiesz jak obliczyć x, y, z korzystając w podanych własności i działań na logarytmach? Sprawdź Post nr 491 Autor: Robert Karolewski o 15:49 1. Skorzystaj ze wzoru na sumę logarytmów o tej samej podstawie. Jeśli dodajemy do siebie dwa logarytmy o tej samej podstawie to w rezultacie dostajemy jeden logarytm przy tej samej podstawie z liczby, która jest iloczynem (mnożeniem) liczb logarytmowanych. 2. Skorzystaj z definicji logarytmu. Zamieniając równanie z postaci logarytmicznej w postać wykładniczą lub z postaci wykładniczej w postać logarytmiczną, należy pamiętać, że podstawa logarytmu jest taka sama jak podstawa wykładnika. Youtube Metoda liczenia logarytmów Przypuśćmy, że musimy obliczyć loga b. Wynik takiego działania oznaczamy sobie przez x. Zatem mamy: loga b = x Zgodnie z definicją logarytmu możemy teraz przekształcić to równanie na następujące: ax = b Teraz z otrzymanego równania wyliczamy liczbę x.
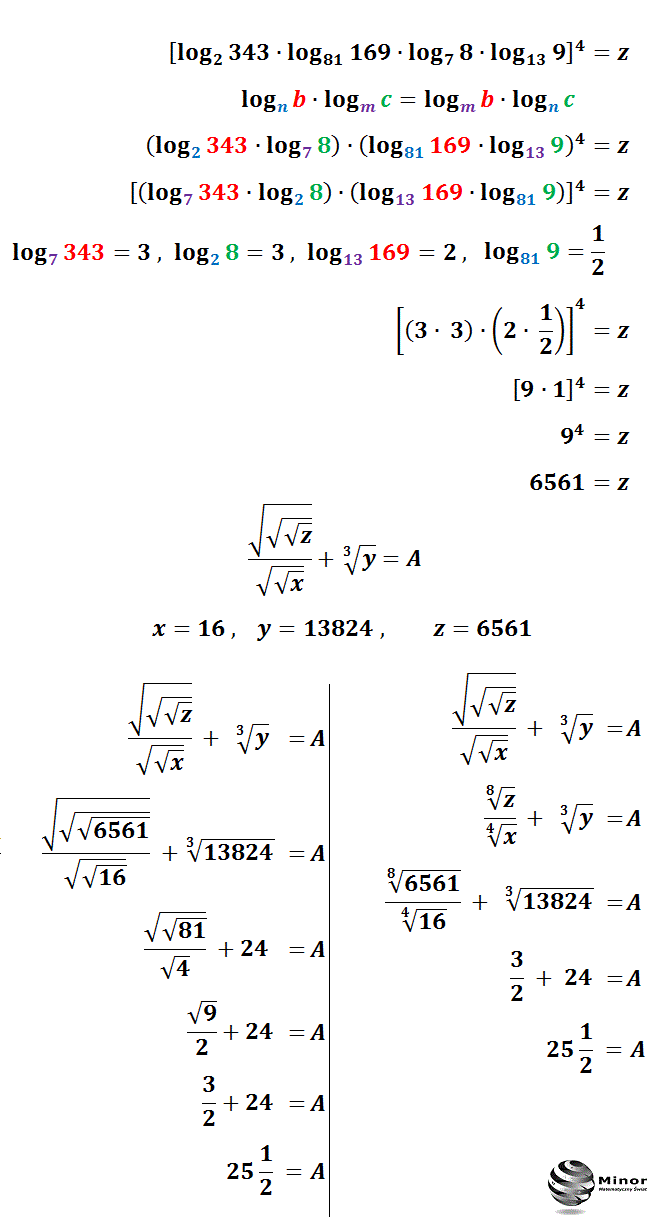
Blog matematyczny Minor Matematyka Mnożenie logarytmów
Logarytmy jak każdą inną liczbę możemy dodawać, odejmować, mnożyć i dzielić. Gdy podstawa logarytmu jest taka sama to mamy na to konkretne wzory z których bardzo często bedziesz korzystał. Gdy podstawa jest inna to jest to troche bardziej skomplikowane i często trzeba trochę pogłówkować, aby znaleźć dobry sposób na. Zapisz się dzisiaj. Własności logarytmów. Logarytmy - najważniejsze wzory. Dodawanie i odejmowanie logarytmów. Zmiana podstawy logarytmu. Równania logarytmiczne. Funkcja logarytmiczna. Logarytm naturalny. Logarytm dziesiętny.
Logarytmy wzory - podsumowanie. Poniżej prezentuję najważniejsze wzory logarytmiczne w postaci krótkiego podsumowania. Wszystkie te wzory znajdziesz również w tablicach matematycznych w czasie matury. Przykłady obrazujące powyższe wzory na logarytmy znajdziesz w tematach w dziale logarytmy. Znajdziesz tam też zadania maturalne i nie. Przykład 1. Oblicz log2 6 +log2 2 3. Rozwiązanie: Korzystamy ze wzoru na dodawanie logarytmów: loga b +loga c = loga(b ⋅ c): log2 6 +log2 2 3 =log2(6 ⋅ 2 3) =log2 4 = 2 Przykład 2. Oblicz log3 18 −log3 2. Rozwiązanie: Korzystamy ze wzoru na odejmowanie logarytmów: loga b −loga c = loga(b c): log3 18 −log3 2 = log3(18 2) = log3 9 = 2 Przykład 3.

Logarytm Z 0 Ucz się matematyki za darmo
Logarytmy - wzory. Aby szybko dokonywać obliczeń, warto poznać najważniejsze wzory. Dotyczą one: dodawania logarytmów o tej samej podstawie, odejmowania logarytmów o tej samej podstawie, wyciągania wykładnika przed logarytm. Jeżeli: to mamy do czynienia z następującymi wzorami: - dodawanie logarytmów o tej samej podstawie Logarytm jest funkcją odwrotną do funkcji wykładniczej. Dzięki logarytmom możemy łatwo rozwiązywać równania, w których występują funkcje wykładnicze. Poza tym jest to dobra okazja, by wejść głębiej w relację pomiędzy funkcją a funkcją do niej odwrotną..