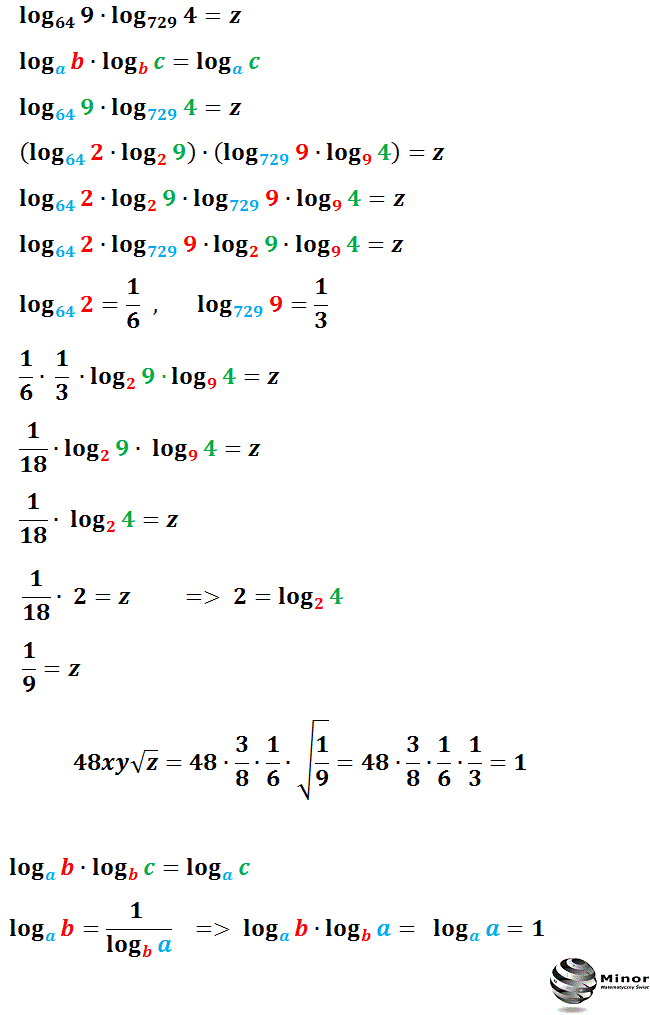Mnożenie logarytmów o tych samych podstawach Na mnożenie logarytmów nie ma żadnych wzorów. Postępujemy tak jak w przypadku dodawania\odejmowania logarytmów o różnych podstawach, tzn "na marginesie" obliczamy każdy z logarytmów, a następnie gotowe wyniki wymnażamy. Przykład 2:log216⋅ log327 =. l o g 2 16 ⋅ l o g 3 27 =.. = 4 ⋅3 =12. = 4 ⋅ 3 = 12 Wzór logarytmu wygląda tak: logab = c Wtedy i tylko wtedy, gdy: ac = b Poszczególne litery tego ogólnego wzoru odczytamy następująco: a - podstawa logarytmu b - liczba logarytmowana c - logarytm Logarytm przy podstawie a z liczby b wynosi c.
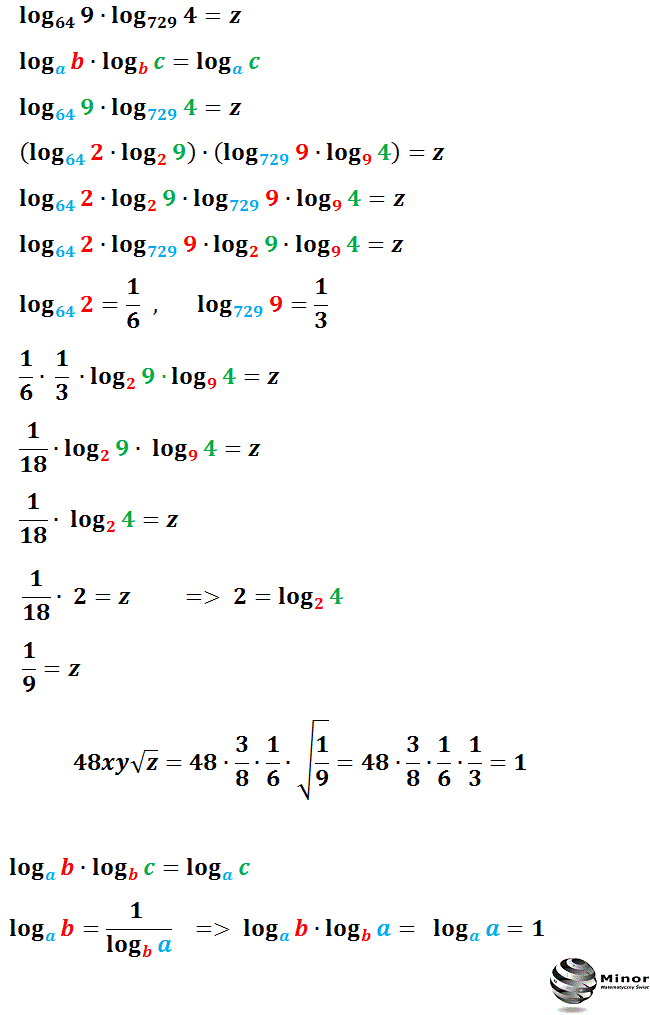
Blog matematyczny Minor Matematyka Mnożenie logarytmów
Mnożenie logarytmów o różnych podstawach Wyznacz wartość wyrażeń x, y, z zapisanych za pomocą logarytmów a następnie oblicz wartość wyrażenia 48xy√z. Rozwiązanie I: Pomiędzy logarytmami o różnych podstawach zachodzi związek: Obliczamy wartość wyrażenia x: Obliczamy wartość wyrażenia y: Obliczamy wartość wyrażenia z: Rozwiązanie II: Sprawdź z jakich wzorów i własności można skorzystać na mnożenie, dzielenie, dodawanie, odejmowanie logarytmów o tych samych i różnych podstawach. Dowód działania 7, 8, 9, 10 Wiesz jak obliczyć x, y, z korzystając w podanych własności i działań na logarytmach? Sprawdź Post nr 491 Autor: Robert Karolewski o 15:49 Rozwiązanie: Korzystamy ze wzoru na odejmowanie logarytmów: loga b −loga c = loga(b c): log3 18 −log3 2 = log3(18 2) = log3 9 = 2 Przykład 3. Wyciąganie wykładnika potęgi przed logarytm: log273 = 3log2 7 = log21 3 7 = log 2√3 7 W tym przykładzie wykorzystaliśmy wzory: loga(bn) = n ⋅loga b logan b = 1 nloga b Przykład 4. Logarytmy - najważniejsze wiadomości W tym nagraniu wideo omawiam najważniejsze wiadomości dotyczące logarytmów. Pokazuję najprostszą metodę obliczania logarytmów, omawiam wszystkie najważniejsze wzory związane z logarytmami, dziedzinę logarytmu oraz równania i nierówności logarytmiczne. Czas nagrania: 67 min. Film Youtube Definicja

Mnożenie i dzielenie potęgo tej samej podstawie Brainly.pl
Wzory. Dwa logarytmy o takiej samej podstawie dodajemy korzystając ze wzoru: loga b +loga c =loga(b ⋅ c) Z bardzo podobnego wzoru korzystamy, gdy chcemy odjąć logarytmy o wspólnej podstawie: loga b −loga c = loga(b c) Przyglądamy się bliżej dowodom własności logarytmów: wzorom na logarytm iloczynu, logarytm ilorazu oraz logarytm liczby podniesionej do potęgi. W tej lekcji dowiedziemy trzy własności logarytmów: na sumę i różnicę logarytmów o tych samych podstawach i na mnożenie logarytmu przez liczbę. Wzór na zmianę podstawy logarytmu. Stosując następującą metodę możemy zamienić podstawę dowolnego logarytmu: log b ( a) = log x ( a) log x ( b) Uwagi: Nowa podstawa, x. . , może mieć dowolną wartość. Jak zawsze, aby ten wzór był prawdziwy, argumenty logarytmów muszą być dodatnie a ich podstawy dodatnie i różne od 1. . Proszę zauważyć, że log25 z 1 = 0, a zatem całe mnożenie wyjdzie 0. Nie ma sensu liczyć 1/2*log25 z 5 (BTW.. Mamy tu iloczyn potęg o tej samej podstawie, wiec: A=10^6,2+(−4) czyli 10^2,2. Odpowiedz. Ania W końcu ogarnęłam logarytmy : D dzięki!. To w sumie wynika wprost z istoty logarytmów, bo jak masz przykładowo log5 z 5.

Mnożenie logarytmów Kreatywna matematyka dla dzieci
Aby obliczyć logarytm o podstawie a z liczby x zadajemy sobie pytanie: "do jakiej potęgi musimy podnieść podstawę aby otrzymać x". ⓘ Przykład: Logarytm dziesiętny (o podstawie 10) z liczby sto (100), to dwa (2), ponieważ aby otrzymać tę liczbę (100), musielibyśmy podnieść podstawę logarytmu (10) do drugiej potęgi. Można to wyrazić za pomocą równania logarytmicznego log 2 ( 16) = 4 , które czytamy jako "logarytm o podstawie dwa z szesnastu równa się cztery". Oba równania wyrażają tę samą zależność pomiędzy liczbami 2 , 4 , oraz 16 , gdzie 2 to podstawa, a 4 to wykładnik. Różnica między potęgą a logarytmem polega na tym, że wynikiem.
Wyzwanie Sprawdź swoje umiejętności w zakresie objętym tą ścieżką. Zacznij wyzwanie z kursu Matematyka Algebra 2 Część 8: Logarytmy Do zdobycia jest 900 punktów za mistrzostwo Opanowane Biegły Zaznajomiony Podjęto próbę Nierozpoczęte Quiz Test sprawdzający O tym dziale Logarytm jest funkcją odwrotną do funkcji wykładniczej. autor: abc666 » 28 lis 2009, o 21:14 Nie.=6log26. = 6 log 2 6 Dasio11 Moderator Posty: 10127 Rejestracja: 21 kwie 2009, o 18:04 Płeć: Mężczyzna Lokalizacja: Wrocław Podziękował: 39 razy Pomógł: 2337 razy Mnozenie logarytmow o takiej samej podstawie problem/

19. Dodawanie logarytmów o tej samej podstawie YouTube
W tym wyrażeniu , oraz są liczbami. Zazwyczaj znamy liczby i , a musimy znaleźć liczbę (czyli obliczyć logarytm). W gruncie rzeczy logarytm to po prostu odwrotność potęgowania. Spójrz na przykłady: , ponieważ ; , ponieważ ; , ponieważ . Być może zastanawiasz się, po co w takim razie komplikować sobie życie logarytmami, skoro mamy potęgi. Wzory wykorzystywane do liczenia logarytmów wraz z przykładami ich użycia. matematykaszkolna.pl.. komentarze do tej strony (55) forum zadankowe. Wzory. Logarytmy. Logarytm z 1. Logarytm o takiej samej podstawie jak liczba logarytmowana. Dodawanie i odejmowanie logarytmów. Zamiana podstawy w logarytmie.