1 2 ⋅ 2 3 ⋅ 3 4. Rozwiązanie: a) 2 5 ⋅ 3 7 = 2 ⋅ 3 5 ⋅ 7 = 6 35. b) 3 4 ⋅ 2 5 = 3 ⋅ 2 4 ⋅ 5 = 6 20 = 3 10. Na końcu wykonaliśmy skrócenie ułamka (podzieliliśmy licznik i mianownik przez 2 ). Ułamek można skrócić również wcześniej - przed wykonaniem mnożenia: 3 ⋅ 2 4 ⋅ 5 = 3 ⋅ 1 2 ⋅ 5 = 3 10. Mnożenie ułamków zwykłych o takich samych i różnych mianownikach
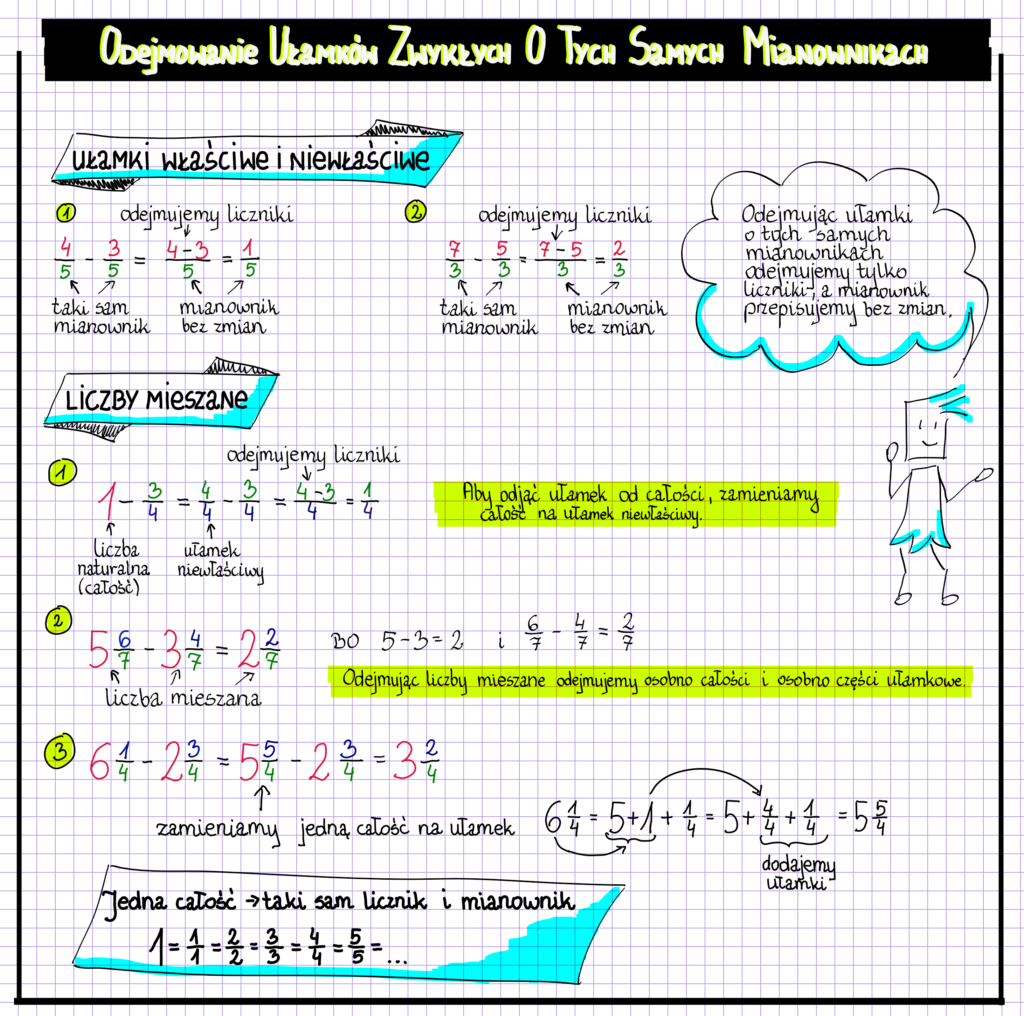
DODAWANIE I ODEJMOWANIE UŁAMKÓW O TYCH SAMYCH MIANOWNIKACH
Aby dodać i odjąć ułamki, pierwszą rzeczą, którą musimy zrobić, to sprawdzić, czy mianowniki są takie same, czy nie, ponieważ będzie to zależeć od tego, jak zostanie przeprowadzona operacja. Dodawanie i odejmowanie ułamków zwykłych o tym samym mianownik - Kalkulator do ułamków Mnożenie ułamka przez ułamek. Aby pomnożyć ułamek przez ułamek, należy pomnożyć licznik pierwszego ułamka przez licznik drugiego, a mianownik pierwszego ułamka pomnożyć przez mianownik drugiego ułamka. Przykład 1. Ułamki, których mianowniki nie są takie same to ułamki niepodobne. Na przykład: $$\frac{1}{2}, \frac{3}{7}, \frac{7}{11}$$ Ułamki Równe. Jeśli można uprościć ułamki do takiej samej formy, nazywamy je ułamkami równymi. Na przykład: $$\frac{1}{3}, \frac{2}{6}, \frac{4}{12}$$ Wszystkie te ułamki można uprościć do \$\frac{1}{3}\$. Dodawanie ułamków o tym samym mianowniku. Dodawanie ułamków o tym samym mianowniku - Ćwiczenie pomoże Ci utrwalić dodawanie ułamków zwykłych, które mają ten sam mianownik. Wybierz jedną z trzech odpowiedzi, która jest poprawnym wynikiem przedstawionego działania.

Kalkulator ułamków mnożenie, dodawanie, dzielić Kalkulatory Online
Rozwiń ułamki do ich odpowiedników o wspólnym mianowniku: 4 / 10 i 3 / 10. Odejmij liczniki. 2 / 5 - 3 / 10 = 4 / 10 - 3 / 10 = 1 / 10. Dla ułamków mieszanych (2 3 / 5 i 1 1 / 2): Zamień ułamki mieszane na ułamki niewłaściwe tak jak poprzednio: 2 3 / 5 = 13 / 5 i 1 1 / 2 = 3 / 2. Odejmij dwa ułamki niewłaściwe o różnych. Aby odjąć dwa ułamki o różnych mianownikach, trzeba je najpierw sprowadzić do tego samego mianownika i postępować tak, jak w przykładzie 2. 3 10 - 1 15 = 9 30 - 2 30 = 9 - 2 30 = 7 30 Staramy się, żeby wspólny mianownik ułamków był najmniejszą wspólną wielokrotnością mianowników. Twoim zadaniem jest wybranie jednej z trzech prawidłowych odpowiedzi, pamiętając o skracaniu ułamków, które będą wynikiem naszych obliczeń. To pomoże Ci rozwiązać powyższe zadanie: Dodawanie i odejmowanie ułamków zwykłych Skracanie ułamków. Wartością wyrażenia jest liczba uzyskana z dzielenia liczby przez liczbę . Wartość nazywamy licznikiem , a wartość nazywamy mianownikiem. Mianownik musi być liczbą różną od zera, gdyż, jak wiemy, dzielenie przez zero nie ma wartości.

Mnożenie ułamków zwykłych o takich samych i różnych mianownikach YouTube
W tym przypadku można jednak uzyskać mniejszy wspólny mianownik, stosując następujące rozszerzenia: 1 6 = 1 ⋅ 2 6 ⋅ 2 = 2 12 oraz 3 4 = 3 ⋅ 3 4 ⋅ 3 = 9 12 Tym razem oba ułamki doprowadziliśmy do mianownika równego 12. Generalnie opłaca się doprowadzać ułamki do jak najmniejszego mianownika, ponieważ na małych liczbach łatwiej wykonuje się rachunki. Aby obliczyć wynik mnożenia ułamków w tym kalkulatorze, wprowadź oba ułamki i naciśnij przycisk =. Kalkulator oprócz samego wyniku powinien wygenerować także szczegółowe obliczenia wraz z opcjonalnym, uproszczonym wynikiem. Aby obliczyć wynik mnożenia ułamków: Pomnóż wszystkie liczniki. Pomnóż wszystkie mianowniki.
Odejmujemy od siebie liczniki ułamków, mianownik przepisujemy bez zmian. Otrzymany wynik można uprościć poprzez skrócenie otrzymanego ułamka, ponieważ liczby 6 i 9 mają wspólny dzielnik przez który możemy je podzielić. Temat jakim będziemy się zajmować dotyczy dodawania i odejmowania ułamków o tym samym mianowniku. Poznacie sposoby na dokonywanie obliczeń przy ułamkach zwykłych, rozwiążemy wspólnie kilka przykładów i zadań.

Kodowana karta pracy dodawanie i odejmowanie ułamków dla klasy 4
A więc zróbmy to. 5/6 * 2/3 Mnożenie ułamków jest bardzo łatwe. Nowy licznik, to znaczy licznik wyniku mnożenia to po prostu pomnożone oba liczniki. Górna liczba to wynik mnożenia obu liczb na górze. Więc licznik wyniku jest równy 5 * 2. 5 * 2 w liczniku… i 6 * 3 w mianowniku. 5 * 2 = 10 6 * 3 = 18.wynik to 10/18. osi liczbowej, porównywanie ułamków, dodawanie i odejmowanie ułamków zwykłych o jednakowych mianownikach. W klasie V: utrwalenie umiejętności z klasy IV; działania na ułamkach zwykłych o różnych mianownikach; obliczanie ułamka danej liczby; obliczanie liczby z danego jej ułamka.




