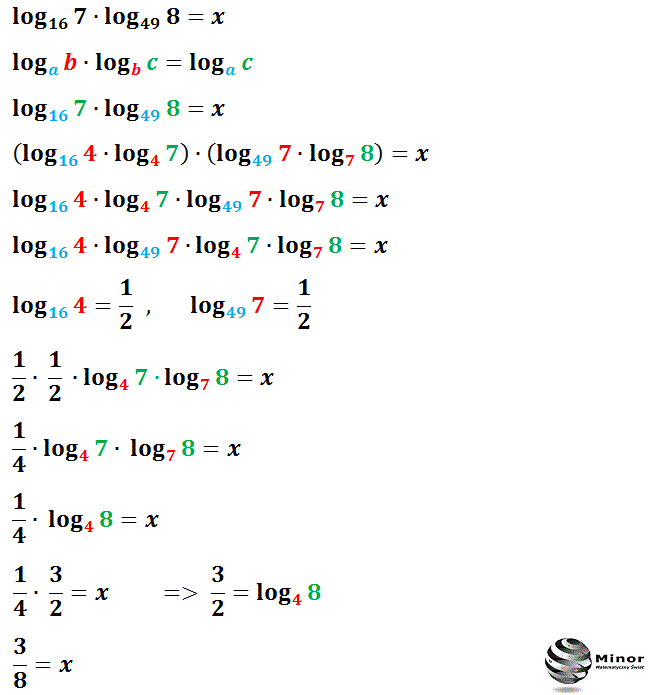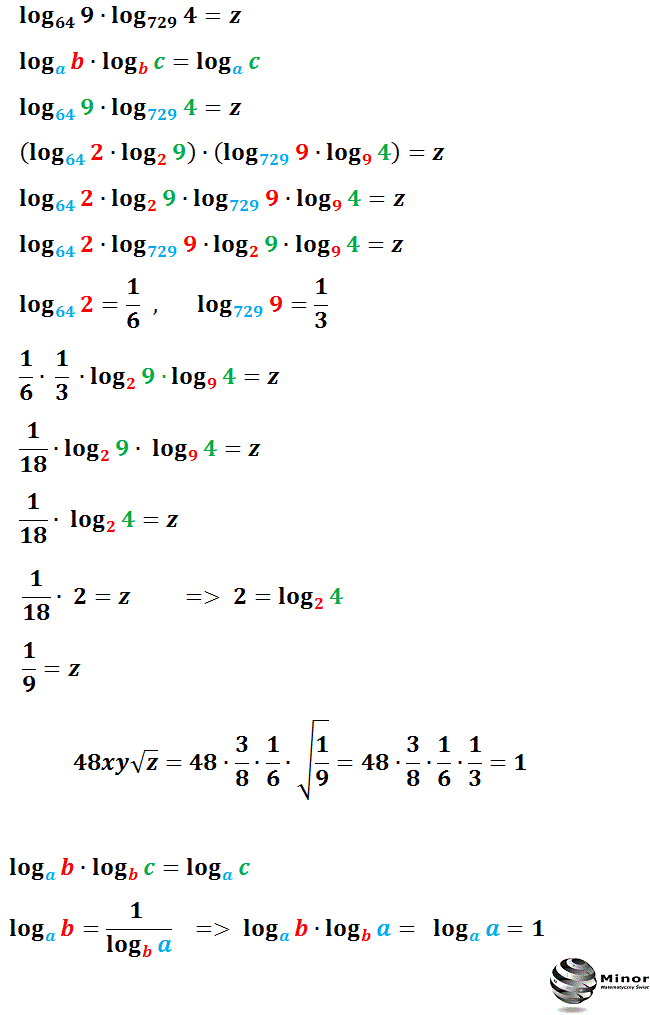Mnożenie logarytmów o różnych podstawach Wyznacz wartość wyrażeń x, y, z zapisanych za pomocą logarytmów a następnie oblicz wartość wyrażenia 48xy√z. Rozwiązanie I: Pomiędzy logarytmami o różnych podstawach zachodzi związek: Obliczamy wartość wyrażenia x: Obliczamy wartość wyrażenia y: Obliczamy wartość wyrażenia z: Rozwiązanie II: Działania na logarytmach Działania na logarytmach - dodawanie logarytmów o tych samych podstawach Jeśli chcemy dodać do siebie logarytmy o tych samych podstawach korzystamy ze wzoru logax +logay =loga(x ⋅y) l o g a x + l o g a y = l o g a ( x ⋅ y) Przykłady: Przedstaw logarytm w prostszej postaci.
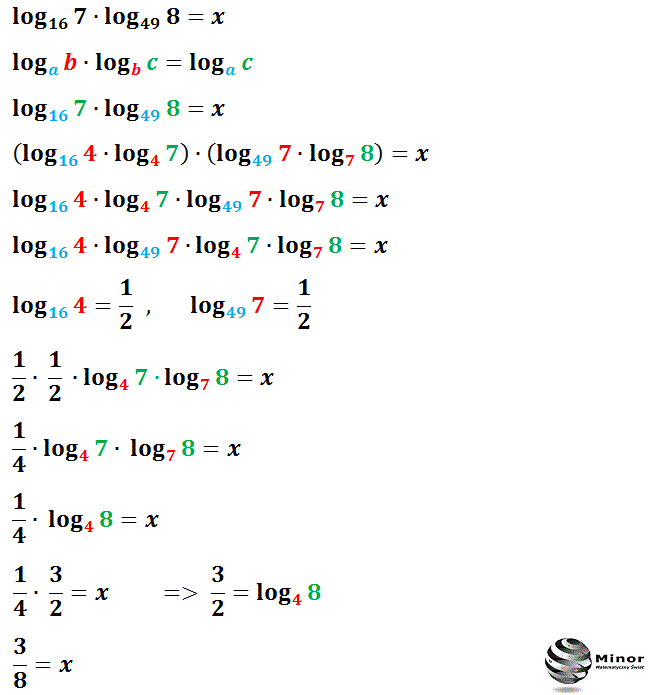
Blog matematyczny Minor Matematyka Mnożenie logarytmów
a - podstawa logarytmu b - liczba logarytmowana c - logarytm Logarytm przy podstawie a z liczby b wynosi c. Należy pamiętać również o tym, że podstawa logarytmu, czyli w naszym przykładzie a, musi być większa od 0 i różna od 1. Z kolei liczba logarytmowana, czyli nasze b wynosić musi więcej niż 0. Mnożenie logarytmów o tej samej podstawie Sprawdź z jakich wzorów i własności można skorzystać na mnożenie, dzielenie, dodawanie, odejmowanie logarytmów o tych samych i różnych podstawach. Dowód działania 7, 8, 9, 10 Wiesz jak obliczyć x, y, z korzystając w podanych własności i działań na logarytmach? Sprawdź Post nr 491 Autor: Robert Karolewski o 15:49 Definicja Logarytmem liczby b przy podstawie a nazywamy taką liczbę c, że a podniesione do potęgi c daje liczbę b. Matematycznie zapiszemy tę definicję tak: loga b = c to ac = b Zatem żeby obliczyć loga b, wystarczy odpowiedzieć na pytanie: Do jakiej potęgi podnieść liczbę a, żeby otrzymać liczbę b? Rozwiązanie: Załóżmy, że loga b = c. Wówczas mamy: ac = b Możemy podnieść obie strony równania do potęgi n: anc = bn Teraz zapisujemy równanie w postaci logarytmicznej korzystając z definicji logarytmu: logabn = nc Skoro loga b = c, zatem mamy: logabn = n ⋅loga b Przykład 5. Wykaż, że zachodzi wzór: logan b = 1 nloga b Rozwiązanie:

Mnożenie logarytmów Kreatywna matematyka dla dzieci
W tej lekcji dowiedziemy trzy własności logarytmów: na sumę i różnicę logarytmów o tych samych podstawach i na mnożenie logarytmu przez liczbę. Zanim jednak zaczniemy, przypomnijmy sobie przydatną własność, która pomoże nam w dalszej pracy. log b ( b c) = c Innymi słowy, logarytm o podstawie b odwraca efekt podnoszenia liczby b do potęgi! Rozwiązanie: log2 2 −log2 8 =log2(2 8) = log2(1 4) = −2 Zadanie 1. Oblicz log6 3 +log6 12. Film Youtube Odp Zadanie 2. Oblicz log8 32 +log8 2. Film Youtube Odp Zadanie 3. Oblicz log2 4 +log2 8. Film Youtube Odp Zadanie 4. Oblicz log 25 + log 40. Film Youtube Odp Zadanie 5. Oblicz log5 50 −log5 2. Film Youtube Liczba ta jest iloczynem dwóch pierwszych liczb, tzn: 8192 x 131072 = 1073741824. Ze wzorów na dodawanie i odejmowanie logarytmów wynikają ich własności: Wyprowadźmy jeszcze jeden ważny wzór, który pozwoli nam przeliczać logarytmy z jednej podstawy na inną. Problem jest następujący: Znamy wartość logarytmu przy podstawie a z. Udowadniamy wzory na logarytm różnicy, log (a) - log (b) = log (a/b), oraz na mnożenie logarytmu przez liczbę, k⋅log (a) = log (aᵏ). Stworzone przez: Sal Khan. asmolinski303 7 miesięcy temu A nie na róznicę logarytmów? Odpowiedź • ( 1 głos) Zaglosuj za Zagłosuj przeciw Flaga Następny materiał: artykuł
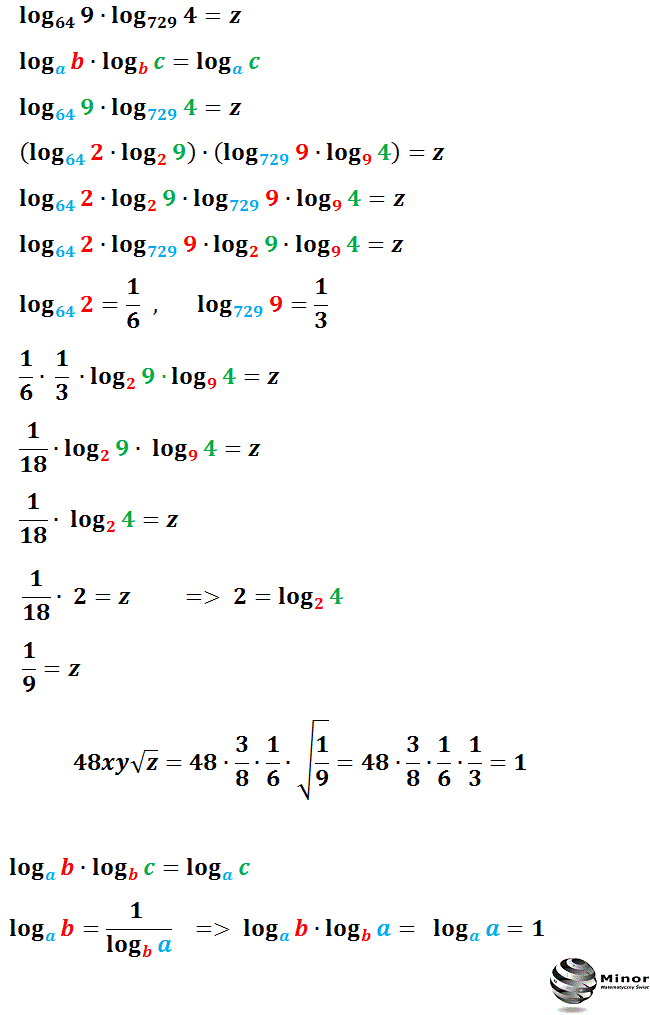
Blog matematyczny Minor Matematyka Mnożenie logarytmów
Bez poniższych własności logarytmów, logarytmowanie byłoby bardzo trudne. Przedstawione wzory wykorzystujemy często w analizie matematycznej. Z definicji logarytmu, a także z własności działań na potęgach dla a ∈ R + ∖ { 1 } oraz b, c ∈ R + prawdziwe są wszystkie poniższe zależności: Dowolny logarytm z 1 jest równy zeru. W takim wypadku musimy najpierw obliczyć każdy z logarytmów, a następnie dodać do siebie ich wyniki. ponieważ ponieważ Obliczanie logarytmów bardzo szczegółowo omówiłam w osobnym wpisie. Taką procedurę stosujemy wtedy, gdy dodawane przez nas logarytmy mają różne podstawy - tak było w tym przypadku:
Mnożenie logarytmów o różnych podstawach Oblicz wartość wyrażenia x, y, z wykonując działania z mnożeniem logarytmów o różnych podstawach a następnie oblicz wartość wyrażenia A. Rozwiązanie: W podanych działaniach będziemy korzystać z następującego wzoru z mnożeniem logarytmów o różnych podstawach: Wzór na zmianę podstawy logarytmu. Stosując następującą metodę możemy zamienić podstawę dowolnego logarytmu: log b ( a) = log x ( a) log x ( b) Uwagi: Nowa podstawa, x. . , może mieć dowolną wartość. Jak zawsze, aby ten wzór był prawdziwy, argumenty logarytmów muszą być dodatnie a ich podstawy dodatnie i różne od 1. .

Ejercicios de unidades de medidas 1a by Gerson Villa Gonzalez Issuu
Zmiana podstawy logarytmu. gdzie. Zwróć uwagę, że c jest dowolną liczbą, która spełnia warunki logarytmu, czyli jest większa od zera i różna od 1. Pozatym możesz wybrać jako nową podstawę logarytmu dowolną liczbę, która ułatwi Ci obliczenia. Logarytmy jak każdą inną liczbę możemy dodawać, odejmować, mnożyć i dzielić. Gdy podstawa logarytmu jest taka sama to mamy na to konkretne wzory z których bardzo często bedziesz korzystał. Gdy podstawa jest inna to jest to troche bardziej skomplikowane i często trzeba trochę pogłówkować, aby znaleźć dobry sposób na.