Okrąg (koło) można wpisać w czworokąt wtedy i tylko wtedy, gdy sumy przeciwległych boków są sobie równe |AB| + |CD| = |AD| + |BC|. - wyznaczamy długość odcinków |BC|=|BD| korzystając z twierdzenia II, oraz długości odcinków |AE|, |EB| wiedząc, że podstawa dolna trapezu równoramiennego |AB|=a, podstawa górna |CD|=b NOWY KURS w sprzedaży. Przedstawiamy fragment Lekcji szóstej rozszerzonej: "Dowody w planimetrii". W tym filmiku omawiam dowód, w którym jeśli mamy w trapezie równoramiennym zadaną wysokość (pierwiastek z iloczynu długości podstaw), to w ten trapez można wpisać okrąg. Kurs Planimetria jest multimedialnym kursem edukacyjnym dla.

Jaki znak , = należy wstawić pomiędzy polami S tych figur płaskich
Okrąg wpisany w trapez równoramienny. Dowody w planimetrii. (Kurs Planimetria Szkoła Średnia) eTrapez 48.1K subscribers Subscribe 20 1.3K views 1 year ago Planimetria CAŁA PLANIMETRIA w. Mówimy też, że trapez jest wpisany w okrąg. Okrąg można opisać na trapezie wtedy i tylko wtedy, gdy sumy miar przeciwległych kątów są równe. Na każdym trapezie równoramiennym można opisać okrąg. Aby wyznaczyć środek okręgu opisanego na trapezie, należy wyznaczyć punkt przecięcia się symetralnych dwóch boków trapezu. Ważne! Czworokąt wypukły można wpisać w okrąg wtedy i tylko wtedy, gdy suma jego przeciwległych kątów jest równa 180 °, czyli gdy. α + γ = β + δ = 180 °. Czworokąt można wpisać w okrąg wtedy i tylko wtedy, gdy symetralne wszystkich jego boków przecinają się w jednym punkcie. Trapez równoramienny Jest to trapez, który posiada ramiona tej samej długości Miara przeciwległych kątów wynosi 180 ∘ ∘. Poza tym przekątne trapezu równoramiennego są jednakowej długości. Przykłady zadań Przykład 1: Oblicz wysokość trapezu o podstawach długości 14cm i 21cm i ramionach długości 6cm i 8cm.

Okrąg wpisany w trapez równoramienny. Fragment Lekcji 6 Dowody w
Rozwiązanie zadania: Na okręgu o promieniu 2,2cm opisano trapez równoramienny, którego ramię ma długość 5,7cm. Oblicz obwód. Suma miar kątów przy każdym ramieniu trapezu jest równa 180°. s α + β = 180° Na czworokącie można opisać okrąg, gdy suma jego przeciwległych kątów jest równa 180°. W dowolnym trapezi równoramiennym to właśnie zachodzi. α + β = 180° c.n.u. Strona matematykaszkolna.pl używa ciasteczek (cookies), dzięki którym działa lepiej. Trapez równoramienny - jak sama nazwa wskazuje, to taki trapez który ma dwa ramiona równej długości. a, b a, b - podstawy trapezu. c c - ramiona trapezu. h h - wysokość trapezu. e e - przekątna trapezu. Wzór na pole trapezu równoramiennego: P = 1 2(a + b) ⋅ h P = 1 2 ( a + b) ⋅ h. Obwód trapezu równoramiennego: Zadanie 15: trapez równoramienny, okrąg wpisany o promieniu r, obliczenie promienia okręgu opisanego na trapezie [1:44:13] Zadanie 16:. Zadanie 25: trapez prostokątny, okrąg wpisany w trapez, odległości środka okręgu od końców dłuższego ramienia, obwód trapezu [2:52:32] Zadanie 26: równoległobok, podany kąt ostry i.
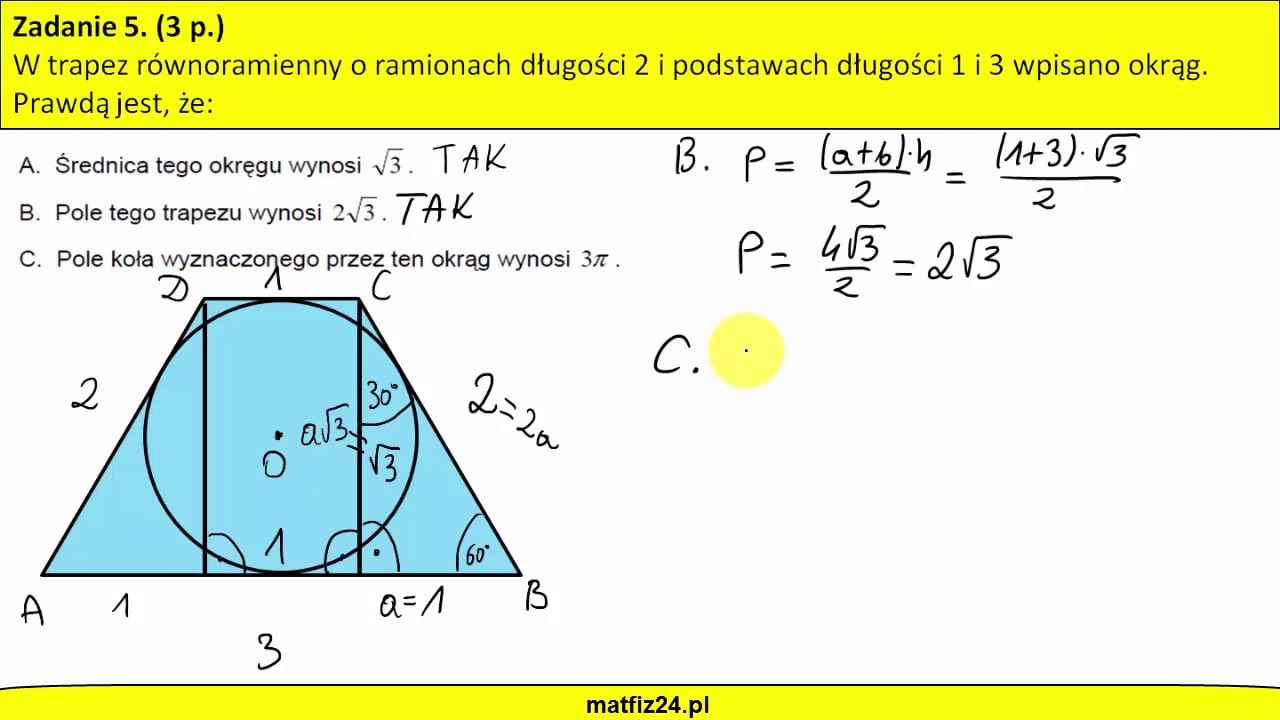
Własności trójkąta 30 60 90 w trapezie równoramiennym YouTube
Zadanie 6. (4 pkt) matura 2024 PR. W trapez prostokątny ABCD wpisano okrąg o środku O, który w punkcie P jest styczny do dłuższego ramienia BC tego trapezu (zobacz rysunek). Wykaż, że jeżeli |BP| = p i |CP| = q, to obwód trapezu jest równy 2( p-√ + q√)2. Film premium. Trapez jest czworokątem, który ma dwa boki równoległe. Na rysunku poniżej równoległe są boki a i b. Pole trapezu obliczamy ze wzoru: P = 1 2(a + b) ⋅ h. Zadanie 1. matura 2024 PP. W trapezie równoramiennym, który nie jest równoległobokiem, kąty przy ramieniu różnią się o 50∘. Kąt przy krótszej podstawie tego trapezu jest.
Długość promienia okręgu wpisanego w trapez równoramienny jest równa połowie długości wysokości tego trapezu. Rozwiązanie: Na okręgu opisano trapez (czyli w trapez wpisano okrąg). Kąt rozwarty trapezu ma miarę 150°, a odcinek łączący środki ramion tego trapezu ma długość 18cm. Zadanie polega na obliczeniu promienia. Jeśli teraz wyliczymy wysokość, będzie ona średnicą naszego okręgu. Żeby sobie zobrazować, narysuj trapez wraz z dwiema wysokościami. W trapezie równoramiennym wysokości te dzielą podstawę na 3 części, dwie skrajne są takiej samej długości natomiast środkowa ma długość podstawy a. Wyliczmy te skrajne, oznaczmy je jako x:

W trapez równoramienny wpisano okrąg .oblicz pole tego trapezu jeśli
Jeżeli czworokąt wpisany jest w okrąg, to prawdziwa jest następująca zależność: Przykład 1. Wykaż, że jeżeli na trapezie da się opisać okrąg, to jest on równoramienny. Wiemy, że na tym trapezie można opisać okrąg, zatem prawdziwa jest równość: W trapezie, suma miar kątów przy jednym ramieniu jest równa , dlatego: Aby. Udowodnij, że trapez równoramienny i trójkąt równoramienny wpisany w okrąg (koło) mają takie same pola powierzchni. Wiedząc, że dłuższa podstawa trapezu jest średnicą okręgu, a ramiona trójkąta są równolegle do ramion trapezu. Przekątna trapezu jest równa ramieniu trójkąta.




